Sóng hấp dẫn
| Thuyết tương đối rộng |
|---|
 |
|
Dẫn nhập · Lịch sử · Nguyên lý toán học Kiểm chứng |
|
Khái niệm cơ sở |
|
Hiệu ứng và hệ quả |
|
Lý thuyết phát triển |
|
Nhà vật lý Einstein · Lorentz · Hilbert · Poincare · Schwarzschild · Sitter · Reissner · Nordström · Weyl · Eddington · Friedman · Milne · Zwicky · Lemaître · Gödel · Wheeler · Robertson · Bardeen · Walker · Kerr · Chandrasekhar · Ehlers · Penrose · Hawking · Taylor · Hulse · Stockum · Taub · Newman · Khâu Thành Đồng · Thorne khác |

Trong vật lý học, sóng hấp dẫn (tiếng Anh: gravitational wave) là những dao động nhấp nhô bởi độ cong của cấu trúc không-thời gian thành các dạng sóng lan truyền ra bên ngoài từ sự thăng giáng các nguồn hấp dẫn (thay đổi theo thời gian), và những sóng này mang năng lượng dưới dạng bức xạ hấp dẫn. Albert Einstein, vào năm 1916,[1][2] dựa trên thuyết tương đối rộng của ông lần đầu tiên đã dự đoán có sóng hấp dẫn.[3][4] Nhóm cộng tác khoa học Advanced LIGO đã thu được trực tiếp tín hiệu sóng hấp dẫn từ kết quả hai lỗ đen sáp nhập vào ngày 14 tháng 9 năm 2015 và phát hiện này được thông báo trong cuộc họp báo tổ chức ngày 11 tháng 2 năm 2016 bởi Quỹ Khoa học Quốc gia (NSF).[5][6][7] Theo thuyết tương đối rộng, sóng hấp dẫn có thể phát ra từ một hệ sao đôi chứa sao lùn trắng, sao neutron hoặc lỗ đen. Hiện tượng sóng hấp dẫn là một trong những hệ quả của tính hiệp biến Lorentz cục bộ trong thuyết tương đối tổng quát, bởi vì tốc độ lan truyền tương tác bị giới hạn bởi đặc tính này. Nhưng trong lý thuyết hấp dẫn của Newton tất cả các vật tương tác tức thì với nhau, vì vậy không có sóng hấp dẫn trong lý thuyết cổ điển này.
Các nhà khoa học đã thăm dò dấu hiệu của bức xạ hấp dẫn bằng các phương pháp gián tiếp khác nhau. Ví dụ, Russell Hulse và Joseph Taylor tìm thấy hệ sao xung Hulse - Taylor có chu kỳ quỹ đạo giảm dần theo thời gian do hai sao neutron quay gần về phía nhau, từ đó cung cấp bằng chứng cho sự tồn tại của sóng hấp dẫn; vì sự phát hiện này mà vào năm 1993 hai ông được Giải Nobel Vật lý.[8] Các nhà khoa học cũng sử dụng các trạm dò sóng hấp dẫn để thám trắc hiệu ứng sóng hấp dẫn, ví dụ như Đài thám trắc sóng hấp dẫn - giao thoa kế laser (LIGO).
Giới thiệu[sửa | sửa mã nguồn]


Thuyết tương đối tổng quát của Einstein mô tả hấp dẫn là một hiện tượng gắn liền với độ cong của không-thời gian. Độ cong này xuất hiện vì sự có mặt của khối lượng. Càng nhiều khối lượng chứa trong một thể tích không gian cho trước, thì độ cong của không thời gian càng lớn hơn tại biên giới của thể tích này.[12] Khi vật thể có khối lượng di chuyển trong không thời gian, sự thay đổi độ cong hồi đáp theo sự thay đổi vị trí của vật. Trong một số trường hợp, vật thể chuyển động gia tốc gây nên sự thay đổi độ cong này mà lan truyền ra bên ngoài với tốc độ ánh sáng theo như dạng sóng. Hiện tượng lan truyền này được gọi là sóng hấp dẫn.[13][14]
Khi sóng hấp dẫn truyền tới một quan sát viên ở xa, bằng dụng cụ phát hiện người đó sẽ kết luận là không thời gian bị bóp méo. Khoảng cách giữa hai vật tự do sẽ biến đổi tăng giảm một cách nhịp nhàng (dao động), bằng với tần số của sóng hấp dẫn. Tuy nhiên, trong quá trình này, các vật là tự do và không có lực tác động giữa chúng, vị trí tọa độ là không thay đổi, sự thay đổi ở đây là thay đổi hệ tọa độ không gian và thời gian của khoảng cách giữa chúng. Đối với quan sát viên ở xa, cường độ sóng hấp dẫn tại vị trí của người này tỉ lệ nghịch với khoảng cách từ anh ta đến nguồn sóng.[14] Theo dự đoán của lý thuyết, ở các hệ sao đôi chứa sao neutron chuyển động vòng xoắn ốc vào nhau với tốc độ lớn trên quỹ đạo elip dẹt, chúng sẽ sáp nhập vào nhau trong tương lai và là nguồn phát ra sóng hấp dẫn mạnh. Nhưng bởi vì khoảng cách thiên văn đến chúng quá lớn, cho nên ngay cả các sóng hấp dẫn có cường độ cao nhất phát từ các sự kiện trong vũ trụ khi lan tới Trái Đất đã yếu đi rất nhiều, với biên độ dao động khoảng cách giữa hai vật thử thấp hơn 10−21.[15] Để phát hiện sự thay đổi tinh tế này, các nhà khoa học phải tìm cách tăng độ nhạy của máy dò. Tính đến năm 2012, các máy dò nhạy nhất nằm ở các trạm thám trắc LIGO và VIRGO có độ chính xác lên tới 5 x 10−22.[16] Các nhà vật lý đã tính toán ra ngưỡng giới hạn trên của tần số của sóng hấp dẫn lan truyền tới Trái Đất.[17][18] Cơ quan Vũ trụ châu Âu đang phát triển một hệ thống vệ tinh thám trắc trong không gian để phát hiện sóng hấp dẫn, tên dự án là Ăngten giao thoa kế Laser trong Vũ trụ (Laser Interferometer Space Antenna LISA).[19]
Sóng hấp dẫn có thể thâm nhập vào các vùng không gian mà sóng điện từ không thể xâm nhập. Dựa vào các tính chất thu được từ sóng hấp dẫn có thể giúp tìm hiểu Vũ trụ tại những vùng sâu nơi một số loại thiên thể kỳ lạ nằm ở đó, chẳng hạn như các cặp lỗ đen. Những đối tượng như vậy không thể quan sát trực tiếp theo cách truyền thống bằng kính thiên văn quang học và kính thiên văn vô tuyến. Ưu điểm này của sóng hấp dẫn cũng là một lợi thế để nghiên cứu trạng thái sớm nhất của Vũ trụ. Không thể áp dụng các phương pháp quan sát hiện nay bởi vì trước giai đoạn tái kết hợp electron, Vũ trụ trở lên mờ đục đối với toàn bộ dải sóng điện từ.[20] Ngoài ra, các phép đo chính xác hơn của sóng hấp dẫn có thể tiếp tục xác minh thuyết tương đối tổng quát.[14]
Sóng hấp dẫn về mặt lý thuyết có thể tồn tại ở bất kỳ tần số nào, nhưng hầu như không thể phát hiện được chúng ở tần số rất thấp, và nguồn phát sóng tần số cao được biết đến là không thể quan sát được. Stephen Hawking và Werner Isreal dự đoán rằng có thể phát hiện sóng hấp dẫn với tần số trong miền 10 -7 Hz tới 10 11 Hz.[21] Sóng hấp dẫn GW150914 mà nhóm hợp tác LIGO lần đầu tiên thu nhận trực tiếp có tần số trong khoảng 35 Hz đến 250 Hz.[7]
Các hiệu ứng khi sóng hấp dẫn truyền qua[sửa | sửa mã nguồn]
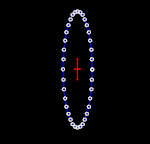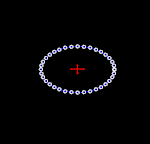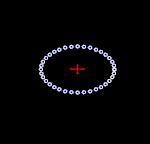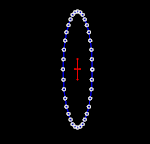
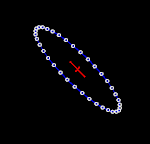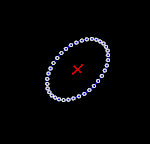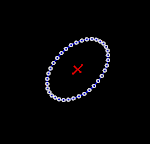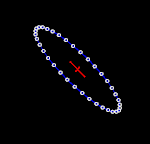
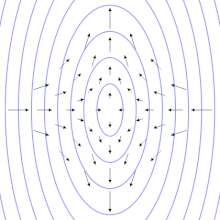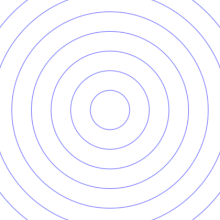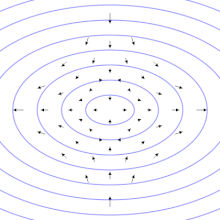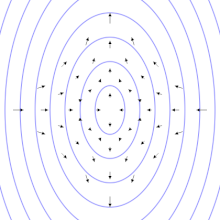
Để hiểu được tính chất của sóng hấp dẫn bằng cách thăm dò, có thể tưởng tượng trong một khu vực không-thời gian phẳng có một tập hợp các hạt thử đứng yên tạo thành một bề mặt phẳng. Khi sóng hấp dẫn truyền theo phương vuông góc với mặt phẳng này đi qua các hạt nó kéo giãn không gian và thời gian theo một hướng và nén không gian và thời gian theo hướng vuông góc (ảnh động bên phải). Diện tích bao quanh bởi các hạt thử nghiệm là không thay đổi, và các hạt không dịch chuyển theo hướng chuyển động của sóng (tức là chúng không bật ra khỏi bề mặt phẳng).[22]:209-210 Khi khoảng cách giữa các hạt theo phương dọc là lớn nhất thì khoảng cách giữa các hạt theo phương ngang là nhỏ nhất và ngược lại khoảng thời gian di chuyển giữa hai hạt theo phương ngang là lớn nhất và theo phương dọc là ít nhất.[14]
Hai hình bên cạnh minh họa phóng đại sự dao động của các hạt vì biên độ sóng hấp dẫn thực sự là rất nhỏ. Tuy nhiên chúng cho phép hình dung ra kiểu dao động đặc trưng của sóng hấp dẫn phát ra từ hai vật thể quay trên quỹ đạo hình tròn. Trong trường hợp này, biên độ của sóng hấp dẫn không thay đổi, nhưng mặt phẳng phân cực (hay phương dao động) thay đổi hay quay với chu kỳ bằng hai lần chu kỳ quỹ đạo của hai vật thể trong nguồn. Do đó, kích thước của sóng hấp dẫn (biến dạng tuần hoàn của không thời gian) thay đổi theo thời gian, như thể hiện trong các hình ảnh động.[23] Nếu quỹ đạo của hai vật thể là hình elip, thì biên độ của sóng hấp dẫn cũng sẽ thay đổi theo thời gian như được miêu tả bằng công thức tứ cực của Einstein.[2]
Giống như các sóng khác, sóng hấp dẫn có một số đặc điểm sau:[22]:203-204
- Biên độ: Thường được ký hiệu bằng , đại lượng này biểu thị độ lớn của sóng — phần bị dãn ra hay nén lại trong ảnh động.[24][Ct 1] Biên độ minh họa ở đây có giá trị gần bằng (hay 50%). Sóng hấp dẫn đi qua Trái Đất có biên độ nhỏ hơn hàng tỷ nghìn tỷ lần minh họa này — .[15] Chú ý rằng đại lượng này không giống với cái gọi là biên độ như của sóng điện từ, mà bằng . Các nhà vật lý thường dùng h với ý nghĩa là biến dạng của sóng hấp dẫn (gravitational wave strain).
- Tần số: Thường ký hiệu bằng f, đây là tần số mà sóng dao động (1 chia cho lượng thời gian giữa hai lần giãn và nén liên tiếp)
- Bước sóng: Thường ký hiệu bằng , đây là khoảng cách dọc theo phương truyền sóng giữa hai điểm có độ dãn hoặc độ nén lớn nhất.
- Tốc độ: Đây là tốc độ mà tại một điểm trên sóng (ví dụ, điểm tại độ giãn hay độ nén là lớn nhất) lan truyền. Đối với sóng hấp dẫn có biên độ nhỏ, tốc độ này bằng tốc độ ánh sáng, .[14]
Từ những đại lượng trên có thể tính toán ra độ sáng của sóng hấp dẫn bằng cách tính đạo hàm bậc ba theo thời gian đối với công thức tứ cực.[14]
Tốc độ, bước sóng, và tần số của sóng hấp dẫn có liên hệ với nhau bởi phương trình c = λ f, giống như phương trình của sóng ánh sáng. Ví dụ, ảnh động minh họa ở đây sóng hấp dẫn dao động động khoảng 1 lần trong 2 giây. Tương ứng với sóng này có tần số 0,5 Hz, và bước sóng vào khoảng 600.000 km, hay 47 lần đường kính Trái Đất.
Trong ví dụ vừa nêu, chúng ta đã giả sử một số điều đặc biệt về sóng. Chúng ta giả sử rằng sóng hấp dẫn là phân cực tuyến tính, hay phân cực "cộng", viết là . Sự phân cực của sóng hấp dẫn giống như phân cực của sóng ánh sáng ngoại trừ rằng sóng hấp dẫn phân cực ở góc 45 độ, như ngược lại đối với 90 độ. Đặc biệt, nếu chúng ta có sóng hấp dẫn phân cực "chéo", , hiệu ứng tác dụng lên các hạt thử về cơ bản là như nhau, nhưng góc quay đi 45 độ, như được chỉ ra ở hình thứ hai. Giống như phân cực ở sóng ánh sáng, sự phân cực ở sóng hấp dẫn cũng được biểu diễn theo kiểu sóng phân cực tròn. Sóng hấp dẫn bị phân cực bởi vì bản chất của nguồn phát ra chúng.[22]:209-210 Sự phân cực phụ thuộc vào góc từ nguồn, mà được trình bày ở phần tiếp theo.
Ước lượng giới hạn trên của biên độ[sửa | sửa mã nguồn]
Một hệ nguồn điển hình có các thành phần tứ cực với độ lớn , với M và R lần lượt là khối lượng và bán kính của hệ. Nếu chuyển động bên trong nguồn không có tính đối xứng cầu, thì đạo hàm bậc hai theo thời gian của thành phần tứ cực sẽ có độ lớn , trong đó là thành phần không đối xứng cầu của bình phương vận tốc bên trong nguồn phát ra sóng hấp dẫn. Khi thay vào công thức xác định biên độ sóng hấp dẫn từ các thành phần tứ cực ta có ước lượng biên độ[25]:đoạn 4.1.2
- .
Lưu ý ở đây là thế hấp dẫn Newton tại khoảng cách r nằm bên ngoài nguồn sóng, và tỉ số của biên độ sóng với thế hấp dẫn bên ngoài của nguồn tại khoảng cách r đến quan sát viên là
- .
Theo định lý virial đối với hệ hấp dẫn, tỷ số này không thể vượt quá giá trị lớn nhất của thế hấp dẫn Newton đối với bên trong nguồn sóng . Kết quả này rất thuận tiện và thiết thực đối với phương pháp ước tính giới hạn trên của biên độ sóng hấp dẫn. Đối với một sao neutron nằm trong cụm thiên hà ở chòm sao Xử Nữ thì biên độ bức xạ hấp dẫn nó phát ra có giới hạn trên xấp xỉ bằng 5×10-22. Trong hàng thập kỷ, các nhà khoa học đã sử dụng cách này để ước tính độ nhạy tối thiểu cho các máy dò sóng hấp dẫn phải bằng hoặc nhỏ hơn ×10-21.[25]:đoạn 4.1.2
Ước lượng tần số[sửa | sửa mã nguồn]
Trong một số trường hợp, tần số sóng hấp dẫn bị ảnh hưởng bởi chuyển động của nguồn, ví dụ, tần số của sóng hấp dẫn phát ra từ sao xung bằng hai lần tần số tự quay của ngôi sao.[25]:Đoạn 4.2.2 Nhưng đối với hầu hết các hệ thống sao đôi, tần số bức xạ hấp dẫn có liên quan đến tần số động lực tự nhiên của hệ hấp dẫn được định nghĩa là[25]:Đoạn 4.1.3[26]:Đoạn 2.1:
Ở đây là mật độ trung bình của khối lượng - năng lượng của nguồn sóng. Nó có cùng độ lớn với tần số quỹ đạo của hệ sao đôi (binary orbital frequency-tương đương với chu kỳ quỹ đạo) và tần số xung nhịp cơ bản (fundamental pulsation frequency) của vật thể.
Nếu ước lượng nguồn sóng phân bố trong mặt cầu với khối lượng M và bán kính R thì . Đối với một sao neutron có khối lượng 1,4 lần khối lượng Mặt Trời, bán kính bằng 10 km, tần số tự nhiên của nó sẽ là 1,9 kHz; đối với một lỗ đen có khối lượng 10 lần khối lượng của mặt trời, bán kính chân trời sự kiện bằng 30 km, tần số tự nhiên của nó bằng 1 kHz; và cho lỗ đen siêu khối lượng bằng 2,5 × 106 lần khối lượng của Mặt Trời, tần số tự nhiên của nó là 4 milliHertz, vì mật độ trung bình của nó thấp hơn.[25]:Đoạn 4.1.3 Nói chung, việc ước lượng tần số sóng hấp dẫn từ tần số tự nhiên của nguồn là đúng, về bản chất đó là một phương pháp thô cho phép ước lượng một cách nhanh chóng, cung cấp cho việc tính giá trị giới hạn trên của tần số đúng của nguồn sóng hấp dẫn.[27]:1
Nguồn sóng hấp dẫn[sửa | sửa mã nguồn]

Sóng hấp dẫn phát ra do sự không đối xứng của mô men tứ cực gây bởi chuyển động có gia tốc, với điều kiện là các chuyển động không hoàn toàn đối xứng cầu (giống như một quả cầu nở rộng hoặc co lại) hoặc đối xứng trụ (giống như một đĩa quay hoặc hình cầu quay quanh trục). Một ví dụ đơn giản của nguyên tắc này đó là trường hợp ở quả tạ quay. Nếu quả tạ quay tít như bánh xe trên một trục, nó sẽ không tỏa ra sóng hấp dẫn; nếu quay quanh trục như hai hành tinh quay quanh nhau, nó sẽ tỏa ra sóng hấp dẫn.[28]:149 Quả tạ càng nặng, và quay càng nhanh thì sóng hấp dẫn sẽ phát ra càng mạnh. Nếu chúng ta tưởng tượng một trường hợp cực hạn, trong đó hai đầu của quả tạ là những thiên thể lớn như sao neutron hoặc lỗ đen quay quanh nhau rất nhanh, thì một lượng đáng kể các bức xạ hấp dẫn sẽ phát ra từ hệ này.
Tần số sóng hấp dẫn phụ thuộc vào đặc trưng hệ động lực quy mô theo thời gian. Đối với hệ sao đôi, tần số quỹ đạo của hai thiên thể quay quanh nhau chính là tần số của sóng hấp dẫn mà hệ phát ra. Các nguồn sóng hấp dẫn thường được phân loại theo dải tần số. Tần số 1 Hz đến 10 kHz là dải nguồn sóng cao tần, như hệ hai sao neutron, hệ hai lỗ đen, siêu tân tinh... và đây cũng chính là dải tần mà các máy thăm dò sóng hấp dẫn trên mặt đất có thể phát hiện ra được. Từ 1mHz đến 1 Hz được phân loại thành nguồn sóng thấp tần, như lỗ đen siêu khối lượng, hệ hai sao lùn trắng... những nguồn này có thể phát hiện từ những vệ tinh quan trắc sóng hấp dẫn dựa trên phương pháp giao thoa kế laser để đo dịch chuyển Doppler của chùm tia laser. Nguồn sóng từ 1nHz đến 1mHz được phân loại thành dải tần rất thấp, từ các nguồn lỗ đen siêu khối lượng, dây vũ trụ... Phương pháp phát hiện sóng hấp dẫn bằng cách theo dõi cũng một lúc thời gian đến của xung sóng vô tuyến từ nhiều sao xung một lúc cho phép xác định sóng hấp dẫn trong phạm vi tần số rất nhỏ từ 10−18 Hz đến 10−15 Hz, tương ứng với sóng hấp dẫn phát ra từ thời điểm vũ trụ lạm phát sau Vụ Nổ Lớn mà những sóng này có thể để lại dấu vết trong bức xạ phông vi sóng vũ trụ.[28]:149-150
Hệ sao đôi[sửa | sửa mã nguồn]



Những hệ sao đôi có khả năng phát ra sóng hấp dẫn ở mức quan sát được bao gồm hệ chứa một sao lùn trắng, hoặc một sao neutron hoặc lỗ đen và các hệ sao đôi khoảng cách quỹ đạo giữa hai thiên thể là nhỏ, như hệ sao quay quanh một lỗ đen, hệ sao neutron quay quanh lỗ đen, hệ hai sao neutron, hệ hai sao lùn trắng... Những hệ này có thành phần mô men tứ cực với độ biến thiên theo thời gian lớn, và là những nguồn quan trọng đối với các trạm quan trắc trên mặt đất như LIGO và trạm thăm dò trong không gian như eLISA. Cho tới nay chỉ có những chứng cứ gián tiếp xác nhận sự tồn tại của sóng hấp dẫn thông qua việc quan sát những nguồn sóng này (chẳng hạn hệ sao xung và sao PSR 1913+ 16). Trên toàn bộ, quá trình bức xạ sóng hấp dẫn từ hệ sao đôi bao gồm quá trình ba giai đoạn, hai thiên thể quay xoáy ốc càng gần về nhau (inspiral) với tốc độ ngày càng nhanh hơn và càng gần nhau hơn, sáp nhập vào nhau (merger) tạo thành vật thể duy nhất quay xung quanh trục của nó một cách ổn định khi nó phát ra sóng hấp dẫn mang theo thông tin về khối lượng và spin của vật thể này (ringdown phase - giai đoạn rung ngân).[29]
Bức xạ hấp dẫn phát ra từ hệ sao đôi làm hệ mất mô men động lượng, khiến cho quỹ đạo của hệ suy giảm dần với một tốc độ rất chậm, dần dần làm cho hai thiên thể va chạm vào nhau. Nói cách khác, thời gian làm cho quỹ đạo của hệ suy giảm lớn hơn rất nhiều lần so với chu kỳ quỹ đạo của nó, do đó giai đoạn sáp nhập thường được tinh toán bằng phương pháp xấp xỉ hậu Newton dùng để tiên đoán ra dạng sóng hấp dẫn mà hệ sẽ phát ra.[30] Tần số sóng hấp dẫn có thể được suy ra từ phương pháp xấp xỉ, do tần số này tỉ lệ với căn bậc hai của mật độ trung bình của khối lượng - năng lượng của hệ đôi. Các trạm quan trắc mặt đất có thể phát hiện ra các hệ sao đôi neutron và lỗ đen khối lượng sao, trong khi eLISA được phát triển để thăm dò các hệ đôi sao lùn trắng và các lỗ đen siêu khối lượng khác.[25]:Đoạn 4.2.3[28]:149-150
Sóng hấp dẫn lấy đi năng lượng từ quỹ đạo khiến cho quỹ đạo của hệ hai thiên thể sẽ dần co lại, kết quả là tần số sóng hấp dẫn phát ra sẽ tăng theo thời gian, hay được gọi là tín hiệu di tần (chirp signal). Tín hiệu di tần có thể được theo dõi trong một khoảng thời gian dài, và chúng ta có thể tính được khối lượng của hệ hai thiên thể nhờ tín hiệu chirp[Ct 2], và từ kết quả quan trắc được biên độ sóng hấp dẫn ta sẽ thu được khoảng cách từ nguồn đến Trái Đất, và có nghĩa là phương pháp này sẽ bổ sung thêm một cách để đo hằng số Hubble và hằng số vũ trụ khác.[31]
Với bán kính quỹ đạo của hệ thiên thể đôi giảm tăng dần, phương pháp gần đúng đoạn nhiệt không còn được áp dụng, hệ tiến tới giai đoạn hai vật sáp nhập vào nhau: giai đoạn hai vật thể sáp nhập dữ dội tạo ra một lỗ đen mới, và một lượng đáng kể năng lượng và động lượng được giải phóng dưới dạng sóng hấp dẫn (nhưng ngoài ra phần lớn dạng mô men động lượng không bị sóng hấp dẫn mang đi bởi định luật bảo toàn mô men động lượng, điều này dẫn tới hình thành một đĩa bồi tụ xung quanh lỗ đen mới, đĩa bồi tụ vật chất sẽ phát ra các chớp tia gamma), phương pháp xấp xỉ Newton cũng không áp dụng được ở đây (xem lỗ đen khối lượng sao); sau cùng một lỗ đen hình thành trong trạng thái xoay quanh một trục với vận tốc xoay chậm dần, cùng với đó là tần số sóng hấp dẫn phát ra cũng giảm dần, và cuối cùng lỗ đen sẽ ổn định về dạng lỗ đen miêu tả bằng mêtric Kerr.[32]
Theo kết quả thống kê và mô hình lý thuyết, số lượng các hệ đôi sao neutron là tương đối hiếm trong Vũ trụ, và số lượng chúng có thể quan sát được nhỏ hơn so với số lượng hệ đôi chứa một sao neutron và một sao lùn trắng, và phổ biến hơn là hệ chứa hai sao lùn trắng với sóng hấp dẫn phát ra có tần số thấp (10−5 đến 10−1 Hz).[33] Những hệ hai sao lùn trắng chắc chắn sẽ nhiều hơn hệ hai sao neutron quay trên quỹ đạo chật nổi tiếng là PSR B1913 + 16. Điều này bởi vì hầu hết trong Vũ trụ chiếm đa số là các ngôi sao có khối lượng nhỏ và trung bình, và hầu hết chúng ở trong hệ sao đôi. Các nhà vật lý thiên văn ước lượng được rằng, eLISA có khả năng phát hiện ra hàng ngàn những hệ đôi sao lùn trắng này, với xác suất tìm thấy cao hơn so với khả năng tìm thấy các hệ đôi sao neutron của những trạm thăm dò mặt đất. Nhưng mặt khác, trong Ngân Hà có quá nhiều hệ đôi sao lùn trắng sẽ dẫn tới mức độ ồn trong tần số dưới 1 milli-hertz, và mức ồn nền này được gọi là "mức ồn gây hiểu nhầm", vì nó cao hơn mức độ ồn từ thiết bị của các vệ tinh eLISA,[34] nhưng mức ồn này lại không ảnh hưởng tới những tín hiệu thu từ các hệ có chứa lỗ đen. Các hệ hai sao lùn trắng nằm bên ngoài Ngân Hà có biên độ sóng hấp dẫn tới Trái Đất quá nhỏ, mặc dù khi ấy mức ồn từ những hệ như vậy có tần số ồn tới 1 Hz, và mức ồn này vẫn còn thấp hơn nhiều so với mức ồn từ thiết bị của LISA.[35]
Sao xung[sửa | sửa mã nguồn]

Đối với một sao neutron quay độc lập (hay pulsar đơn lẻ hoặc những vật thể đặc tương tự khác), để trở thành nguồn phát sóng hấp dẫn tuần hoàn (preriodic gravitational waves) hay sóng liên tục (continuous gravitational waves) thì phải tồn tại sự phân bố khối lượng ở dạng bất đối xứng cầu (hay tồn tại dòng khối lượng). Những nguyên nhân gây ra sự bất đối xứng này gồm hai loại sau đây:
Kịch bản đầu tiên gắn với cấu hình hình học bất đối xứng của nó, bao gồm các cơ chế:[36]
- Bản thân ngôi sao là một hình phỏng cầu đối xứng không hoàn hảo (như trường hợp PSR J1748-2446ad trong cụm sao cầu Terzan 5, sao xung quay nhanh nhất được biết đến với tốc độ 716 lần trong một giây)[37])
- Trục đối xứng của sao neutron không trùng với trục quay của nó, hoặc tương đương trục từ trường ngôi sao không trùng với trục quay (như ở PSR 1828-11[38])
- Quá trình bồi tụ vật chất gây ra sự phân bố khối lượng bất đối xứng (chẳng hạn ở những hệ sao đôi khối lượng nhỏ phát ra tia X, ví dụ như Cygnus X-1)
Sự phân bố khối lượng bất đối xứng trên lớp vỏ sao neutron hiện nay được ước lượng nhỏ hơn 10−5 khối lượng Mặt Trời. Ví dụ, LIGO ước lượng được giá trị giới hạn trên của độ dẹt elipsoid (ε) của nguồn sóng hấp dẫn từ sao xung PSR J2124-3358 không lớn hơn 1,1×10-7[39]. Từ điều này có thể ước tính được thời gian suy giảm chu kỳ tự quay của sao neutron gây bởi sóng hấp dẫn là rất lớn. Do vậy bức xạ hấp dẫn dường như không phải là nguyên nhân chính làm giảm xuống chu kỳ quay thực sự của chúng. Chẳng hạn, bên trong tinh vân Con Cua với sao xung còn trẻ PSR J0534+2200, sự bất đối xứng của sao này có giới hạn trên với ε < 3×10-4, và biên độ biến dạng sóng hấp dẫn phát ra từ nguồn này h < 2×10-25; đối với các sao xung miligiây già hơn độ dẹt này vào khoảng 10−9, và nếu đo từ khoảng cách 1parsec thì giá trị biên độ biến dạng thu được rất nhỏ cỡ 10−28. Mặc dù những biên độ điển hình này thấp hơn rất nhiều độ nhạy của LIGO, nhưng các dữ liệu thu được cho phép các nhà vật lý thu được kết quả tương quan tương ứng với giới hạn trên của tín hiệu sóng hấp dẫn phát ra từ sao xung.[40]。
Một kịch bản thứ hai tạo ra sự bất đối xứng nằm ở chế độ r (r-mode), một dạng dao động chất lưu xảy ra bên trong lòng sao neutron (còn gọi là sóng Rossby) do hiệu ứng Coriolis. Những chế độ này có thể không tồn tại ổn định đủ để dẫn tới hình thành sóng hấp dẫn dưới những điều kiện thiên văn vật lý thực tế. Đối với trường hợp này, tính toán lý thuyết cho kết quả tần số của sóng hấp dẫn phát ra bằng 4/3 tần số quay của sao xung.[41][42]
Xem thêm[sửa | sửa mã nguồn]
Chú thích[sửa | sửa mã nguồn]
- ^ Giả sử có hai đoạn nối ba vật rơi tự do xếp thành hình chữ L, biên độ sóng hấp dẫn được định nghĩa là tỷ lệ phần trăm giữa hiệu số sự thay đổi trong khoảng cách giữa hai vật trên cánh L với khoảng cách ban đầu ∆L/L. Biên độ và nguồn sóng tứ cực tỷ lệ với đạo hàm bậc hai.[14]
- ^ Khối lượng chirp được định nghĩa là[26]
- ,
Tham khảo[sửa | sửa mã nguồn]
- ^ Einstein, A (tháng 6 năm 1916). “Näherungsweise Integration der Feldgleichungen der Gravitation”. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin. part 1: 688–696.
- ^ a b Einstein, A (1918). “Über Gravitationswellen”. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin. part 1: 154–167. line feed character trong
|journal=tại ký tự số 21 (trợ giúp) - ^ Finley, Dave. “Einstein's gravity theory passes toughest test yet: Bizarre binary star system pushes study of relativity to new limits”. Phys.Org.
- ^ The Detection of Gravitational Waves using LIGO, B. Barish
- ^ Castelvecchi, Davide; Witze, Witze (ngày 11 tháng 2 năm 2016). “Einstein's gravitational waves found at last”. Nature News. doi:10.1038/nature.2016.19361. Truy cập ngày 11 tháng 2 năm 2016.
- ^ Cho, Adrian (ngày 11 tháng 2 năm 2016). “Gravitational waves, Einstein's ripples in spacetime, spotted for first time”. Science. doi:10.1126/science.aaf4041. Truy cập ngày 11 tháng 2 năm 2016.
- ^ a b B. P. Abbott (LIGO Scientific Collaboration and Virgo Collaboration) (2016). “Observation of Gravitational Waves from a Binary Black Hole Merger”. Physical Review Letters. 116 (6). arXiv:1602.03837. doi:10.1103/PhysRevLett.116.061102.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ “The Nobel Prize in Physics 1993”. Nobel Foundation. Truy cập ngày 7 tháng 7 năm 2015.
for the discovery of a new type of pulsar, a discovery that has opened up new possibilities for the study of gravitation
- ^ Staff (ngày 17 tháng 3 năm 2014). “BICEP2 2014 Results Release”. National Science Foundation. Truy cập ngày 18 tháng 3 năm 2014.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ Clavin, Whitney (ngày 17 tháng 3 năm 2014). “NASA Technology Views Birth of the Universe”. NASA. Truy cập ngày 17 tháng 3 năm 2014.
- ^ Overbye, Dennis (ngày 17 tháng 3 năm 2014). “Detection of Waves in Space Buttresses Landmark Theory of Big Bang”. New York Times. Truy cập ngày 17 tháng 3 năm 2014.
- ^ Bản mẫu:Cite serial
- ^ Riles, K. (2013). “Gravitational waves: sources, detectors and searches”. Progress in Particle & Nuclear Physics. 68. arXiv:1209.0667v3.
- ^ a b c d e f g Kokkotas, Kostas D. (2002), “Gravitational wave physics”, Encyclopedia of Physical Science and Technology, 7 (ấn bản 3), Academic Press, tr. 67–85, ISBN 978-0-12-227410-7
- ^ a b Saulson, Peter R. (1998), Physics of gravitational wave detection: resonant and interferometric detectors (PDF), Syracuse, New York: XXVI SLAC Summer Institute on Particle Physics
- ^ LIGO Scientific Collaboration; Virgo Collaboration (2012). “Search for Gravitational Waves from Low Mass Compact Binary Coalescence in LIGO's Sixth Science Run and Virgo's Science Runs 2 and 3”. Physical Review D. 85: 082002. arXiv:1111.7314. Bibcode:2012PhRvD..85h2002A. doi:10.1103/PhysRevD.85.082002.
- ^ LIGO Scientific Collaboration; Virgo Collaboration (2012). “All-sky search for gravitational-wave bursts in the second joint LIGO-Virgo run”. Physical Review D. 85: 122007. arXiv:1202.2788. Bibcode:2012PhRvD..85l2007A. doi:10.1103/PhysRevD.85.122007.
- ^ LIGO Scientific Collaboration; Virgo Collaboration (2013). “Search for gravitational waves from binary black hole inspiral, merger, and ringdown in LIGO-Virgo data from 2009-2010”. Physical Review D. 87: 022002. arXiv:1209.6533. Bibcode:2013PhRvD..87b2002A. doi:10.1103/PhysRevD.87.022002.
- ^ “eLISA, The First Gravitational Wave Observatory in Space”. eLISA Consortium. Bản gốc lưu trữ ngày 5 tháng 12 năm 2013. Truy cập ngày 14 tháng 2 năm 2016.
- ^ Krauss, LM; Dodelson, S; Meyer, S (2010). “Primordial Gravitational Waves and Cosmology”. Science. 328 (5981): 989–992. arXiv:1004.2504. Bibcode:2010Sci...328..989K. doi:10.1126/science.1179541. PMID 20489015.
- ^ Hawking, S. W. and Israel, W., General Relativity: An Einstein Centenary Survey, Cambridge University Press, Cambridge, 1979, 98.
- ^ a b c Bernard Schutz (ngày 14 tháng 5 năm 2009). A First Course in General Relativity. Cambridge University Press. ISBN 978-0-521-88705-2.
- ^ Landau, L. D. and Lifshitz, E. M., The Classical Theory of Fields. Fourth Revised English Edition, Pergamon Press., 1975, 356–357.
- ^ Sigg, Daniel, Gravitational Waves (PDF)
- ^ a b c d e f Bernard Schutz (1999). “Gravitational Waves Astronomy”. Classical and Quantum Gravity. 16: A131–A156. doi:10.1088/0264-9381/16/12A/307.
- ^ a b B. F. Schutz (1997). “Low-frequencies Sources of Gravitational Waves: A Tutorial” (PDF). Chú thích journal cần
|journal=(trợ giúp) - ^ Cole Miller. “Binary Sources of Gravitational Radiation” (PDF).
- ^ a b c Jolien D. E. Creighton; Warren G. Anderson (ngày 9 tháng 1 năm 2012). Gravitational-Wave Physics and Astronomy: An Introduction to Theory, Experiment and Data Analysis. John Wiley & Sons. ISBN 978-3-527-63604-4.
- ^ Lỗi chú thích: Thẻ
<ref>sai; không có nội dung trong thẻ ref có tênThreePhases - ^ Luc Blanchet, Thibault Damour and Bala R. Iyer (1995). “Gravitational waves from inspiralling compact binaries: Energy loss and waveform to second-post-Newtonian order”. Physical Review D. 51: 5360–5386. doi:10.1103/PhysRevD.51.5360.
- ^ B. F. Schutz (1986). “Determining the Hubble constant from gravitational wave observations”. Nature. 323: 310. doi:10.1038/323310a0.
- ^ S. Kobayashi and P. Miszaros (2003). “Gravitational Radiation from Gamma-Ray Burst Progenitors”. The Astrophysical Journal. 589: 861–870. doi:10.1086/374733.
- ^ Chris Belczynski (2006). Astrophysics of neutron star binaries Lưu trữ 2010-05-27 tại Wayback Machine 6th International LISA Symposium
- ^ Leor Barack and Curt Cutler (2004). “Confusion noise from LISA capture sources”. Physical Review D. 70: 122002. doi:10.1103/PhysRevD.70.122002.
- ^ Cole Miller. “Binary Sources of Gravitational Radiation” (PDF). Astrophysics of GW Sources, Gravitational Wave Astronomy Summer School 2006. Bản gốc (PDF) lưu trữ ngày 4 tháng 3 năm 2016. Truy cập ngày 8 tháng 10 năm 2015.
- ^ The LIGO Scientific Collaboration (2007). “Coherent searches for periodic gravitational waves from unknown isolated sources and Scorpius X-1: results from the second LIGO science run”. 76. Phys.Rev.D. arXiv:gr-qc/0605028. doi:10.1103/PhysRevD.76.082001. Chú thích journal cần
|journal=(trợ giúp) - ^ Jason W. T. Hesselstitle=A Radio Pulsar Spinning at 716 Hz (2006). Science. 311: 5769 1901-1904. arXiv:astro-ph/0601337. doi:10.1126/science.1123430 http://www.sciencemag.org/cgi/content/abstract/311/5769/1901.
|title=trống hay bị thiếu (trợ giúp) - ^ Akgün, T., Link, B., & Wasserman, I. (2006). “Precession of the isolated neutron star PSR B1828-11”. MNARS. 365: 653–672. arXiv:astro-ph/0506606. doi:10.1111/j.1365-2966.2005.09745.x.Quản lý CS1: nhiều tên: danh sách tác giả (liên kết)
- ^ “Status of LIGO” (PDF). Keita Kawabe. LIGO Caltech Collaboration. 2007.
- ^ B. Abbott LIGO Scientific Collaboration (2007). “Upper limits on gravitational wave emission from 78 radio pulsars”. Physical Review D. 76 (4): 042001. arXiv:gr-qc/0702039. doi:10.1103/PhysRevD.76.042001.
- ^ L. Lindblom, B. J. Owen and S. M. Morsink (1998). “Gravitational Radiation Instability in Hot Young Neutron Stars”. Physical Review Letters. 80: 4843–4846. doi:10.1103/PhysRevLett.80.4843.
- ^ J. Papaloizou and J.E. Pringle (1978). “Non-radial oscillations of rotating stars and their relevance to the short-period oscillations of cataclysmic variables”. Mon. Not. R. Astro. Soc. 182: 423.
Đọc thêm[sửa | sửa mã nguồn]
- Chakrabarty, Indrajit, "Gravitational Waves: An Introduction". arXiv:physics/9908041 v1, Aug 21, 1999.
- Landau, L. D. and Lifshitz, E. M., The Classical Theory of Fields (Pergamon Press),(1987).
- Will, Clifford M., The Confrontation between General Relativity and Experiment. Living Rev. Relativity 9 (2006) 3.
- Peter Saulson, "Fundamentals of Interferometric Gravitational Wave Detectors", World Scientific, 1994.
- J. Bicak, W.N. Rudienko, "Gravitacionnyje wolny w OTO i probliema ich obnarużenija", Izdatielstwo Moskovskovo Universitieta, 1987.
- A. Kułak, "Electromagnetic Detectors of Gravitational Radiation", PhD Thesis, Cracow 1980 (In Polish).
- P. Tatrocki, "On intuitive description of graviton detector", www.philica.com.
- P. Tatrocki, "Can the LIGO, VIRGO, GEO600, AIGO, TAMA, LISA detectors really detect?", www.philica.com.
Thư mục tham khảo[sửa | sửa mã nguồn]
- Berry, Michael, Principles of cosmology and gravitation (Adam Hilger, Philadelphia, 1989). ISBN 0-85274-037-9
- Collins, Harry, Gravity's Shadow: the search for gravitational waves, University of Chicago Press, 2004.
- P. J. E. Peebles, Principles of Physical Cosmology (Princeton University Press, Princeton, 1993). ISBN 0-691-01933-9.
- Wheeler, John Archibald and Ciufolini, Ignazio, Gravitation and Inertia (Princeton University Press, Princeton, 1995). ISBN 0-691-03323-4.
- Woolf, Harry, ed., Some Strangeness in the Proportion (Addison–Wesley, Reading, Massachusetts, 1980). ISBN 0-201-09924-1.
Liên kết ngoài[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Sóng hấp dẫn. |
- Gravitational waves tại Encyclopædia Britannica (tiếng Anh)
- Gravitational Waves trên chương trình In Our Time của BBC. (Nghe tại đây)
- The LISA Brownbag Lưu trữ 2015-01-11 tại Wayback Machine – Selection of the most significant e-prints related to LISA science
- Astroparticle.org Lưu trữ [Date missing] tại Portuguese Web Archive. To know everything about astroparticle physics, including gravitational waves
- Caltech's Physics 237-2002 Gravitational Waves by Kip Thorne Lưu trữ 2006-07-21 tại Wayback Machine Video plus notes: Graduate level but does not assume knowledge of General Relativity, Tensor Analysis, or Differential Geometry; Part 1: Theory (10 lectures), Part 2: Detection (9 lectures)
- www.astronomycast.com ngày 14 tháng 1 năm 2008 Episode 71: Gravitational Waves
- Laser Interferometer Gravitational Wave Observatory. LIGO Laboratory, operated by the California Institute of Technology and the Massachusetts Institute of Technology
- The LIGO Scientific Collaboration
- Einstein's Messengers Lưu trữ 2014-02-09 tại Wayback Machine – The LIGO Movie by NSF
- Home page for Einstein@Home project, a distributed computing project processing raw data from LIGO Laboratory, searching for gravitational waves
- The National Center for Supercomputing Applications Lưu trữ 2009-05-21 tại Wayback Machine – a numerical relativity group
- Caltech Relativity Tutorial Lưu trữ 2014-05-30 tại Wayback Machine – A basic introduction to gravitational waves, and astrophysical systems giving off gravitational waves
- Resource Letter GrW-1: Gravitational waves – a list of books, journals and web resources compiled by Joan Centrella for research into gravitational waves
- Mathematical and Physical Perspectives on Gravitational Radiation Lưu trữ 2015-08-15 tại Wayback Machine – written by B F Schutz of the Max Planck Institute explaining the significance and background of some key concepts in gravitational radiation
- Binary BH Merger – estimating the radiated power and merger time of a BH binary using dimensional analysis





























