Hoàng đạo
Hoàng đạo hay mặt phẳng hoàng đạo là đường đi biểu kiến của Mặt Trời trên thiên cầu.[1][2] Các nhà thiên văn cũng xét đến mặt phẳng chứa hoàng đạo, nó đồng phẳng với quỹ đạo của Trái Đất quanh Mặt Trời (và do vậy trở thành quỹ đạo biểu kiến của Mặt Trời quanh Trái Đất). Đường đi của Mặt Trời thường ít được chú ý tới khi nhìn từ bề mặt Trái Đất do sự tự quay của Trái Đất, từ mang theo góc nhìn của người quan sát trên Trái Đất đi qua chu trình Mặt Trời mọc và Mặt Trời lặn, làm cản trở chuyển động biểu kiến của Mặt Trời so với các ngôi sao. Hoàng đạo là một mặt phẳng tham chiếu quan trọng và là cơ sở của hệ tọa độ hoàng đạo.

Chuyển động biểu kiến của Mặt Trời[sửa | sửa mã nguồn]
Chuyển động miêu tả ở trên là những cách đơn giản so với chuyển động thực tế. Do chuyển động của Trái Đất xung quanh khối tâm của hệ Trái Đất - Mặt Trăng, đường đi biểu kiến của Mặt Trời hơi đu đưa một chút, với chu kỳ vào khoảng một tháng. Cũng do các nhiễu loạn ảnh hưởng bởi các hành tinh khác trong hệ Mặt Trời, khối tâm hệ Trái Đất - Mặt Trăng hơi dao động xung quanh vị trí trung bình theo một cách phức tạp. Hoàng đạo thực sự là đường đi biểu kiến của Mặt Trời trong chu kỳ một năm.[3]
Do Trái Đất mất 1 năm quay quanh Mặt Trời, vị trí biểu kiến của Mặt Trời cũng mất cùng một khoảng thời gian để hoàn thành một vòng quanh hoàng đạo. Với một năm có hơn 365 ngày một chút, Mặt Trời dịch chuyển khoảng ít hơn 1° về phía đông[4] sau mỗi ngày. Khi đứng từ Trái Đất, có thể phát hiện ra sự thay đổi nhỏ trong vị trí của Mặt Trời so với các ngôi sao (khi đứng hướng trực tiếp về phía bắc hoặc phía nam), thì sẽ thấy vị trí của Mặt Trời chậm hơn khoảng 4 phút so với hôm trước nếu như Trái Đất không quay quanh Mặt Trời; một ngày Trái Đất bằng 24 tiếng dài hơn 23 tiếng 56 phút của ngày sao (sidereal day). Tuy vậy, miêu tả vừa rồi chỉ là một cách giản lược, dựa trên giả thiết Trái Đất quay quanh Mặt Trời với vận tốc không đổi. Vận tốc thực của Trái Đất biến đổi khi nó quay quanh Mặt Trời trong một năm, do vậy tốc độ của Mặt Trời di chuyển trên hoàng đạo cũng biến đổi. Ví dụ, Mặt Trời nằm ở phía bắc của xích đạo thiên cầu trong 185 ngày của 1 năm, và ở phía nam trong 180 ngày.[5] Sự biến đổi của vận tốc quỹ đạo Trái Đất cần được tính đến trong phương trình thời gian.[6]
Mối quan hệ với xích đạo thiên cầu[sửa | sửa mã nguồn]

Bởi trục quay của Trái Đất không vuông góc với mặt phẳng quỹ đạo của nó, mặt phẳng xích đạo của Trái Đất không đồng phẳng với mặt phẳng hoàng đạo, mà nghiêng với nó một góc 23,4°, hay còn được biết đến là độ nghiêng của mặt phẳng hoàng đạo.[7] Nếu xích đạo được chiếu hướng ra ngoài thiên cầu, mà tạo thành xích đạo thiên cầu, nó cắt hoàng đạo tại hai điểm gọi là các điểm phân. Mặt Trời, trong quá trình chuyển động biểu kiến dọc theo hoàng đạo, sẽ cắt xích đạo thiên cầu tại những điểm này, một theo hướng từ nam đến bắc, một theo hướng ngược lại từ bắc đến nam.[4] Điểm cắt từ nam đến bắc được gọi là điểm xuân phân, hay còn gọi là điểm đầu tiên của Bạch Dương và điểm nút lên của hoàng đạo trên xích đạo thiên cầu.[8] Điểm cắt theo hướng từ bắc đến nam là điểm thu phân hoặc điểm nút xuống.
Hướng của trục quay của Trái Đất và xích đạo không cố định trong không gian vũ trụ, mà nó quay theo cực của hoàng đạo (ecliptic pole) với chu kỳ khoảng 26.000 năm, một quá trình mà các nhà thiên văn gọi là tiến động Mặt Trời - Mặt Trăng (lunisolar precession), do quá trình này ảnh hưởng chủ yếu bởi lực hấp dẫn của Mặt Trời và Mặt Trăng lên hình dáng không phải là hình cầu hoàn hảo của Trái Đất (Trái Đất phình ra tại xích đạo và dẹt hơn ở hai cực của nó). Do vậy, hoàng đạo cũng không phải là đường cố định. Nhiễu loạn hấp dẫn của các hành tinh khác trong hệ Mặt Trời gây ra một chuyển động nhỏ hơn trong quỹ đạo của Trái Đất, và do đó là hoàng đạo, hay quá trình tiến động hành tinh. Tác động tổng hợp của hai quá trình này được gọi là tiến động chung (general precession), và sự thay đổi vị trí của các điểm phân vào khoảng 50 giây cung (xấp xỉ 0°,014) trên một năm.[9]
Tuy vậy, miêu tả ở trên vẫn là sự giản lược. Chuyển động chu kỳ của Mặt Trăng và chuyển động tuần hoàn biểu kiến của Mặt Trời (mà thực sự là chuyển động của Trái Đất trên quỹ đạo) gây ra những dao động tuần hoàn biên độ nhỏ giai đoạn ngắn (short-term small-amplitude periodic oscillation) ở trục quay của Trái Đất, và do đó là xích đạo thiên cầu, một quá trình mà các nhà thiên văn học gọi là chương động.[10] Ảnh hưởng này cộng thêm thành phần vào vị trí của các điểm phân; các vị trí của xích đạo thiên cầu và điểm thu phân khi kể đến đầy đủ cả hiện tượng tiến động và chương động được gọi là xích đạo và điểm phân thực (true equator and equinox); trong khi vị trí không kể đến ảnh hưởng của chương động gọi là xích đạo và điểm phân trung bình (mean equator and equinox).[11]
Độ nghiêng của hoàng đạo[sửa | sửa mã nguồn]
Độ nghiêng của hoàng đạo là thuật ngữ được các nhà thiên văn học sử dụng cho sự nghiêng của mặt phẳng xích đạo Trái Đất với mặt phẳng hoàng đạo, hoặc tương đương góc của trục quay Trái Đất với trục vuông góc với mặt phẳng hoàng đạo. Góc này có giá trị bằng 23,4° và hiện nay giá trị này đang giảm dần 0,013 độ (47 giây cung) trên một trăm năm do ảnh hưởng nhiễu loạn của các hành tinh.[12]
Giá trị góc của độ nghiêng của hoàng đạo thu được bằng cách quan sát các chuyển động của Trái Đất và các hành tinh trong hệ Mặt Trời trong nhiều năm. Các nhà thiên văn lập ra những lịch thiên văn cơ sở mới (fundamental ephemeris) khi độ chính xác của các quan sát ngày được nâng cao và sự hiểu biết về các quá trình động lực được tăng cường, và từ những lịch thiên văn này nhiều giá trị thiên văn được rút ra, bao gồm độ nghiêng của hoàng đạo.
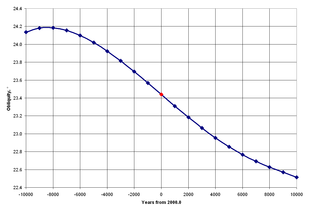
Cho đến năm 1983 độ nghiêng ở một ngày bất kỳ được tính toán dựa trên bảng vị trí các thiên thể của Simon Newcomb, nhà thiên văn đã phân tích vị trí các hành tinh cho đến tận năm 1895:
ε = 23° 27′ 08″.26 − 46″.845 T − 0″.0059 T2 + 0″.00181 T3
trong đó ε là độ nghiêng của hoàng đạo và T là thế kỷ chí tuyến từ kỷ nguyên B1900.0 cho đến ngày cần tìm giá trị trên bảng.[14]
Từ năm 1984, bộ lịch thiên văn DE do Phòng Thí nghiệm Sức đẩy Phản lực (JPL) lập ra bằng máy tính được sử dụng thay thế như là lịch thiên văn cơ bản của niên lịch Astronomical Almanac. Độ nghiêng hoàng đạo trong lịch DE200, mà dựa trên các quan sát từ năm 1911 đến 1979, được tính toán như sau:
ε = 23° 26′ 21″.45 − 46″.815 T − 0″.0006 T2 + 0″.00181 T3
với T là thế kỷ Julius từ kỷ nguyên J2000.0.[15]
Lịch thiên văn cơ sở của JPL liên tục được cập nhật. Ví dụ, giá trị độ nghiêng xác định trong Astronomical Almanac của năm 2010 là:[16]
ε = 23° 26′ 21″.406 − 46″.836769 T − 0″.0001831 T2 + 0″.00200340 T3 − 0″.576×10−6 T4 − 4″.34×10−8 T5
Các công thức trên cho độ nghiêng hoàng đạo có xu hướng tìm đến giá trị chính xác hơn trong một khoảng thời gian tương đối ngắn, có lẽ chỉ ± vài thế kỷ.[17] J. Laskar đã đưa ra một công thức biểu diễn đến độ lớn cỡ T10 với độ chính xác đến 0″.04/1000 năm trong 10.000 năm.[13]
Tất cả những công thức trên xác định cho độ nghiêng hoàng đạo trung bình, tức là bỏ qua ảnh hưởng của chương động thiên văn. Độ nghiêng thực hay độ nghiêng tức thời sẽ phải kể đến ảnh hưởng của chương động.[18]
Mặt phẳng của Hệ Mặt Trời[sửa | sửa mã nguồn]

|

|

|
| Nhìn theo phương chiếu đứng và chiếu cạnh của mặt phẳng hoàng đạo, với các hành tinh Sao Thủy, Sao Kim, Trái Đất, và Sao Hỏa. Hầu hết các hành tinh quay quanh Mặt Trời trong mặt phẳng rất gần với mặt phẳng quỹ đạo của Trái Đất, mặt phẳng hoàng đạo. | Bốn hành tinh sắp hàng trong tháng 7 năm 2010, minh họa cho mặt phẳng quỹ đạo của các hành tinh quay quanh Mặt Trời rất sát nhau. Bức ảnh chụp lúc hoàng hôn, nhìn về phía tây tại Surakarta, Java, Indonesia. | |
Phần lớn các thiên thể trong hệ Mặt Trời quay quanh Mặt Trời trong gần cùng một mặt phẳng. Nguyên nhân là do ban đầu hệ Mặt Trời hình thành từ một đĩa tiền hành tinh. Mặt phẳng biểu diễn gần sát nhất với đĩa này được gọi là mặt phẳng bất biến của hệ Mặt Trời. Quỹ đạo của Trái Đất, và do vậy là hoàng đạo, nghiêng một góc nhỏ hơn 1° so với mặt phẳng bất biến, và những hành tinh khác trong hệ Mặt Trời có mặt phẳng quỹ đạo của chúng nghiêng góc nhỏ hơn khoảng 6°. Vì vậy, hầu hết các vật thể trong hệ Mặt Trời nằm rất gần với hoàng đạo khi nhìn lên bầu trời. Hoàng đạo được định nghĩa theo bởi chuyển động của Mặt Trời. Mặt phẳng bất biến được định nghĩa theo mô men động lượng của toàn bộ hệ Mặt Trời, cơ bản đó là tổng của tất cả các vectơ mô men động lượng của tất cả các chuyển động trên quỹ đạo quanh Mặt Trời và sự quay quanh trục của chính mỗi vật thể, một giá trị đòi hỏi phải biết giá trị chính xác của mỗi vật thể trong hệ Mặt Trời. Vì lý do này, để cho thuận tiện, mặt phẳng hoàng đạo thường được sử dụng làm mặt phẳng tham chiếu cho hệ Mặt Trời.[19][20]
Mặt phẳng tham chiếu thiên cầu[sửa | sửa mã nguồn]

Hoàng đạo tạo thành một trong hai mặt phẳng cơ bản được dùng làm tham chiếu vị trí trên thiên cầu, mặt phẳng kia là xích đạo thiên cầu. Trục vuông góc với hoàng đạo xác định lên hai cực của hoàng đạo, cực bắc hoàng đạo là cực bắc của xích đạo. Trong hai mặt phẳng cơ bản này, mặt phẳng hoàng đạo ít thay đổi hơn so với các ngôi sao ở xa, chuyển động của nó so ảnh hưởng tiến động của các hành tinh chỉ gần bằng 1/100 so với của xích đạo thiên cầu.[21]
Biểu diễn bằng hệ tọa độ cầu, các hoàng kinh (kinh tuyến hoàng đạo) và hoàng vĩ (vĩ tuyến hoàng đạo) hoặc kinh tuyến và vĩ tuyến thiên cầu, được sử dụng để định vị trí trên thiên cầu so với mặt phẳng hoàng đạo. Giá trị kinh độ xác định dương theo hướng đông[4] từ 0° đến 360° dọc theo hoàng đạo từ điểm xuân phân, cùng hướng với hướng chuyển động của Mặt Trời. Vĩ độ được đo theo hướng vuông góc với hoàng đạo, đến +90° hướng về cực bắc hoặc -90° hướng về cực nam của hoàng đạo, hoàng đạo là vĩ tuyến được gán giá trị 0°. Một vị trí đầy đủ trên thiên cầu cũng cần tham số xác định khoảng cách. Các đơn vị khoảng cách khác nhau cũng được sử dụng cho những mục đích khác nhau. Bên trong hệ Mặt Trời, thường các nhà thiên văn học sử dụng đơn vị thiên văn, và đối với các vật thể gần Trái Đất, đơn vị bán kính Trái Đất hoặc kilômét được sử dụng. Hệ tọa độ trục vuông góc đặt ở góc phần tư thứ nhất cũng hay được sử dụng; với trục hoành x chỉ hướng về điểm xuân phân, trục tung vuông góc 90° y chỉ hướng về phía đông, và trục cao độ z' chỉ hướng về cực bắc hoàng đạo; đơn vị sử dụng là đơn vị thiên văn. Ký hiệu quy định chung cho hệ tọa độ hoàng đạo được sử dụng như ở bảng sau.[22]
| Tọa độ cầu | Vuông góc | |||
| Kinh độ | Vĩ độ | Khoảng cách | ||
| Địa tâm | λ | β | Δ | |
| Nhật tâm | l | b | r | x, y, z[note 1] |
| ||||
Sử dụng hệ tọa độ hoàng đạo thuận tiện nhất cho xác định vị trí các vật thể trong hệ Mặt Trời, vì hầu hết mặt phẳng quỹ đạo của các hành tinh nghiêng góc nhỏ so với mặt phẳng hoàng đạo, và do vậy chúng luôn xuất hiện rất gần với hoàng đạo trên bầu trời. Bởi quỹ đạo Trái Đất, và do đó là hoàng đạo, di chuyển rất ít, nên có thể coi như nó là mặt phẳng cố định so với các ngôi sao.

Do chuyển động tiến động của các điểm phân, tọa độ hoàng đạo của các vật thể trên thiên cầu liên tục thay đổi. Xác định một vị trí bên trong hệ tọa độ hoàng đạo đòi hỏi xác định theo một điểm phân cụ thể, nghĩa là điểm phân của một ngày cụ thể, được các nhà thiên văn định nghĩa là kỷ nguyên; tọa độ xác định hướng của điểm phân tại ngày đó. Ví dụ, bảng Astronomical Almanac[25] liệt kê các vị trí nhật tâm của Sao Hỏa lúc 0h giờ Trái Đất (Terrestrial Time), ngày 4 tháng 1 năm 2010 là: kinh độ 118° 09' 15".8, vĩ độ +1° 43' 16".7, khoảng cách thực đến Mặt Trời 1,6302454 AU, điểm phân trung bình và ngày hoàng đạo (mean equinox and ecliptic of date). Điều này xác định điểm phân trung bình của ngày 4 tháng 1 năm 2010 lúc 0h TT như miêu tả ở trên, mà không kể đến chương động.
Thiên thực[sửa | sửa mã nguồn]
Do mặt phẳng quỹ đạo của Mặt Trăng chỉ nghiêng khoảng 5,145° so với mặt phẳng hoàng đạo và Mặt Trời luôn nằm rất gần hoàng đạo, hiện tượng thiên thực luôn luôn xảy ra gần vị trí hoặc nằm trên hoàng đạo. Do quỹ đạo của Mặt Trăng nghiêng một góc nhỏ, thiên thực không xảy ra ở mỗi lần giao hội và xung đối giữa Mặt Trời và Mặt Trăng, mà chỉ khi Mặt Trăng nằm rất gần với điểm nút quỹ đạo lên hoặc điểm nút xuống trong cùng thời điểm nó ở vị trí giao hội hoặc xung đối với Mặt Trời. Người cổ đại cũng phát hiện ra hiện tượng thiên thực chỉ xảy ra khi đường đi của Mặt Trăng cắt qua hoàng đạo.[26]
Điểm phân và điểm chí[sửa | sửa mã nguồn]
| Hoàng đạo | Xích đạo | |
| Kinh độ | Xích kinh | |
| Xuân phân | 0° | 0h |
| Hạ chí | 90° | 6h |
| Thu phân | 180° | 12h |
| Đông chí | 270° | 18h |
Thời điểm chính xác của các điểm phân và điểm chí là lúc khi kinh độ hoàng đạo biểu kiến (bao gồm hiệu ứng quang sai và chương động) (hay hoàng kinh độ) của Mặt Trời là 0°, 90°, 180°, hoặc 270°. Do chuyển động trên quỹ đạo của Trái Đất bị ảnh hưởng nhiễu loạn và sự không đều khoảng thời gian ở lịch, ngày cho các điểm chí và điểm phân không cố định. [27]
Đi qua các chòm sao[sửa | sửa mã nguồn]
Trong thiên văn học hiện đại, Hoàng đạo hiện nay đi qua các chòm sao được liệt kê dưới đây:[28]
Chiêm tinh học[sửa | sửa mã nguồn]
Hoàng đạo tạo thành một đường trung tâm của một dải có độ rộng 20° gọi là cung Hoàng Đạo, mà Mặt Trời, Mặt Trăng và các hành tinh luôn chuyển động nằm trong dải này.[30] Trong chiêm tinh học, dải này được chia thành 12 phần có độ rộng 30° theo kinh tuyến, mỗi phần xấp xỉ với quãng đường Mặt Trời di chuyển trong một tháng.[31] Ở thời cổ đại, 12 phần này tương ứng với 12 chòm sao hoàng đạo.[32] Những thuật ngữ cho các phần này vẫn còn được sử dụng cho tới ngày nay. Điểm đầu tiên của Dương Cưu được đặt như vậy khi điểm xuân phân thực sự nằm trong chòm sao Bạch Dương; sau đó nó sẽ di chuyển đến Song Ngư.[33]
Xem thêm[sửa | sửa mã nguồn]
Tham khảo[sửa | sửa mã nguồn]
- ^ USNO Nautical Almanac Office; UK Hydrographic Office, HM Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. GPO. tr. M5. ISBN 978-0-7077-4082-9.
- ^ “LEVEL 5 Lexicon and Glossary of Terms”. caltech.edu. Truy cập 11 tháng 1 năm 2021.
- ^ U.S. Naval Observatory Nautical Almanac Office (1992). P. Kenneth Seidelmann (biên tập). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. ISBN 0-935702-68-7., tr. 11
- ^ a b c Các hướng bắc và nam trên thiên cầu được định nghĩa hướng về phía bắc của thiên cực bắc và hướng về phía nam của thiên cực nam. Hướng đông là hướng cùng chiều quay của trục Trái Đất, và hướng tây là hướng ngược lại.
- ^ Astronomical Almanac 2010, phần C
- ^ Explanatory Supplement (1992), phần 1.233
- ^ Explanatory Supplement (1992), tr. 733
- ^ Astronomical Almanac 2010, tr. M2 và M6
- ^ Explanatory Supplement (1992), phần 1.322 và 3.21
- ^ U.S. Naval Observatory Nautical Almanac Office; H.M. Nautical Almanac Office (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London., phần. 2C
- ^ Explanatory Supplement (1992), tr. 731 và 737
- ^ Chauvenet, William (1906). A Manual of Spherical and Practical Astronomy. I. J.B. Lippincott Co., Philadelphia. , art. 365-367, tr. 694-695 trên Google books
- ^ a b Laskar, J. (1986). “Secular Terms of Classical Planetary Theories Using the Results of General Relativity”., bảng 8, trên SAO/NASA ADS
- ^ Explanatory Supplement (1961), phần 2B
- ^ U.S. Naval Observatory, Nautical Almanac Office; H.M. Nautical Almanac Office (1989). The Astronomical Almanac for the Year 1990. U.S. Govt. Printing Office. ISBN 0-11-886934-5., tr. B18
- ^ Astronomical Almanac 2010, tr. B52
- ^ Newcomb, Simon (1906). A Compendium of Spherical Astronomy. MacMillan Co., New York., tr. 226-227 trên Google books
- ^ Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. ISBN 0-943396-35-2., chương. 21
- ^ Danby, J.M.A. (1988). Fundamentals of Celestial Mechanics. Willmann-Bell, Inc., Richmond, VA. ISBN 0-943396-20-4., phần 9.1
- ^ Roy, A.E. (1988). Orbital Motion . Institute of Physics Publishing. ISBN 0-85274-229-0., phần 5.3
- ^ Montenbruck, Oliver (1989). Practical Ephemeris Calculations. Springer-Verlag. ISBN 0-387-50704-3., phần 1.4
- ^ Explanatory Supplement (1961), phần 2A
- ^ Explanatory Supplement (1961), phần 1G
- ^ Dziobek, Otto (1892). Mathematical Theories of Planetary Motions. Register Publishing Co., Ann Arbor, Michigan., tr. 294 trên Google books
- ^ Astronomical Almanac 2010, tr. E14
- ^ Ball, Robert S. (1908). A Treatise on Spherical Astronomy. Đại học báo chí Cambridge. tr. 83. trên Google books
- ^ Meeus (1991), chương 26
- ^ Serviss, Garrett P. (1908). Astronomy With the Naked Eye. Harper & Brothers, New York and London. tr. 101. trên Google books
- ^ Serviss, Garrett P. (1908). Astronomy With the Naked Eye. Harper & Brothers, New York and London. tr. 105, 106. trên Google books
- ^ Bryant, Walter W. (1907). A History of Astronomy. tr. 3.
- ^ Bryant (1907), tr. 4.
- ^ See, for instance, Leo, Alan (1899). Astrology for All. tr. 8.
- ^ Vallado, David A. (2001). Fundamentals of Astrodynamics and Applications . El Segundo, CA: Microcosm Press. tr. 153. ISBN 1-881883-12-4.
Liên kết ngoài[sửa | sửa mã nguồn]
| Tra ecliptic hoặc Hoàng đạo trong từ điển mở tiếng Việt Wiktionary |
| Wikiversity tiếng Anh có tài liệu giáo dục và khoa học kỹ thuật về: Ecliptic |
- Hoàng đạo tại Từ điển bách khoa Việt Nam
- Ecliptic (astronomy) tại Encyclopædia Britannica (tiếng Anh)
- The Ecliptic: the Sun's Annual Path on the Celestial Sphere Hoàng đạo: Đường đi biểu kiến của Mặt Trời trên thiên cầu tại Khoa vật lý Đại học Durham.
- Các mùa và mô phỏng hoàng đạo tại Đại học Nebraska-Lincoln
- MEASURING THE SKY Hướng dẫn nhanh về thiên cầu của James B. Kaler, Đại học Illinois
- Các mùa của Trái Đất Lưu trữ 2007-10-13 tại Wayback Machine tại Trạm quan sát hải quân Hoa Kỳ
- Những khái niệm cơ bản – Hoàng đạo, Xích đạo và hệ thống tọa độ tại AstrologyClub.Org
- Kinoshita, H.; Aoki, S. (1983). “The definition of the ecliptic”. Celestial Mechanics. 31: 329–338. Bibcode:1983CeMec..31..329K. doi:10.1007/BF01230290.; đối chiếu các định nghĩa của LeVerrier, Newcomb và Standish.

