Các định lý đẳng cấu

Trong toán học, cụ thể hơn là trong đại số trừu tượng, các định lý đẳng cấu (hay còn được biết với tên các định lý đẳng cấu của Noether) là các định lý mô tả các mối quan hệ giữa thương, đồng cấu và vật con. Các định lý này có các phiên bản dành cho nhóm, vành, không gian vectơ, môđun, đại số Lie, và nhiều cấu trúc đại số khác. Trong đại số phổ dụng, các định lý đẳng cấu được tổng quát hóa dưới các đại số và các phép tương đẳng.

Lịch sử

Các định lý đẳng cấu được lần đầu viết thành công thức bởi Emmy Noether trong bài Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern, bài viết được xuất bản năm 1927 trong tạo chí Mathematische Annalen. Các phiên bản ít tổng quát hơn có thể được tìm thấy trong công trình của Richard Dedekind và các bài viết trước của Noether.

Ba năm sau, B.L. van der Waerden xuất bản cuốn sách trứ danh Moderne Algebra, cuốn sách này là sách đại số trừu tượng đầu tiên sử dụng hương tiếp cận nhóm-vành-trường cho chủ đề này. Van der Waerden ghi công các bài giảng của Noether trên lý thuyết nhóm và Emil Artin trên đại số, và chuyên đề được thực hiện bởi Artin, Wilhelm Blaschke, Otto Schreier, và chính van der Waerden tự ghi chính mình cho các ideal làm nguồn tham khảo chính.

Nhóm

Lưu ý về số thứ tự và tên

Dưới đây bốn định lý được đánh dấu lần lượt là A, B, C và D. Chúng thường được đánh thứ tự "Định lý đẳng cấu thứ nhất", "Định lý đẳng cấu thứ hai...", v.v; Tuy nhiên, không có thống nhất giữa tên gọi của các định lý đẳng cấu và mỗi tác giả có thể có cách đặt tên khác nhau. Để minh chứng, dưới đây là ví dụ của các tên gọi cho các đẳng cấu nhóm. Để ý rằng các định lý này cũng có phần tương tự khi xét vành và môđun.

So sánh tên của các định lý đẳng cấu trong lý thuyết nhóm

Tên gọi	Tác giả	Định lý A	Định lý B	Định lý C
Không có "Định lý đẳng cấu thứ ba"	Jacobson	Định lý nền tảng của các đồng cấu	(Định lý đẳng cấu thứ hai)	"hay được gọi là định lý đẳng cấu đầu tiên"
	van der Waerden, Durbin	Định lý nền tảng của các đồng cấu	Định lý đẳng cấu đầu tiên	Định lý đẳng cấu thứ hai
	Knapp	(Không tên)	Định lý đẳng cấu thứ hai	Định lý đẳng cấu đầu tiên
	Grillet	Định lý đồng cấu	Định lý đẳng cấu thứ hai	Định lý đẳng cấu đầu tiên
Xếp theo chữ số	(Cách gọi của Grillet)	Định lý đẳng cấu đầu tiên	Định lý đẳng cấu thứ ba	Định lý đẳng cấu thứ hai
	Rotman	Định lý đẳng cấu đầu tiên	Định lý đẳng cấu thứ hai	Định lý đẳng cấu thứ ba
	Fraleigh	(Không tên)	Định lý đẳng cấu thứ hai	Định lý đẳng cấu thứ ba
	Dummit & Foote	Định lý đẳng cấu đầu tiên	Định lý đẳng cấu thứ hai (hay Định lý hình thoi của đẳng cấu)	Định lý đẳng cấu thứ ba
Không có thứ tự	Milne	Định lý đồng cấu	Định lý đẳng cấu	Định lý tương ứng
	Scott	Định lý đồng cấu	Định lý đẳng cấu	Định lý năm nhất (hay định lý freshman)

Thường thì trong sách ít cho thêm định lý D, hay còn được gọi là định lý dàn, làm một trong các định lý đẳng cấu, nhưng khi cho thêm vào thì nó là cái cuối cùng.

Phát biểu các định lý

Định lý A (nhóm)

Xem thêm: Định lý nền tảng trên đồng cấu

Biểu đồ của định lý nền tảng trên các đồng cấu

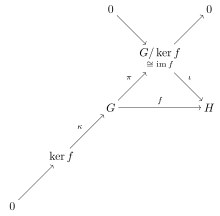
Đặt G và H là nhóm, và đặt f : G → H là đồng cấu nhóm. Khi đó:

1. Hạt nhân của f là nhóm con chuẩn tắc của G,
2. Ảnh của f là nhóm con của H, và
3. Ảnh của f đẳng cấu với nhóm thương G / ker(f).

Đặc biệt là, nếu f là toàn ánh thì H đẳng cấu với G / ker(f).

Định lý B (nhóm)

Biểu đồ cho định lý B3. Hai nhóm thương (trong hình nét đứt) đẳng cấu với nhau.

Đặt $G$ là nhóm . Gọi $S$ là nhóm con của $G$, và $N$ là nhóm con chuẩn tắc của $G$. Khi đó các mệnh đề sau được thỏa mãn:

1. Tích $SN$ là nhóm con của $G$,
2. Phần giao $S\cap N$ là nhóm con chuẩn tắc của $S$, và
3. Hai nhóm thương $(SN)/N$ và $S/(S\cap N)$ đẳng cấu với nhau.

Song,thực ra $N$ không cần thiết phải là nhóm con chuẩn tắc, chỉ cần $S$ là nhóm con của nhóm chuẩn hóa của $N$ trong $G$ là được. Trong trường hợp này, giao $S\cap N$ không phải nhóm con chuẩn tắc của $G$, nhưng nó vẫn là nhóm con chuẩn tắc của $S$.

Định lý này đôi khi được gọi là định lý đẳng cấu, định lý hình thoi hoặc định lý hình bình hành.

Một ứng dụng của định lý đẳng cấu thứ hai là dùng để xác định các nhóm tuyến tính xạ ảnh, ví dụ nhóm trên đường xạ ảnh phức bắt đầu bằng cách đặt $G=\operatorname {GL} _{2}(\mathbb {C} )$, nhóm của các ma trận phức khả nghịch kích thước 2 × 2, $S=\operatorname {SL} _{2}(\mathbb {C} )$, là nhóm con của các ma trận có định thức bằng 1, và $N$ là nhóm con chuẩn tắc của các ma trận scalar $\mathbb {C} ^{\times }\!I=\left\{\left({\begin{smallmatrix}a&0\\0&a\end{smallmatrix}}\right):a\in \mathbb {C} ^{\times }\right\}$, ta có $S\cap N=\{\pm I\}$, trong đó $I$ là ma trận đơn vị, và $SN=\operatorname {GL} _{2}(\mathbb {C} )$. Khi đó, từ định lý đẳng cấu thứ hai ta được:

$\operatorname {PGL} _{2}(\mathbb {C} ):=\operatorname {GL} _{2}\left(\mathbb {C} )/(\mathbb {C} ^{\times }\!I\right)\cong \operatorname {SL} _{2}(\mathbb {C} )/\{\pm I\}=:\operatorname {PSL} _{2}(\mathbb {C} )$

Định lý C (nhóm)

Gọi $G$ là nhóm và $N$ là nhóm con chuẩn tắc của $G$. Khi đó

1. Nếu $K$ là nhóm con của $G$ sao cho $N\subseteq K\subseteq G$, thì $G/N$ có nhóm con đẳng cấu với $K/N$.
2. Mọi nhóm con của $G/N$ có dạng $K/N$ cho một số nhóm $K$ của $G$ sao cho $N\subseteq K\subseteq G$.
3. Nếu $K$ là nhóm con chuẩn tắc của $G$ sao cho $N\subseteq K\subseteq G$, thì $G/N$ có nhóm con chuẩn tắc đẳng cấu với $K/N$.
4. Mọi nhóm con chuẩn tắc của $G/N$ có dạng $K/N$ cho một số nhóm con chuẩn tắc $K$ của $G$ sao cho $N\subseteq K\subseteq G$.
5. Nếu $K$ là nhóm con chuẩn tắc của $G$ sao cho $N\subseteq K\subseteq G$, thf nhóm thương $(G/N)/(K/N)$ đẳng cấu với $G/K$.

Định lý D (nhóm)

Bài chi tiết: Định lý dàn

Định lý tương ứng (hay còn được gọi là định lý dàn) đôi khi được gọi là định lý đẳng cấu thứ ba hoặc thứ tư.

Bổ đề Zassenhaus (hay còn gọi là bổ đề con bướm) đôi khi được gọi là định lý đẳng cấu thứ tự.

Vành

Phát biểu cho các vành cũng tương tự với nhóm, trong đó thay nhóm con chuẩn tắc bằng ideal.

Định lý A (vành)

Đặt R và S là vành và φ : R → S là đồng cấu vành. Khi đó:

1. Hạt nhân của φ là ideal của R,
2. Ảnh của φ là vành con của S, và
3. Ảnh của φ đẳng cấu với vành thương R / ker(φ).

Đặc biệt là, nếu φ là toàn ánh thì S đẳng cấu với R / ker(φ).

Định lý B (vành)

Đặt R là vành. Gọi S là vành con của R, và gọi I là ideal của R. Khi đó:

1. Tổng S + I = {s + i | s ∈ S, i ∈ I } là vành con của R,
2. Phần giao S ∩ I là ideal của S, và
3. Hai vành thương (S + I) / I và S / (S ∩ I) đẳng cấu với nhau.

Định lý C (vành)

Đặt R là vành, và I là ideal của R. Khi đó

1. Nếu $A$ là vành con của $R$ sao cho $I\subseteq A\subseteq R$, thì $A/I$ là vành con của $R/I$.
2. Mọi vành con của $R/I$ có dạng $A/I$ cho một số vành con $A$ của $R$ sao cho $I\subseteq A\subseteq R$.
3. Nếu $J$ là ideal của $R$ sao cho $I\subseteq J\subseteq R$, thì $J/I$ à ideal của $R/I$.
4. Mọi ideal của $R/I$ có dạng $J/I$ cho một số ideal $J$ của $R$ sao cho $I\subseteq J\subseteq R$.
5. Nếu $J$ là ideal của $R$ sao cho $I\subseteq J\subseteq R$, thì vành thương $(R/I)/(J/I)$ đẳng cấu với $R/J$.

Định lý D (vành)

Gọi $I$ là ideal của $R$.Phép tương ứng $A\leftrightarrow A/I$ là ánh xạ bảo toàn phép chứa giữa tập các vành con $A$ chứa $I$ của $R$ sang tập các vành con của $R/I$. Hơn nữa, $A$ (vành con chứa $I$) là ideal của $R$ khi và chỉ khi $A/I$ là ideal của $R/I$.

Môđun

Phát biểu của các định lý dành cho các môđun đơn giản hơn vì ta luôn thu được môđun thương từ bất kỳ môđun con. Các định lý đẳng cấu cho không gian vectơ (môđun trên một trường) và nhóm giao hoán (môđun trên $\mathbb {Z}$) là các trường hợp đặc biệt. Đối với các không gian vectơ hữu hạn số chiều, tất cả các định lý này đều có thể suy ra được từ định lý về hạng.

Dưới đây, từ "môđun" luôn có nghĩa "R-môđun" cho một số vành cố định R.

Định lý A (môđun)

Đặt M và N là môđun và φ : M → N là đồng cấu môđun. Khi đó:

1. Hạt nhân của φ là môđun con của M,
2. Ảnh của φ là môđun con của N, và
3. Ảnh của φ đẳng cấu với môđun thương M / ker(φ).

Đặc biệt là, nếu φ là toàn ánh thì N đẳng cấu với M / ker(φ).

Định lý B (môđun)

Đặt M là môđun, và đặt S và T là môđun con của M. Khi đó:

1. Tổng S + T = {s + t | s ∈ S, t ∈ T} là môđun con của M,
2. Phần giao S ∩ T là môđun con của M, và
3. Môđun thương (S + T) / T và S / (S ∩ T) đẳng cấu với nhau.

Định lý C (môđun)

Đặt M là môđun, T là môđun con của M.

1. Nếu $S$ là môđun con của $M$ sao cho $T\subseteq S\subseteq M$, then $S/T$ là môđun con của $M/T$.
2. Mọi môđun con of $M/T$ có dạng $S/T$ cho một số môđun con $S$ của $M$ sao cho $T\subseteq S\subseteq M$.
3. Nếu $S$ là môđun con of $M$ sao cho $T\subseteq S\subseteq M$, thì môđun thương $(M/T)/(S/T)$ đẳng cấu với $M/S$.

Định lý D (môđun)

Đặt $M$ là môđun, và $N$ là môđun con của $M$. Khi đó có song ánh giữa các môđun con của $M$ có chứa $N$ và các môđun con của $M/N$. Phép tương ứng được cho bởi $A\leftrightarrow A/N$ với mọi $A\supseteq N$. Phép tương ứng này giao hoán với quá trình lấy tổng và phần giao (tức là nó là đồng cấu dàn giữa dàn của các môđun con của $M/N$ và dàn của các môđun con $M$ có chứa $N$).

Đại số phổ dụng

Để tổng quát hóa sang đại số phổ dụng, các nhóm con chuẩn tắc cần phải được thay bằng các quan hệ tương đẳng.

Quan hệ tương đẳng (hay tương đẳng) trên đại số $A$ là quan hệ tương đương $\Phi \subseteq A\times A$ tạo đại số con của $A\times A$, đại số con này được coi là đại số đi cùng phép toán từng phần. Ta có thể biến tập của các lớp tương đương $A/\Phi$ thành một đại số có cùng kiểu qua các phép toán qua phần tử đại diện. Các phép toán này sẽ được định nghĩa tốt bởi bởi $\Phi$ là đại số con của $A\times A$. Cấu trúc thu về được được gọi là đại số thương.

Định lý A (đại số phổ dụng)

Gọi $f:A\rightarrow B$ là đồng cấu đại số. Khi đó ảnh của $f$ là đại số con của $B$, quan hệ cho bởi $\Phi :f(x)=f(y)$ (tức hạt nhân của $f$) tương đẳng trên $A$, và hai đại số $A/\Phi$ và $\operatorname {im} f$ đẳng cấu với nhau (Lưu ý rằng trong trường hợp nhóm, $f(x)=f(y)$ $\Leftrightarrow$ $f(xy^{-1})=1$, nên ta có thể tìm ra khái niệm của hạt nhân trong lý thuyết nhóm trong trường hợp này.)

Định lý B (đại số phổ dụng)

Cho đại số $A$, và đại số con $B$ của $A$, cùng với tương đẳng $\Phi$ trên $A$, gọi $\Phi _{B}=\Phi \cap (B\times B)$ là vết của $\Phi$ trong $B$ và $[B]^{\Phi }=\{K\in A/\Phi :K\cap B\neq \emptyset \}$ là họ các lớp tương đương giao với $B$. Khi đó

1. $\Phi _{B}$ là tương đẳng trên $B$,
2. $\ [B]^{\Phi }$ là đại số con của $A/\Phi$, và
3. Đại số $[B]^{\Phi }$ đẳng cấu với đại số $B/\Phi _{B}$.

Định lý C (đại số phổ dụng)

Cho$A$ là đại số và $\Phi ,\Psi$ là hai quan hệ tương đẳng trên $A$ sao cho $\Psi \subseteq \Phi$. Khi đó $\Phi /\Psi =\{([a']_{\Psi },[a'']_{\Psi }):(a',a'')\in \Phi \}=[\ ]_{\Psi }\circ \Phi \circ [\ ]_{\Psi }^{-1}$ tương đẳng trên $A/\Psi$, và $A/\Phi$ đẳng cấu với$(A/\Psi )/(\Phi /\Psi ).$

Định lý D (đại số phổ dụng)

Cho $A$ là đại số và đặt $\operatorname {Con} A$ là tập các tương đẳng trên $A$. Tập $\operatorname {Con} A$ là dàn đầy đủ sắp thứ tự theo phép chứa. Nếu $\Phi \in \operatorname {Con} A$ là tương đẳng và ta ký hiệu $\left[\Phi ,A\times A\right]\subseteq \operatorname {Con} A$ là tập tất cả các tương đẳng chứa $\Phi$ (tức là $\left[\Phi ,A\times A\right]$ là bộ lọc chính của $\operatorname {Con} A$, hơn nữa nó còn là dàn con), khi đo ánh xạ $\alpha :\left[\Phi ,A\times A\right]\to \operatorname {Con} (A/\Phi ),\Psi \mapsto \Psi /\Phi$ là đẳng cấu dàn.

Tham khảo

• Emmy Noether, Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern, Mathematische Annalen 96 (1927) pp. 26–61
• Colin McLarty, "Emmy Noether's 'Set Theoretic' Topology: From Dedekind to the rise of functors". The Architecture of Modern Mathematics: Essays in history and philosophy (edited by Jeremy Gray and José Ferreirós), Oxford University Press (2006) pp. 211–35.
• Jacobson, Nathan (2009), Basic algebra, 1 (ấn bản 2), Dover, ISBN 9780486471891
• Paul M. Cohn, Universal algebra, Chapter II.3 p. 57
• Milne, James S. (2013), Group Theory, 3.13
• van der Waerden, B. I. (1994), Algebra, 1 (ấn bản 9), Springer-Verlag
• Dummit, David S.; Foote, Richard M. (2004). Abstract algebra. Hoboken, NJ: Wiley. ISBN 978-0-471-43334-7.
• Burris, Stanley; Sankappanavar, H. P. (2012). A Course in Universal Algebra (PDF). ISBN 978-0-9880552-0-9.
• W. R. Scott (1964), Group Theory, Prentice Hall
• John R. Durbin (2009). Modern Algebra: An Introduction (ấn bản 6). Wiley. ISBN 978-0-470-38443-5.
• Anthony W. Knapp (2016), Basic Algebra
• Pierre Antoine Grillet (2007), Abstract Algebra (ấn bản 2), Springer
• Joseph J. Rotman (2003), Advanced Modern Algebra (ấn bản 2), Prentice Hall, ISBN 0130878685