Khác biệt giữa bản sửa đổi của “Logarit”

Nội dung được xóa Nội dung được thêm vào

Nội tuyến

Phiên bản lúc 15:55, ngày 17 tháng 6 năm 2020

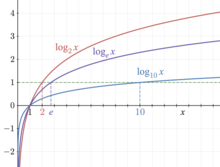
Trong toán học, logarit (tiếng Anh: logarithm) là hàm ngược của lũy thừa. Điều đó có nghĩa logarit của một số $x$ là số mũ mà một giá trị cố định, gọi là cơ số $b$ , phải được nâng lên lũy thừa để tạo ra số $x$ đó. Trong trường hợp đơn giản nhất, logarit là đếm số lần lặp đi lặp lại của phép nhân; ví dụ, vì $1000 = 10 \times 10 \times 10 = 10 3$ nên logarit cơ số $10$ của $1000$ là $3$ hay $log 10 (1000) = 3$ . Logarit cơ số $b$ của $x$ được ký hiệu là $log b (x)$ , $log b x$ hay $log x$ .

Tổng quát hơn, phép lũy thừa cho phép một số thực dương bất kỳ được nâng lên lũy thừa với một số mũ thực và kết quả thu được luôn là một số dương, do đó với hai số thực dương $b$ và $x$ bất kỳ, trong đó $b$ khác $1$ , $log b (x)$ luôn có giá trị bằng một số thực $y$ duy nhất. Một cách rõ ràng hơn, định nghĩa liên hệ giữa lũy thừa và logarit là:

\log _{b}(x)=y

khi và chỉ khi

\ b^{y}=x\

và

\ x>0

và

\ b>0

và

\ b\neq 1

.

Ví dụ, $log 2 64 = 6$ vì $26 = 64$ .

Logarit cơ số $10$ ( $b = 10$ ) được gọi là logarit thập phân và có nhiều ứng dụng trong khoa học và kỹ thuật. Logarit tự nhiên có cơ số là hằng số $e$ ( $b \approx 2,718$ ), được ứng dụng phổ biến nhất trong toán học và vật lý vì tích phân và đạo hàm của nó đơn giản hơn. Logarit nhị phân sử dụng cơ số $2$ ( $b = 2$ ) và được sử dụng nhiều nhất trong khoa học máy tính.^[1]

Logarit do John Napier giới thiệu lần đầu tiên vào năm 1614 như là một cách để đơn giản hóa việc tính toán.^[2] Về sau, nhiều nhà khoa học đã sử dụng nó để hỗ trợ trong tính toán, đặc biệt là các phép tính yêu cầu độ chính xác cao. Bằng cách sử dụng bảng số logarit, các phép nhân phức tạp với rất nhiều chữ số được thay bằng việc tra cứu bảng số và thực hiện các phép cộng đơn giản. Đó là vì logarit của một tích bằng tổng các logarit của các thừa số:

\log _{b}(xy)=\log _{b}x+\log _{b}y,\,

trong đó $b$ , $x$ và $y$ đều là số dương và $b \neq 1$ . Thước loga, vốn được dựa trên logarit, cho phép tính nhanh mà không cần bảng số nhưng với độ chính xác thấp hơn. Ký hiệu logarit như ngày nay đến từ Leonhard Euler, người đã liên hệ nó với hàm mũ vào thế kỷ 18 và cũng là người tìm ra chữ $e$ như là cơ số của logarit tự nhiên.^[3]

Thang đo logarit đưa các đại lượng mở về phạm vi nhỏ hơn. Chẳng hạn, decibel (dB) là đơn vị dùng để đưa tỷ lệ logarit, phần lớn cho công suất tín hiệu và biên độ (trong đó có áp suất âm thanh). Trong hóa học, pH là chỉ số logarit để đo độ axit hay bazơ của dung dịch nước. Logarit cũng phổ biến trong công thức khoa học, trong việc nghiên cứu độ phức tạp của tính toán hay các phân dạng. Nó hỗ trợ mô tả tỷ lệ tần số của các quãng trong âm nhạc, xuất hiện trong công thức đếm số nguyên tố hay tính gần đúng một giai thừa,...

Logarit phức là hàm ngược của hàm lũy thừa trong số phức. Một dạng khác của logarit là logarit rời rạc và có ứng dụng trong mật mã hóa khóa công khai.

Ý tưởng và định nghĩa

Phép cộng, phép nhân và lũy thừa là ba trong những phép toán cơ bản nhất. Phép ngược lại của phép cộng là phép trừ: nếu ta cộng thêm $5$ vào $x$ để có $x + 5$ , để đảo ngược thao tác này ta phải trừ $x + 5$ cho $5$ . Phép ngược lại của phép nhân là phép chia: nếu ta nhân $x$ cho $5$ để có $5 x$ thì sau đó, ta phải chia $5 x$ cho $5$ để có $x$ . Tương tự, logarit chính là phép toán ngược lại của lũy thừa. Lũy thừa là khi ta nâng một số lên một số mũ nhất định. Chẳng hạn, $2$ nâng lên lũy thừa $3$ bằng $8$ :

2^{3}=2\times 2\times 2=8

Trường hợp tổng quát là khi ta nâng một số $b$ lên lũy thừa $y$ để có $x$ :

b^{y}=x

Số $b$ ở đây được gọi là cơ số. Cơ số là số được nâng lên một số mũ nhất định, và trong ví dụ trên, cơ số này bằng $2$ . Để biểu diễn $b$ theo $x$ , ta lấy căn bậc $y$ cả hai vế để có:

b={\sqrt[{y}]{x}}

Biểu diễn $y$ theo $x$ khó hơn rất nhiều, nhưng logarit cho phép ta thực hiện điều này:

y=\log _{b}x

Biểu thức trên có nghĩa là $y$ là lũy thừa mà ta cần phải nâng $b$ lên để có được $x$ . Đây là phép ngược lại của lũy thừa vì logarit của $x$ cho ta biết được số mũ mà cơ số được nâng lên.

Lũy thừa

Đề mục con này tóm tắt ngắn gọn về phép lũy thừa, một bước cơ bản để hiểu được bản chất của logarit. Nâng $b$ lên lũy thừa $n$ , với $n$ là một số tự nhiên, tức là ta đã thực hiện phép nhân $n$ thừa số với nhau, mỗi thừa số bằng $b$ . Lũy thừa $n$ của $b$ được ký hiệu là $b n$ :

b^{n}=\underbrace {b\times b\times \cdots \times b} _{n}

Lũy thừa có thể được mở rộng thành dạng $b y$ , với $b$ là một số dương và số mũ $y$ là một số thực bất kỳ.^[4] Chẳng hạn $b -1$ là nghịch đảo của $b$ , hay bằng $1/ b$ . Nâng $b$ lên lũy thừa 1/2 thì được căn bậc hai của $b$ .

Tổng quát hơn, khi nâng $b$ lên lũy thừa hữu tỉ $p / q$ với $p$ và $q$ là số nguyên, ta có:

b^{p/q}={\sqrt[{q}]{b^{p}}},

hay căn bậc $q$ của $b^{p}\!\!$ .

Cuối cùng, mỗi số vô tỉ $y$ có thể được làm tròn để đưa về các số hữu tỉ. Sử dụng cách này, có thể tính được lũy thừa $y$ của $b$ : chẳng hạn ${\sqrt {2}}\approx 1,414...$ và $b^{\sqrt {2}}$ được tính gần đúng hơn theo dãy số $b^{1},b^{1,4},b^{1,41},b^{1,414},...$ Những thông tin chi tiết và các công thức có liên quan đều có trong bài viết về lũy thừa.

Định nghĩa

Logarit cơ số $b$ của một số thực dương $x$ là số mũ mà $b$ cần phải được nâng lên để có được $x$ . Nói cách khác, logarit cơ số $b$ của $x$ là nghiệm $y$ của phương trình^[5]

b^{y}=x

và được ký hiệu là $log b x$ .

Trong phương trình $y = log b x$ , giá trị $y$ là câu trả lời cho câu hỏi " $b$ cần được nâng lên số mũ nào để có được $x$ ?".

Ví dụ

$log 2 16 = 4$ vì $24 = 2 \times2 \times 2 \times 2 = 16$ .
Logarit có thể là số âm: $\quad \log _{2}\!{\frac {1}{2}}=-1\quad$ vì $\quad 2^{-1}={\frac {1}{2^{1}}}={\frac {1}{2}}.$
$log 10150$ gần bằng 2,176, một số nằm giữa 2 và 3 vì 150 nằm giữa $102 = 100$ và $103 = 1000.$
Với mọi cơ số $b$ , $log b b = 1$ và $log b 1 = 0$ vì $b 1 = b$ và $b 0 = 1$ .

Các đẳng thức logarit

Các công thức quan trọng sau đây liên hệ các logarit với nhau.^[6]

Tích, thương, lũy thừa và căn

Logarit của một tích là tổng các logarit của các thừa số; logarit của một thương gồm hai số là hiệu logarit của hai số đó. Logarit của một số lũy thừa $p$ bằng $p$ lần logarit của số đó; logarit của căn bậc $p$ là logarit của số đó chia cho $p$ . Bảng dưới đây liệt kê các phép tính logarit cơ bản nêu trên và các ví dụ.^[1] Các đẳng thức đều có được sau khi thay $x=b^{\log _{b}x}$ hoặc $y=b^{\log _{b}y}$ ở vế trái của các biểu thức.

	Công thức	Ví dụ
Tích	$\log _{b}(xy)=\log _{b}x+\log _{b}y$	$\log _{3}243=\log _{3}(9\cdot 27)=\log _{3}9+\log _{3}27=2+3=5$
Thương	$\log _{b}\!{\frac {x}{y}}=\log _{b}x-\log _{b}y$	$\log _{2}16=\log _{2}\!{\frac {64}{4}}=\log _{2}64-\log _{2}4=6-2=4$
Lũy thừa	$\log _{b}\left(x^{p}\right)=p\log _{b}x$	$\log _{2}64=\log _{2}\left(2^{6}\right)=6\log _{2}2=6$
Căn	$\log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}x}{p}}$	$\log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5$

Đổi cơ số

Logarit $log b x$ có thể được tính từ logarit cơ số trung gian $k$ của $x$ và $b$ theo công thức:

\log _{b}x={\frac {\log _{k}x}{\log _{k}b}}.\,

Giải thích phép tính logarit qua cơ số trung gian

Ta đã biết

x=b^{\log _{b}x}

.

Lấy logarit $log k$ cho cả hai vế của biểu thức, ta được

\log _{k}x=\log _{k}\left(b^{\log _{b}x}\right)=\log _{b}x\cdot \log _{k}b

.

Chia cả hai vế cho $\log _{k}b$ , ta được:

\log _{b}x={\frac {\log _{k}x}{\log _{k}b}}

,

cho thấy hệ số quy đổi từ một giá trị $\log _{k}$ đã biết đến giá trị $\log _{b}$ tương ứng là $(\log _{k}b)^{-1}.$

Các máy tính bỏ túi điển hình thường tính logarit cơ số 10 và $e$ .^[7] Logarit cơ số $b$ bất kỳ có thể được xác định bằng cách đưa một trong hai logarit đặc biệt này vào công thức trên:

\log _{b}x={\frac {\log _{10}x}{\log _{10}b}}={\frac {\log _{e}x}{\log _{e}b}}.\,

Cho một số $x$ là logarit cơ số $b$ của nó $log b x$ với $b$ chưa biết, thì $b$ được tính bằng:

b=x^{\frac {1}{\log _{b}x}},

bằng cách mũ hóa biểu thức $x=b^{\log _{b}x}$ lên số mũ $\;{\tfrac {1}{\log _{b}x}}.$

Các cơ số thông dụng

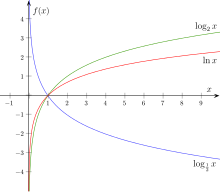
Đồ thị của các hàm logarit cơ số 0,5, 2 và $e$

Trong số các cơ số, có ba cơ số đặc biệt. Chúng gồm $b = 10$ , $b = e$ (hằng số vô tỉ xấp xỉ bằng 2,71828) và $b = 2$ (logarit nhị phân). Trong giải tích toán học, logarit cơ số $e$ là phổ biến nhất nhờ các tính chất được giải thích dưới đây. Mặt khác, có thể dễ dàng tính logarit cơ số 10 trong hệ thập phân:^[8]

\log _{10}(10x)=\log _{10}10+\log _{10}x=1+\log _{10}x.\

Do đó, $log 10 x$ có liên hệ với số chữ số của một số nguyên dương $x$ , đó là số nguyên nhỏ nhất lớn hơn $log 10 x$ .^[9] Chẳng hạn, $log 101430$ gần bằng 3,15. Số nguyên liền sau là 4 và là số chữ số trong số 1430. Logarit tự nhiên và logarit nhị phân thường được dùng trong lý thuyết thông tin, có liên quan đến hai đơn vị cơ bản nhất trong thông tin là nat và bit.^[10] Logarit nhị phân cũng được sử dụng trong khoa học máy tính (hệ nhị phân); trong lý thuyết âm nhạc (quãng tám) và trong nhiếp ảnh để đo giá trị phơi sáng.^[11]

Bảng dưới đây liệt kê các ký hiệu logarit thông dụng và lĩnh vực mà chúng được sử dụng. Một số nơi viết $log x$ thay vì $log b x$ , thậm chí ký hiệu $b log x$ cũng tồn tại.^[12] Cột "Ký hiệu ISO" liệt kê các ký hiệu do Tổ chức tiêu chuẩn hóa quốc tế khuyến nghị (ISO 31-11).^[13] Ký hiệu $log x$ được dùng chung cho cả ba cơ số tùy theo lĩnh vực: trong khoa học máy tính, $log$ thường có nghĩa là $log 2$ ; trong toán học, $log$ thường có nghĩa là $log e$ .^[14]^[1] Trong các trường hợp còn lại, $log$ có nghĩa là $log 10$ .^[15]

Cơ số $b$	Tên gọi của log_bx	Ký hiệu ISO	Các ký hiệu khác	Sử dụng trong
2	logarit nhị phân	$lb x$ ^[16]	$ld x$ , $log x$ , $lg x$ ,^[17] $log 2 x$	khoa học máy tính, lý thuyết thông tin, lý thuyết âm nhạc, nhiếp ảnh
$e$	logarit tự nhiên	$ln x$	$log x$ (trong toán học^[1]^[18] và nhiều ngôn ngữ lập trình)	toán học, vật lý, hóa học, thống kê, kinh tế học, lý thuyết thông tin và kỹ thuật
10	logarit thập phân	$lg x$	$log x$ , $log 10 x$ (trong kỹ thuật, sinh học, thiên văn học)	nhiều lĩnh vực trong kỹ thuật (xem decibel và xem dưới đây), bảng logarit, máy tính bỏ túi, phổ học

Lịch sử

Lịch sử logarit bắt đầu vào thế kỷ 17 tại châu Âu, khi một hàm mới được phát hiện ra đã làm mở rộng lĩnh vực giải tích vượt ra khỏi phạm vi tính toán đại số thông thường. Thuật ngữ logarit xuất hiện lần đầu tiên khi John Napier công bố cuốn sách Mirifici Logarithmorum Canonis Descriptio vào năm 1614.^[19]^[2] Trước Napier, đã có nhiều kỹ thuật khác với phạm vi tương tự, như prosthaphaeresis hay dùng bảng số (do Jost Bürgi phát triển khoảng năm 1600).^[20]^[21]

Logarit thập phân của một số là số mũ khi đưa số đó về dạng lũy thừa của 10.^[22] Những logarit thực đầu tiên là các phương pháp cảm tính để chuyển phép nhân thành phép cộng, tạo điều kiện để tính toán nhanh chóng. Một vài trong số đó có áp dụng bảng số được suy ra từ các đẳng thức lượng giác.^[23]

Quá trình tìm ra một hàm số, sau này được gọi là logarit tự nhiên, bắt đầu khi Grégoire de Saint-Vincent, một tu sĩ dòng Tên người Bỉ sống tại Prague, cố gắng xác định phép cầu phương của một hyperbol vuông. Archimedes đã viết cuốn The Quadrature of the Parabola vào thế kỷ 3 trước Công nguyên, nhưng người ta vẫn chưa biết được cầu phương của hyperbol đến khi Saint-Vincent công bố kết quả vào năm 1647. Sự liên quan của logarit giữa cấp số nhân và cấp số cộng đã thúc đẩy A. A. de Sarasa liên kết cầu phương của Saint-Vincent và logarit trong prosthaphaeresis, dẫn đến thuật ngữ "logarit hyperbol", một thuật ngữ đồng nghĩa với logarit tự nhiên. Về sau, hàm số mới này được Christiaan Huygens và James Gregory đánh giá cao. Ký hiệu Log y do Leibniz tìm ra vào năm 1675 và một năm sau, ông liên hệ nó với tích phân $\int {\frac {dy}{y}}.$ ^[24]

Bảng logarit, thước loga và ứng dụng lịch sử

Bằng cách đơn giản hóa các phép tính phức tạp trước khi máy tính ra đời, logarit đóng góp đáng kể cho sự phát triển của khoa học, đặc biệt là thiên văn học. Nó cũng đóng góp cho sự tiến bộ của khảo sát xây dựng, hàng hải thiên văn và nhiều lĩnh vực khác. Pierre-Simon Laplace đã gọi logarit là

"...[một] thủ thuật đáng ngưỡng mộ mà, bằng cách rút ngắn một công việc vài tháng xuống vài ngày, nhân đôi cuộc đời của một nhà thiên văn, và loại bỏ những sai sót ghê tởm không thể tách rời từ những phép tính dài."^[25]

Vì hàm $f (x) = b x$ là hàm nghịch đảo của $log b x$ nên nó còn được gọi là antilogarit.^[26]

Bảng log

Một công cụ góp phần lớn trong việc ứng dụng logarit vào thực tế là bảng logarit.^[27] Bảng đầu tiên như vậy do Henry Briggs biên soạn năm 1617 ngay sau phát minh của Napier, sử dụng cơ số 10. Bảng đầu tiên của Briggs chứa logarit thập phân của tất cả các số nguyên từ 1 đến 1000, với độ chính xác đến 14 chữ số, tiếp đó là các bảng số trong phạm vi lớn hơn. Các bảng số này liệt kê các giá trị của $log 10 x$ với mỗi số $x$ nằm trong một giới hạn nhất định. Logarit cơ số 10 được sử dụng nhiều nhất trong tính toán, dẫn đến thuật ngữ logarit thập phân, vì logarit của các số sai khác nhau 10 lần khác nhau bởi các số nguyên. Logarit thập phân của $x$ có thể được chia thành phần nguyên và phần thập phân. Bảng logarit chỉ chứa phần thập phân, vì dễ dàng xác định được phần nguyên bằng cách đếm số chữ số từ dấu thập phân.^[28] Phần nguyên của $10 \cdot x$ là 1 cộng cho phần nguyên của $x$ , còn phần thập phân là giống nhau. Bằng cách sử dụng bảng logarit ba chữ số, logarit của 3542 được ước lượng bởi

\log _{10}3542=\log _{10}(1000\cdot 3,542)=3+\log _{10}3,542\approx 3+\log _{10}3,54\,

Nếu dùng nội suy thì độ chính xác cao hơn nhiều:

\log _{10}3542\approx 3+\log _{10}3,54+0.2(\log _{10}3,55-\log _{10}3,54)\

Giá trị của $10 x$ có thể được xác định bằng cách tra cứu ngược lại từ bảng số trên, vì logarit là một hàm số đơn điệu.

Tính toán

Tích và thương của hai số dương $c$ và $d$ thường được tính bằng tổng và hiệu các logarit của chúng. Tích $cd$ hoặc thương $c/d$ có được bằng cách tra cứu antilogarit của tổng và tích đó trong cùng bảng số:

cd=10^{\ \log _{10}c}\,10^{\ \log _{10}d}=10^{\ \log _{10}c+\ \log _{10}d}\,

và

{\frac {c}{d}}=cd^{-1}=10^{\ \log _{10}c-\ \log _{10}d}.\,

Đối với các phép tính toán thông thường, nếu yêu cầu độ chính xác cao, việc tra cứu hai logarit, tính tổng hoặc hiệu của chúng rồi tra cứu antilogarit nhanh hơn rất nhiều so với khi nhân bằng các công cụ trước đây như prosthaphaeresis (vốn phụ thuộc vào đẳng thức lượng giác).

Phép tính lũy thừa và căn được đưa về phép nhân hoặc chia và tra cứu bởi

c^{d}=\left(10^{\ \log _{10}c}\right)^{d}=10^{d\ \log _{10}c}\,

và

{\sqrt[{d}]{c}}=c^{\frac {1}{d}}=10^{{\frac {1}{d}}\ \log _{10}c}.\,

Các bảng số chứa logarit thập phân của các hàm lượng giác tạo điều kiện thuận lợi cho việc tính toán lượng giác.

Thước loga

Một ứng dụng quan trọng khác của logarit là thước loga, một cặp thước chia độ theo logarit được sử dụng trong tính toán. Tiền thân của nó, thước Gunter, được phát minh ngay sau công bố của Napier. William Oughtred sau đó đã phát triển nó lên thành thước loga, một cặp thước logarit có thể trượt lẫn nhau. Các số được đặt trên thước với khoảng cách về độ dài tỉ lệ thuận với hiệu các logarit của chúng. Khi trượt thước bên trên tức là ta đã cộng cơ học các logarit với nhau như hình minh họa:

Ví dụ, cộng khoảng cách từ 1 đến 2 ở thước bên dưới với khoảng cách từ 1 đến 3 ở thước bên trên cho tích của chúng bằng 6. Thước loga từng là một công cụ tính toán thiết yếu của các nhà khoa học cho đến những năm 1970, vì nó cho phép tính toán nhanh hơn nhiều so với kỹ thuật tra bảng số.^[29]

Xem thêm

Tham khảo

^ ^a ^b ^c ^d “The Ultimate Guide to Logarithm — Theory & Applications”. Math Vault. 8 tháng 5 năm 2016.
^ ^a ^b Hobson, Ernest William (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press
^ Remmert, Reinhold. (1991). Theory of complex functions. New York: Springer-Verlag. ISBN 0387971955. OCLC 21118309.
^ Shirali, Shailesh (2002), A Primer on Logarithms, Hyderabad: Universities Press, ISBN 978-81-7371-414-6, đặc biệt chương 2
^ Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8, chương 1
^ Mọi thông tin có thể được tìm thấy trong Shailesh Shirali 2002, chương 4, (Douglas Downing 2003, trang 275) hoặc Kate & Bhapkar 2009, trang 1-1,...
^ Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-005023-5, trang 21
^ Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, NY: Barron's, ISBN 978-0-7641-1972-9, chương 17, trang 275
^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0, trang 20
^ Van der Lubbe, Jan C. A. (1997), Information Theory, Cambridge University Press, tr. 3, ISBN 978-0-521-46760-5
^ Allen, Elizabeth; Triantaphillidou, Sophie (2011), The Manual of Photography, Taylor & Francis, tr. 228, ISBN 978-0-240-52037-7
^ Franz Embacher; Petra Oberhuemer, Mathematisches Lexikon (bằng tiếng Đức), mathe online: für Schule, Fachhochschule, Universität unde Selbststudium, truy cập ngày 17 tháng 6 năm 2020Quản lý CS1: ngôn ngữ không rõ (liên kết)
^ Taylor, B.N. (1995), Guide for the Use of the International System of Units (SI), Bộ Thương mại Hoa Kỳ, Bản gốc lưu trữ ngày 29 tháng 6 năm 2007, truy cập ngày 17 tháng 6 năm 2020
^ Goodrich, Michael T.; Tamassia, Roberto (2002), Algorithm Design: Foundations, Analysis, and Internet Examples, John Wiley & Sons, tr. 23, One of the interesting and sometimes even surprising aspects of the analysis of data structures and algorithms is the ubiquitous presence of logarithms ... As is the custom in the computing literature, we omit writing the base $b$ of the logarithm when $b = 2$ .
^ Parkhurst, David F. (2007). Introduction to Applied Mathematics for Environmental Science . Springer Science & Business Media. tr. 288. ISBN 978-0-387-34228-3.
^ Gullberg, Jan (1997), Mathematics: from the birth of numbers., New York: W. W. Norton & Co, ISBN 978-0-393-04002-9
^ Xem chú thích 1 trong Perl, Yehoshua; Reingold, Edward M. (tháng 12 năm 1977). “Understanding the complexity of interpolation search”. Information Processing Letters. 6 (6): 219–22. doi:10.1016/0020-0190(77)90072-2.
^ Xem Theorem 3.29 trong Rudin, Walter (1984). Principles of mathematical analysis (ấn bản 3). Auckland: McGraw-Hill International. ISBN 978-0-07-085613-4.
^ Napier, John (1614), Mirifici Logarithmorum Canonis Descriptio (bằng tiếng Latin), Edinburgh, Scotland: Andrew HartQuản lý CS1: ngôn ngữ không rõ (liên kết)
^ Folkerts, Menso; Launert, Dieter; Thom, Andreas (tháng 10 năm 2015), Jost Bürgi's Method for Calculating Sines, arXiv:1510.03180, Bibcode:2015arXiv151003180F
^ “Burgi biography”. www-history.mcs.st-and.ac.uk. Truy cập ngày 17 tháng 6 năm 2020.
^ William Gardner (1742) Tables of Logarithms
^ Enrique Gonzales-Velasco (2011) Journey through Mathematics – Creative Episodes in its History, §2.4 Hyperbolic logarithms, trang 117, Springer ISBN 978-0-387-92153-2
^ Florian Cajori (1913) "History of the exponential and logarithm concepts", American Mathematical Monthly 20: 5, 35, 75, 107, 148, 173, 205.
^ Bryant, Walter W. (1907), A History of Astronomy, London: Methuen & Co, p. 44
^ Abramowitz, Milton; Stegun, Irene A. biên tập (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (ấn bản 10), New York: Dover Publications, ISBN 978-0-486-61272-0, chương 4.7., trang 89
^ Campbell-Kelly, Martin (2003), The history of mathematical tables: from Sumer to spreadsheets, Oxford scholarship online, Oxford University Press, ISBN 978-0-19-850841-0, chương 2
^ Spiegel, Murray R.; Moyer, R.E. (2006), Schaum's outline of college algebra, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-145227-4, trang 264
^ Maor 2009, chương 1, 13

Liên kết ngoài

Colin Byfleet, Educational video on logarithms, truy cập 9 tháng 4 năm 2011
Edward Wright, Translation of Napier's work on logarithms, truy cập 9 tháng 4 năm 2011

Bản mẫu:Hệ vi thừa

[:0-1] “The Ultimate Guide to Logarithm — Theory & Applications”. Math Vault. 8 tháng 5 năm 2016.

[:1-2] Hobson, Ernest William (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press

[3] Remmert, Reinhold. (1991). Theory of complex functions. New York: Springer-Verlag. ISBN 0387971955. OCLC 21118309.

[4] Shirali, Shailesh (2002), A Primer on Logarithms, Hyderabad: Universities Press, ISBN 978-81-7371-414-6, đặc biệt chương 2

[5] Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8, chương 1

[6] Mọi thông tin có thể được tìm thấy trong Shailesh Shirali 2002, chương 4, (Douglas Downing 2003, trang 275) hoặc Kate & Bhapkar 2009, trang 1-1,...

[7] Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-005023-5, trang 21

[8] Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, NY: Barron's, ISBN 978-0-7641-1972-9, chương 17, trang 275

[9] Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0, trang 20

[10] Van der Lubbe, Jan C. A. (1997), Information Theory, Cambridge University Press, tr. 3, ISBN 978-0-521-46760-5

[11] Allen, Elizabeth; Triantaphillidou, Sophie (2011), The Manual of Photography, Taylor & Francis, tr. 228, ISBN 978-0-240-52037-7

[12] Franz Embacher; Petra Oberhuemer, Mathematisches Lexikon (bằng tiếng Đức), mathe online: für Schule, Fachhochschule, Universität unde Selbststudium, truy cập ngày 17 tháng 6 năm 2020Quản lý CS1: ngôn ngữ không rõ (liên kết)

[13] Taylor, B.N. (1995), Guide for the Use of the International System of Units (SI), Bộ Thương mại Hoa Kỳ, Bản gốc lưu trữ ngày 29 tháng 6 năm 2007, truy cập ngày 17 tháng 6 năm 2020

[14] Goodrich, Michael T.; Tamassia, Roberto (2002), Algorithm Design: Foundations, Analysis, and Internet Examples, John Wiley & Sons, tr. 23, One of the interesting and sometimes even surprising aspects of the analysis of data structures and algorithms is the ubiquitous presence of logarithms ... As is the custom in the computing literature, we omit writing the base $b$ of the logarithm when $b = 2$ .

[15] Parkhurst, David F. (2007). Introduction to Applied Mathematics for Environmental Science . Springer Science & Business Media. tr. 288. ISBN 978-0-387-34228-3.

[gullberg-16] Gullberg, Jan (1997), Mathematics: from the birth of numbers., New York: W. W. Norton & Co, ISBN 978-0-393-04002-9

[17] Xem chú thích 1 trong Perl, Yehoshua; Reingold, Edward M. (tháng 12 năm 1977). “Understanding the complexity of interpolation search”. Information Processing Letters. 6 (6): 219–22. doi:10.1016/0020-0190(77)90072-2.

[18] Xem Theorem 3.29 trong Rudin, Walter (1984). Principles of mathematical analysis (ấn bản 3). Auckland: McGraw-Hill International. ISBN 978-0-07-085613-4.

[19] Napier, John (1614), Mirifici Logarithmorum Canonis Descriptio (bằng tiếng Latin), Edinburgh, Scotland: Andrew HartQuản lý CS1: ngôn ngữ không rõ (liên kết)

[folkerts-20] Folkerts, Menso; Launert, Dieter; Thom, Andreas (tháng 10 năm 2015), Jost Bürgi's Method for Calculating Sines, arXiv:1510.03180, Bibcode:2015arXiv151003180F

[21] “Burgi biography”. www-history.mcs.st-and.ac.uk. Truy cập ngày 17 tháng 6 năm 2020.

[22] William Gardner (1742) Tables of Logarithms

[23] Enrique Gonzales-Velasco (2011) Journey through Mathematics – Creative Episodes in its History, §2.4 Hyperbolic logarithms, trang 117, Springer ISBN 978-0-387-92153-2

[24] Florian Cajori (1913) "History of the exponential and logarithm concepts", American Mathematical Monthly 20: 5, 35, 75, 107, 148, 173, 205.

[25] Bryant, Walter W. (1907), A History of Astronomy, London: Methuen & Co, p. 44

[26] Abramowitz, Milton; Stegun, Irene A. biên tập (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (ấn bản 10), New York: Dover Publications, ISBN 978-0-486-61272-0, chương 4.7., trang 89

[27] Campbell-Kelly, Martin (2003), The history of mathematical tables: from Sumer to spreadsheets, Oxford scholarship online, Oxford University Press, ISBN 978-0-19-850841-0, chương 2

[28] Spiegel, Murray R.; Moyer, R.E. (2006), Schaum's outline of college algebra, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-145227-4, trang 264

[ReferenceA-29] Maor 2009, chương 1, 13

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]