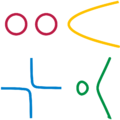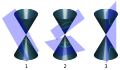Đa tạp
Bài viết này cần thêm chú thích nguồn gốc để kiểm chứng thông tin. |

Một đa tạp tô pô chiều là một không gian tô pô mà mỗi điểm có lân cận đồng phôi với tập con mở của , nói một cách khác, là không gian tôpô tách được với mỗi điểm của nó có một lân cận đồng phôi với một tập mở trong không gian Euclide chiều. Đa tạp chính là khái niệm toán học mở rộng của đường và mặt.
-
Bốn bản đồ trên đường tròn.
-
Một bản đồ trên đường tròn chỉ thiếu một điểm.
-
Các đường cong đại số.
-
Bản đồ tạo bởi phép chiếu nửa trên mặt cầu lên cái đĩa.
-
Một hình trụ hữu hạn là một đa tạp với biên.
-
Chai Klein dìm trong không gian ba chiều.
Định nghĩa[sửa | sửa mã nguồn]
A đa tạp là một không gian tô pô thỏa mãn:[1]
- là Hausdorff và có một cơ sở đếm được (i.e. khả ly).
- đồng phôi địa phương với các tập mở của với cố định, tức là với mọi , tồn tại một lân cận mở chứa và một đồng phôi với . Một cặp như vậy được gọi là một bản đồ (hay một hệ tọa độ). Một tập hợp các bản đồ phủ được gọi là một át-lát của .
- Các ánh xạ chuyển bản đồ (hay đổi hệ tọa độ) là các hàm trơn.
- (Tập hợp tất cả các bản đồ tương thích với cấu trúc vi phân của được gọi là át-lát tối đại của ).
Ta cũng có thể thay điều kiện các hàm trơn bằng các hàm khả vi lần. Khi đó đa tạp được gọi là trơn bậc .
Ví dụ theo số chiều[sửa | sửa mã nguồn]
Đường: Đa tạp một chiều[sửa | sửa mã nguồn]
Một đa tạp tô pô 1 chiều là một không gian topo mà mỗi điểm của nó có một lân cận đồng phôi với không gian Euclid
Một đa tạp 1 chiều liên thông được gọi là 1 đường.
Nếu liên tục thì đồ thị của là một đa tạp 1 chiều. (Nói chung, cho là một hàm liên tục, với n là một tập mở. Khi đó, đồ thị của , tập là một không gian con của n+1, là một đa tạp chiều.)
Đường thẳng thực , đường tròn , đường thẳng xạ ảnh đều là các đa tạp một chiều.
-
Đường parabol
-
Hình vẽ cổ đại về các đường.
-
Các mặt cắt của hình nón là các đường cong được nghiên cứu ở Hy Lạp cổ: đường pa-ra-bôn, đường e-líp và đường hy-pê-bôn.
-
■ hai đường tròn, ■ một đường pa-ra-bôn, ■ một đường hy-pê-bôn, ■ một đường bậc ba
Mặt: đa tạp hai chiều[sửa | sửa mã nguồn]
Một đa tạp tô pô 2 chiều là một không gian topo Hausdorff mà mỗi điểm của nó có một lân cận đồng phôi với không gian Euclid 2
Một đa tạp 2 chiều liên thông được gọi là một mặt
Mặt phẳng là một mặt. Nó liên thông và Hausdorff. Cho điểm , quả cầu mở tâm , bán kính bằng 1 là một lân cận của và đồng phôi với hình đĩa mở. Hơn nữa, mặt phẳng có một cơ sở đếm được được cho bởi tập những quả cầu mở, bán kính hữu tỉ, tâm tại điểm với hữu tỉ.
Mọi tập con mở liên thông của mặt phẳng cũng là một mặt.
Hình xuyến là một đa tạp 2 chiều
-
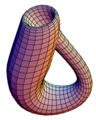
Hình xuyến thắt nút trong không gian ba chiều.
-
Hình xuyến
-
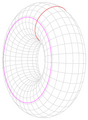
Vòng tròn màu đỏ được quét xung quanh trục định bởi vòng tròn màu hồng.
Dải Mobius là một đa tạp hai chiều.
-
Dải Mobius
Mặt cầu , mặt phẳng xạ ảnh thức , chai Klein, hình trụ , chai Klein bậc bốn (Klein quartic) đều là các đa tạp hai chiều.
Một mặt chứa một dải Mobius nhúng thì được gọi là một mặt không định hướng. Ngược lại thì là một mặt có định hướng.
3-đa tạp: Đa tạp ba chiều[sửa | sửa mã nguồn]
Một đa tạp 3 chiều là không gian topo trong đó mỗi điểm có lân cận đồng phôi với không gian Euclid 3 chiều .
Phần trong của khối lập phương, mặt cầu ba chiều , nhóm Lie - không gian xạ ảnh , mặt xuyến , các quả cầu đồng điều Poincaré (Poincaré homology spheres), đa tạp Whitehead, đạ tạp Weeks, Khối xuyến, Chai Klein rắn (Solid Klein bottle) đều là các đa tạp 3 chiều.
Một đa tạp 3 chiều là không định hướng nếu nó chứa 1 chai Klein (i.e. tồn tại một phép nhúng từ chai Klein tới đa tạp đó). Nếu không thì khi đó đa tạp 3 chiều được gọi là có định hướng.
4-đa tạp: Đa tạp 4 chiều[sửa | sửa mã nguồn]
Hình cầu ngoại lai (exotic), , đa tạp .
Đa tạp nhiều chiều hơn[sửa | sửa mã nguồn]
- Mặt cầu là đa tạp chiều. Sử dụng phép chiếu nổi ta chỉ ra rằng phủ với 2 lân cận và đồng phôi với .
- Mọi tập con mở của là đa tạp chiều.
- Một đa tạp chiều cũng được gọi là một -đa tạp.
Đa tạp vô hạn chiều[sửa | sửa mã nguồn]
Đa tạp Hilbert, đa tạp Banach, đa tạp Fréchet, đa tạp các phép đồng phôi trên một đa tạp vi phân.
Đa tạp con[sửa | sửa mã nguồn]
Đa tạp con là một tập hợp con của một đa tạp mà chính nó là một đa tạp, nhưng có số chiều nhỏ hơn. Đường xích đạo của một hình cầu là một đa tạp con. Nhiều ví dụ phổ biến của đa tạp là đa tạp con của không gian Euclid.
Một đa tạp con cũng là một phép nhúng .
Các đối tượng nghiên cứu[sửa | sửa mã nguồn]
Mỗi lớp các đối tượng nghiên cứu sau đây lập thành một phạm trù. Ta có phạm trù các đa tạp đại số, các đa tạp với biên, các đa tạp với góc cạnh, vân vân.
Đa tạp đại số[sửa | sửa mã nguồn]
Xét tập hợp tất cả các điểm trong không gian phức chiều thỏa mãn hệ phương trình dạng trong đó là các đa thức của các biến số .
- Nếu các đều là bậc nhất đối với tất cả các thì ta có đa tạp tuyến tính
- Nếu các hệ số của là số hữu tỉ (thực, phức) thì ta có Đa tạp đại số hữu tỉ (thực, phức).
Đa tạp với biên (manifold with boundary)[sửa | sửa mã nguồn]
Một tờ giấy dài vô hạn nhưng rộng hữu hạn là một đa tạp 2 chiều với biên 1 chiều. Biên của một đa tạp n chiều với biên là một đa tạp (n-1) chiều. Một đĩa (vòng tròn cộng với phần trong) là đa tạp 2 chiều với biên. Biên của nó là một vòng tròn, một đa tạp 1 chiều. Một quả bóng (hình cầu cộng với phần trong) là một đa tạp 3 chiều với biên. Biên của nó là một mặt cầu, đa tạp 2 chiều.
Đa tạp với biên là một không gian có chứa cả điểm trong và các điểm biên. Tất cả các điểm trong có một lân cận đồng phôi với quả cầu -chiều mở . Tất cả các điểm biên có một lân cận đồng phôi với "một nửa" quả cầu -chiều . Các đồng phôi phải biến mỗi điểm biên thành một điểm có .
Đa tạp với góc cạnh (manifold with corners)[sửa | sửa mã nguồn]
Đa tạp với góc cạnh khác đa tạp với biên ở điều kiện đồng phôi địa phương. Tất cả các điểm trong vẫn có một lân cận đồng phôi với quả cầu -chiều mở . Tuy nhiên, tất cả các điểm biên có một lân cận đồng phôi với "một góc" bậc của quả cầu -chiều . Một góc bậc là một điểm trong. Một góc bậc là một điểm tại biên. Một góc bậc không phải là một điểm trong hay một điểm tại biên Một hình vuông hay một tờ giấy hữu hạn tính cả phần trong cũng là một đa tạp 2 chiều với góc cạnh.[2]
Đa tạp phức[sửa | sửa mã nguồn]
Đa tạp Riemann[sửa | sửa mã nguồn]
Đa tạp symplectic.[sửa | sửa mã nguồn]
Một số định lý liên quan đến đa tạp[sửa | sửa mã nguồn]
Định lý nhúng Whitney[sửa | sửa mã nguồn]
Trong toán học, đặc biệt trong Topo vi phân, có hai định lý nhúng Whitney, được đặt theo tên nhà toán học người Mỹ, Hassler Whitney (1907 – 1989).
- Định lý nhúng Whitney mạnh phát biểu rằng bất kì đa tạp chiều thực trơn (cũng phải là Hausdorff và second-countable) có thể nhúng trơn trong không gian thực , nếu . Đây là giới hạn tuyến tính nhất trong không gian Euclidean có chiều nhỏ nhất, mà tất cả đa tạp chiều được nhúng trong đó. Vì những không gian xạ ảnh thực của chiều không thể được nhúng vào không gian thực nếu là lũy thừa của 2 (có thể thấy từ lý luận lớp đặc trưng (characteristic class argument) của Whitney).
- Định lý nhúng Whitney yếu phát biểu rằng bất kỳ hàm liên tục từ đa tạp chiều đến đa tạp chiều có thể được dự đoán bởi một phép nhúng miễn là . Whitney chứng minh tương tự rằng một ánh xạ có thể được dự đoán bởi một phép dìm miễn là . Kết quả cuối cùng này cũng được gọi là định lý dìm Whitney.
Định lý đa tạp ổn định[sửa | sửa mã nguồn]
Đặt:
là 1 ánh xạ trơn với điểm hypebon cố định tại . Chúng ta ký hiệu tập hợp ổn định và tập hợp không ổn định của . Định lý [1][2][3] phát biểu rằng:
- là một đa tạp trơn và không gian tiếp xúc của nó có cùng số chiều như không gian ổn định của khi tuyến tính hóa tại .
- là một đa tạp trơn và không gian tiếp xúc của nó có cùng số chiều như không gian không ổn định khi tuyến tính hóa tại .
Theo đó, là một đa tạp ổn định và là một đa tạp không ổn định.
Định lý Birkhoff[sửa | sửa mã nguồn]
- Nhà toán học người Mỹ, Garrett Birkhoff (1911 – 1996) đã chứng minh tương tự hai định nghĩa của đa tạp ở trên, một kết quả có ý nghĩa cơ bản với đại số phổ quát và được biết đến như định lý Birkhoff hoặc là định lý HSP. H, S, và P viết tắt cho những phép tính đóng của phép đồng hình, đại số con và tích số.
- Một lớp phương trình (equational class) ký hiệu Σ nào đó, là tập hợp của tất cả mô hình, theo ý nghĩa của lý thuyết mô hình, nó đã thỏa tập hợp phương trình E nào đó, (asserting equality between terms). Một mô hình thỏa những phương trình đó nếu chúng đúng trong mô hình cho mọi giá trị của biến. Những phương trình trong E sau đó được gọi là những đồng nhất thức của mô hình. Ví dụ của những đồng nhất thức đó là luật giao hoán, đại số giao hoán đặc trưng, và luật hút thu, dàn (lattices) đặc trưng.
- Dễ dàng thấy rằng lớp đại số thỏa tập hợp phương trình nào đó sẽ đóng trong phép toán HSP. Chứng minh ngược lại – các lớp đại số đóng trong phép toán HSP phải thuộc phương trình – sẽ khó hơn nhiều.
Xem thêm[sửa | sửa mã nguồn]
Tham khảo[sửa | sửa mã nguồn]
- ^ Đoàn Quỳnh (2000), tr. 292
- ^ Melrose, Richard. “Differential Analysis on manifolds with corners”.
Thư mục[sửa | sửa mã nguồn]
- Colin Adam và Robert Franzosa, Introduction to topology: pure and applied
- Đoàn Quỳnh, 2000, Hình học vi phân, Nhà xuất bản giáo dục
Liên kết ngoài[sửa | sửa mã nguồn]
- Đa tạp và bài toán Poincaré tại Diễn đàn toán học.
| Các chủ đề chính trong toán học |
|---|
| Nền tảng toán học | Đại số | Giải tích | Hình học | Lý thuyết số | Toán học rời rạc | Toán học ứng dụng | Toán học giải trí | Toán học tô pô | Xác suất thống kê |