Giá trị riêng và vectơ riêng

Trong đại số tuyến tính, một vectơ riêng hay vectơ đặc trưng (Tiếng Anh: eigenvector) của một biến đổi tuyến tính là một vectơ khác vectơ không mà được nhân với một hệ số vô hướng khi biến đổi tuyến tính đó được áp dụng lên nó. Hệ số vô hướng tương ứng, thường được ký hiệu là ,[1] được gọi là giá trị riêng (Tiếng Anh: eigenvalue).
Nói một cách hình học, một vectơ riêng tương ứng với một giá trị riêng thực khác 0 có cùng phương sau khi nó được kéo dài ra bởi phép biến đổi và giá trị riêng là hệ số nhân. Nếu giá trị riêng là âm thì vectơ sẽ đổi chiều.[2] Một cách dễ hiểu, trong một không gian vectơ đa chiều, vectơ riêng không bị quay đi.
Định nghĩa chính tắc
[sửa | sửa mã nguồn]Giả thiết T là một biến đổi tuyến tính từ một không gian vectơ V trên trường F vào chính nó và v là một vectơ khác 0 trong V.
Vậy thì v là một vectơ riêng của T khi ảnh của nó qua phép biến đổi T(v) bằng một vô hướng nhân với v. Tức là:
trong đó λ là một vô hướng trong F, gọi là giá trị riêng, giá trị đặc trưng, hay nghiệm đặc trưng tương ứng với v.
Có sự tương ứng trực tiếp giữa các ma trận vuông cấp n và các biến đổi tuyến tính tự đồng cấu từ một không gian vectơ n chiều vào chính nó, trên cơ sở bất kỳ của không gian vectơ. Vì vậy trong một không gian vectơ hữu hạn chiều, việc định nghĩa giá trị riêng và vectơ riêng sử dụng ngôn ngữ của ma trận và ngôn ngữ biến đổi tuyến tính là tương đương.[3][4]
Nếu V là hữu hạn chiều, phương trình trên là tương đương với[5]
trong đó A là ma trận vuông biểu diễn cho tự đồng cấu T và u là vectơ tọa độ của v.
Tổng quan
[sửa | sửa mã nguồn]Vectơ riêng và giá trị riêng có vai trò nổi bật trong việc phân tích các biến đổi tuyến tính. Trong tiếng Anh, giá trị riêng và vectơ riêng tương ứng được gọi là eigenvalue và eigenvector (/ˈaɪɡənˌvɛktər/). Tiền tố eigen- được mượn từ tiếng Đức eigen (cùng gốc với từ tiếng Anh own), nghĩa là "sở hữu", "đặc trưng".[6][7] Ban đầu được sử dụng để nghiên cứu các trục chính của sự quay của các vật rắn, giá trị riêng và vectơ riêng ngày càng có nhiều ứng dụng, ví dụ: trong phân tích ổn định, phân tích rung động, lý thuyết orbital nguyên tử, nghiên cứu băng hà trong địa chất, hệ số lây nhiễm cơ bản, và công nghệ nhận diện khuôn mặt.
Về bản chất, một vectơ riêng v của một biến đổi tuyến tính T là một vectơ khác vectơ không sao cho nó vẫn giữ được hướng ban đầu khi T tác động lên. Tác động của T lên vectơ riêng chỉ làm kéo dài vectơ riêng, được gấp một giá trị vô hướng λ, gọi là giá trị riêng. Điều kiện này có thể được viết dưới dạng phương trình
được gọi là phương trình đặc trưng. Tổng quát, λ có thể là một vô hướng bất kỳ. Chẳng hạn, λ có thể là âm, trong trường hợp này vectơ riêng sẽ đảo chiều khi nó được kéo dài, hoặc giá trị riêng có thể bằng 0 hoặc là số phức.

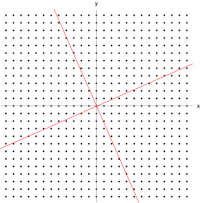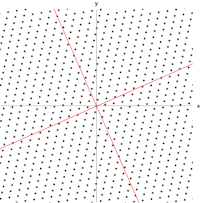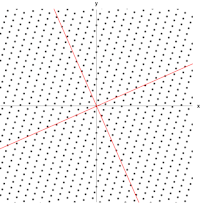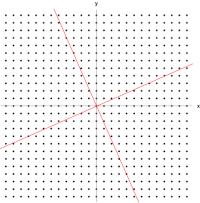
Ví dụ bức vẽ Mona Lisa sau đây là một minh họa đơn giản. Mỗi điểm của hình vẽ có thể được biểu diễn bằng một vectơ từ trung tâm của hình đến điểm đó. Biến đổi tuyến tính trong ví dụ này được gọi là phép ánh xạ trượt. Các điểm ở nửa trên bức vẽ bị dịch sang phải, còn các điểm ở nửa dưới bị dịch sang trái, tỉ lệ thuận với khoảng cách của chúng so với trục hoành ở giữa bức vẽ. Các vectơ tương ứng với mỗi điểm trong bức vẽ ban đầu vì vậy bị trượt sang bên trái hoặc phải, và bị làm cho ngắn vào hoặc dài ra bởi phép biến đổi. Ta cũng có thấy rằng những điểm nằm dọc theo trục hoành không bị di chuyển đi khi phép biến đổi tác động. Vì vậy, mỗi vectơ chỉ trực tiếp sang trái hoặc phải mà không có thành phần thẳng đứng là một vectơ riêng của phép biến đổi này, vì phép biến đổi không ảnh hưởng tới hướng của nó. Hơn nữa, trong ví dụ này các vectơ riêng trên đều có giá trị riêng bằng 1, vì vậy phép biến đổi cũng không làm độ dài của chúng thay đổi.
Các biến đổi tuyến tính có thể có nhiều dạng, chúng ánh xạ các vectơ trong nhiều loại không gian vectơ, vì thế vectơ riêng cũng có thể có nhiều dạng. Ví dụ, biến đổi tuyến tính có thể là một toán tử vi phân như , trong trường hợp này các vectơ riêng là các hàm được gọi là hàm riêng được nhân thêm bởi toán tử vi phân đó, chẳng hạn
Ngoài ra, biến đổi tuyến tính có thể có dạng một ma trận n × n, trong trường hợp này các vectơ là các ma trận cột n × 1. Nếu biến đổi tuyến tính được biểu diễn dưới dạng ma trận A cỡ n × n thì phương trình giá trị riêng ở trên có thể được viết lại dưới dạng phép nhân ma trận
trong đó vectơ riêng v là một ma trận cột n × 1. Đối với ma trận, các vectơ riêng và giá trị riêng có thể được sử dụng vào việc phân rã ma trận—ví dụ bằng cách chéo hóa nó.
Giá trị riêng và vectơ riêng làm phát sinh nhiều khái niệm toán học có liên quan chặt chẽ, và chữ riêng hay tiền tố eigen- dùng để đặt tên chúng:
- Tập hợp các vectơ riêng của một biến đổi tuyến tính, mỗi vectơ được ghép cặp với giá trị riêng tương ứng, được gọi là hệ riêng của biến đổi đó.[8][9]
- Tập hợp tất cả vectơ riêng của biến đổi T tương ứng với cùng một giá trị riêng, cùng với vectơ không, được gọi là một không gian con riêng, hay không gian con đặc trưng tương ứng với giá trị riêng đó của T.[10]
- Nếu một tập hợp các vectơ riêng của T tạo thành một cơ sở của không gian miền xác định của T thì cơ sở này được gọi là một cơ sở riêng của T.
Lịch sử
[sửa | sửa mã nguồn]Trong các giáo trình, giá trị riêng thường được giới thiệu trong ngữ cảnh đại số tuyến tính hay lý thuyết ma trận. Tuy nhiên, về mặt lịch sử, khái niệm này phát sinh từ nghiên cứu các dạng toàn phương và phương trình vi phân.
Vào thế kỷ thứ 18, Leonhard Euler đã nghiên cứu về chuyển động quay của một vật rắn và khám phá ra vai trò của các trục chính.[a] Joseph-Louis Lagrange nhận ra rằng các trục chính là các vectơ riêng của ma trận quán tính.[11]
Vào đầu thế kỷ thứ 19, Augustin-Louis Cauchy đã thấy cách mà các công trình của họ có thể được sử dụng vào việc phân loại các mặt bậc hai, và đã tổng quát hóa nó cho trường hợp số chiều tùy ý.[12] Cauchy cũng là người đặt ra thuật ngữ racine caractéristique (nghiệm đặc trưng) cho cái ngày nay được gọi là eigenvalue (giá trị riêng); thuật ngữ của ông gắn với phương trình đặc trưng.[b]
Sau đó, Joseph Fourier ứng dụng các công trình của Lagrange và Pierre-Simon Laplace vào việc giải phương trình nhiệt bằng phép tách biến số trong cuốn Théorie analytique de la chaleur xuất bản năm 1822.[13] Charles-François Sturm đã phát triển thêm các ý tưởng của Fourier, và đã thu hút được sự quan tâm của Cauchy, người đã kết hợp chúng với các ý tưởng của riêng ông và đã đi đến kết quả rằng các ma trận đối xứng thực có các giá trị riêng thực.[12] Kết quả này được mở rộng hơn bởi Charles Hermite vào năm 1855 đối với cái mà ngày nay gọi là ma trận Hermite.[14]
Khoảng cùng thời gian đó, Francesco Brioschi đã chứng minh được các giá trị riêng của ma trận trực giao nằm trên đường tròn đơn vị,[12] và Alfred Clebsch đã tìm ra kết quả tương ứng cho ma trận đối xứng chéo.[14] Cuối cùng, Karl Weierstrass đã làm rõ một khía cạnh quan trọng trong lý thuyết ổn định khởi xướng bởi Laplace, bằng cách nhận ra rằng các ma trận khiếm khuyết (defective) có thể gây ra sự mất ổn định.[12]
Cũng trong cùng thời gian này, Joseph Liouville đã nghiên cứu các vấn đề về giá trị riêng tương tự các vấn đề của Sturm; phân ngành được phát sinh từ công trình của họ ngày nay được gọi là lý thuyết Sturm–Liouville.[15] Schwarz đã nghiên cứu giá trị riêng đầu tiên của phương trình Laplace trên các miền tổng quát, đến hồi cuối thế kỷ 19, trong khi đó Poincaré nghiên cứu phương trình Poisson sau đó vài năm.[16]
Vào đầu thế kỷ 20, David Hilbert đã nghiên cứu các giá trị riêng của các toán tử tích phân bằng cách coi các toán tử là các ma trận vô hạn.[17] Ông là người đầu tiên sử dụng từ tiếng Đức eigen, có nghĩa là "sở hữu",[7] để chỉ các vectơ riêng và giá trị riêng vào năm 1904,[c] mặc dù ông có thể đã dựa theo một cách dùng từ liên quan bởi Hermann von Helmholtz. Một thời gian thuật ngữ tiêu chuẩn để chỉ giá trị riêng trong tiếng Anh là "proper value", nhưng ngày nay thuật ngữ dễ nhận biết hơn "eigenvalue" là từ tiêu chuẩn.[18]
Thuật toán tính số đầu tiên cho việc tính toán các giá trị riêng và vectơ riêng ra đời vào năm 1929, khi Richard von Mises xuất bản phương pháp lặp lũy thừa. Một trong những phương pháp phổ biến nhất hiện nay, thuật toán QR, được đề xuất một cách độc lập bởi John G. F. Francis[19] và V. Kublanovskaya[20] năm 1961.[21][22]
Giá trị riêng và vectơ riêng của ma trận
[sửa | sửa mã nguồn]Giá trị riêng và vectơ riêng thường được giới thiệu đến sinh viên khi học về các khóa đại số tuyến tính tập trung vào các ma trận.[23][24] Hơn nữa, các biến đổi tuyến tính trên một không gian vectơ hữu hạn chiều có thể được biểu diễn nhờ sử dụng các ma trận,[25][4] điều này đặc biệt phổ biến trong các ứng dụng tính toán số.[26]
Để bắt đầu, ta xét các vectơ n chiều gồm bộ n phần tử có thứ tự, ví dụ các vectơ ba chiều sau
Các vectơ này được gọi là các bội vô hướng của nhau, hay song song hoặc cùng phương, nếu tồn tại một vô hướng λ sao cho
Trong trường hợp này .
Bây giờ xét biến đổi tuyến tính trên các vectơ n chiều được xác định bởi một ma trận A cỡ n × n,
hay
trong đó đối với mỗi hàng ta có,
- .
Nếu v và w là các bội vô hướng của nhau, tức là nếu
-
(1)
thì v là một vectơ riêng của biến đổi tuyến tính A và hệ số nhân λ là giá trị riêng tương ứng với vectơ riêng đó. Phương trình (1) là phương trình giá trị riêng cho ma trận A. Phương trình (1) có thể được nêu một cách tương đương dưới dạng
-
(2)
trong đó I là ma trận đơn vị n × n và 0 là vectơ không.
Giá trị riêng và đa thức đặc trưng
[sửa | sửa mã nguồn]Phương trình (2) có nghiệm vectơ v khác 0 (gọi là nghiệm không tầm thường) khi và chỉ khi định thức của ma trận (A − λI) bằng 0. Vì vậy các giá trị riêng của A là các giá trị λ thỏa mãn phương trình
-
(3)
Sử dụng quy tắc Leibniz cho định thức, vế trái của Phương trình (3) là một hàm số đa thức với biến λ và bậc của đa thức này là n, bằng cấp của ma trận A. Các hệ số của đa thức này phụ thuộc vào các phần tử của ma trận A, ngoại trừ hệ số của bậc n luôn là (−1)nλn. Đa thức này được gọi là đa thức đặc trưng của A. Còn Phương trình (3) được gọi là phương trình đặc trưng của A. Từ định lý cơ bản của đại số ta suy ra rằng đa thức đặc trưng của một ma trận vuông A cấp n là một đa thức có bậc n, và có thể được phân tích thành tích của n nhân tử tuyến tính,
-
(4)
trong đó mỗi λi có thể là số thực hoặc phức. Các số λ1, λ2, ... λn có thể không phân biệt, và là các nghiệm của đa thức và là giá trị riêng của A.
Lấy một ví dụ ngắn (sẽ được mô tả chi tiết ở mục ví dụ bên dưới), xét ma trận
Lấy định thức của ma trận (A − λI), ta có đa thức đặc trưng của A là
Cho đa thức đặc trưng bằng 0 để có phương trình, nó có hai nghiệm tại λ=1 và λ=3, là hai giá trị riêng của A. Các vectơ riêng tương ứng với các giá trị riêng có thể tìm được bằng cách giải ra các thành phần của v trong phương trình bằng cách chuyển về hệ phương trình tuyến tính thuần nhất. Trong ví dụ này, mọi vectơ riêng là bội vô hướng khác 0 bất kỳ của hai vectơ riêng
Nếu các phần tử của ma trận A đều là các số thực thì các hệ số của đa thức đặc trưng cũng là các số thực, nhưng các giá trị riêng có thể vẫn có phần ảo khác 0. Các tọa độ của các vectơ riêng tương ứng cũng có thể có phần ảo khác 0. Tương tự, các giá trị riêng có thể là các số vô tỉ ngay cả khi các phần tử của A đều là các số hữu tỉ, hay thậm chí nếu tất cả chúng đều là số nguyên. Tuy nhiên nếu các phần tử của ma trận A đều là các số đại số (bao gồm cả các số hữu tỉ), các giá trị riêng sẽ là các số phức đại số.
Các nghiệm phức của một đa thức thực với các hệ số thực có thể được nhóm thành cặp các liên hợp phức, tức là hai số của mỗi cặp chỉ có dấu khác nhau ở phần ảo còn phần thực thì giống nhau. Nếu bậc đa thức là lẻ thì theo định lý giá trị trung gian, ít nhất một nghiệm là thực. Vì thế, một ma trận thực vuông với số cấp lẻ có ít nhất một giá trị riêng thực, trong khi một ma trận thực vuông với số kích thước chẵn có thể không có bất kỳ một giá trị riêng thực nào. Các vectơ riêng tương ứng với các giá trị riêng phức này cũng là phức và cũng theo từng cặp liên hợp phức.
Việc tính toán bằng số định thức và đa thức đặc trưng trong thực tế là một vấn đề hoàn toàn khác với các lý thuyết nói ở trên. Tính toán ngày càng khó khăn với các ma trận có kích thước càng lớn, chưa kể các lỗi làm tròn không thể tránh khỏi. Kể từ ma trận cỡ bằng 5 trở lên, đa thức đặc trưng là bậc 5 hoặc cao hơn và do đó theo định lý Abel–Ruffini, không có công thức đại số tường minh cho các nghiệm giá trị riêng cho các ma trận này. Vì thế, người ta đưa ra các phương pháp tính xấp xỉ số để tính toán giá trị riêng và vectơ riêng. Thuật toán tính giá trị riêng bằng số sớm nhất là phép lặp lũy thừa, sau đó các thuật toán chính xác và hiệu quả hơn đã ra đời, chẳng hạn thuật toán QR vào năm 1961.[27] Đối với các ma trận Hermite thưa, thuật toán Lanczos là một ví dụ về một phương pháp lặp hiệu quả để tính giá trị riêng và vectơ riêng, và còn được sử dụng trong nhiều mục đích có thể khác.[27]
Số bội đại số
[sửa | sửa mã nguồn]Cho λi là một giá trị riêng của ma trận A cỡ n × n. Số bội đại số μA(λi) của một giá trị riêng λi là số bội của nghiệm λi của đa thức đặc trưng, tức là số nguyên dương lớn nhất k sao cho đa thức đó chia hết cho (λ − λi)k.[10][28][29]
Giả sử ma trận vuông A có kích thước n và có d ≤ n các giá trị riêng phân biệt. Ở Phương trình (4) đa thức đặc trưng của A được phân tích thành tích của n thừa số tuyến tính với một vài thừa số có thể lặp lại, nhưng thay vào đó ta có thể viết đa thức đặc trưng thành tích của d thừa số, mỗi thừa số chỉ tương ứng với một giá trị riêng riêng biệt và được lũy thừa lên bậc bằng số lần lặp, chính là số bội đại số.
Nếu d = n thì ở vế phải là tích của n thừa số tuyến tính tương tự Phương trình (4). Số bội đại số của mỗi giá trị riêng liên hệ với kích thước của ma trận n như sau.
Nếu μA(λi) = 1, thì λi được gọi là giá trị riêng đơn.[29] Nếu μA(λi) bằng số bội hình học của λi , γA(λi), được định nghĩa ở mục sau, thì λi được gọi là giá trị riêng nửa đơn.
Không gian con riêng, số bội hình học và cơ sở riêng của ma trận
[sửa | sửa mã nguồn]Cho một giá trị riêng cụ thể λ của một ma trận A cỡ n × n. Định nghĩa E là tập hợp tất cả vectơ v thỏa mãn Phương trình (2),
Mặt khác, tập hợp này chính là hạt nhân của ma trận (A − λI). Lại có, theo định nghĩa, bất kỳ một vectơ khác vectơ không nào thỏa mãn điều kiện này là một vectơ riêng của A tương ứng với λ. Vì thế, tập hợp E là hợp của vectơ không với tập hợp tất cả vectơ riêng của A tương ứng với λ, và E bằng tập hợp hạt nhân của (A − λI). E được gọi là không gian con riêng hay không gian con đặc trưng của A tương ứng với giá trị riêng λ.[30][10] Tổng quát, λ là một số phức và các vectơ riêng là các ma trận cột n × 1 phức. Một tính chất của hạt nhân là nó cũng là một không gian con tuyến tính, nên E là một không gian con của ℂn.
Bởi không gian con riêng E là một không gian con tuyến tính, nó là đóng đối với phép cộng. Tức là, nếu hai vectơ u và v thuộc tập E, được viết là u, v ∈ E, thì vectơ tổng (u + v) ∈ E, hay tương đương là A(u + v) = λ(u + v): với cùng λ, tổng của hai vectơ riêng cũng là một vectơ riêng. Có thể kiểm tra điều này bằng cách sử dụng tính phân phối của phép nhân ma trận. Tương tự, vì E là không gian con tuyến tính nên nó đóng đối với phép nhân vô hướng. Tức là, nếu v ∈ E và α là một số phức, ta có (αv) ∈ E hay tương đương là A(αv) = λ(αv): mỗi vectơ song song với một vectơ riêng cũng là một vectơ riêng. Có thể kiểm tra điều này bằng cách chú ý rằng phép nhân vô hướng của các số phức với ma trận phức có tính giao hoán. Vậy tóm lại nếu các vectơ u + v và αv khác vectơ không thì chúng cũng là các vectơ riêng của A tương ứng với λ.
Số chiều của không gian con riêng E ứng với giá trị riêng λ, hay số vectơ riêng độc lập tuyến tính tối đa ứng với λ, được gọi là số bội hình học γA(λ) của giá trị riêng đó. Bởi E còn là hạt nhân của (A − λI), số bội hình học của λ cũng là số chiều của hạt nhân, hay còn gọi là số vô hiệu của ma trận (A − λI), được liên hệ với kích thước và hạng của (A − λI) bởi
Bởi theo định nghĩa của giá trị riêng và vectơ riêng, số bội hình học của một giá trị riêng phải ít nhất bằng 1, tức là ứng với mỗi giá trị riêng có ít nhất một vectơ riêng. Hơn nữa, số bội hình học của một vectơ riêng không thể vượt quá số bội đại số của nó. Ngoài ra, nhớ lại rằng số bội đại số của một giá trị riêng không thể vượt quá n:
Để chứng minh bất đẳng thức , trước tiên thấy rằng từ định nghĩa số bội hình học suy ra được sự tồn tại của các vectơ riêng trực chuẩn sao cho . Vì thế ta có thể tìm được một ma trận (unita) với cột đầu tiên là các vectơ riêng này, và các cột còn lại là một tập hợp trực chuẩn gồm vectơ và chúng trực giao với các vectơ riêng của . Vì vậy có hạng đầy đủ tức là nó khả nghịch, và với là ma trận mà khối ở phía trên bên trái là ma trận đường chéo . Từ đẳng thức này ta có . Nói cách khác, đồng dạng với , suy ra rằng . Nhưng từ định nghĩa của ta biết rằng có một nhân tử ,có nghĩa là số bội đại số của phải thỏa mãn .
Giả sử có các giá trị riêng phân biệt , trong đó số bội hình học của là . Ta có số bội hình học tổng cộng của ,
là số chiều của tổng của các không gian riêng của tất cả các giá trị riêng của , hay tương đương là số vectơ riêng độc lập tuyến tính tối đa của . Nếu thì
- Tổng trực tiếp của các không gian riêng của tất cả giá trị riêng là toàn bộ không gian vectơ .
- Một cơ sở của có thể được tạo ra từ vectơ riêng độc lập tuyến tính của ; một cơ sở như vậy được gọi là cơ sở riêng
- Mọi vectơ trong có thể được viết dưới dạng tổ hợp tuyến tính của các vectơ riêng của .
Các tính chất bổ sung của giá trị riêng
[sửa | sửa mã nguồn]Cho là ma trận vuông số phức với các trị riêng . Mỗi trị riêng dưới đây có thể lặp lại tới lần, trong đó là số bội đại số. Sau đây là các tính chất của ma trận và các giá trị riêng của nó:
- Vết của , được định nghĩa là tổng của các phần tử trên đường chéo chính của nó, cũng chính là tổng của các giá trị riêng
- Định thức của chính là tích của các giá trị riêng,
- Các giá trị riêng của lũy thừa bậc của ; tức là các giá trị riêng của với số nguyên dương bất kỳ , là .
- Ma trận khả nghịch khi và chỉ khi mỗi giá trị riêng của nó đều khác 0.
- Nếu khả nghịch thì các giá trị riêng của là và số bội hình học của mỗi giá trị riêng đều bằng nhau. Hơn nữa, các giá trị riêng cũng có cùng số bội đại số.
- Nếu bằng ma trận chuyển vị liên hợp phức , hay nếu là ma trận Hermite, thì mọi giá trị riêng đều là thực. Điều này cũng đúng với các ma trận đối xứng thực bất kỳ.
- Nếu không chỉ là ma trận Hermite mà còn là xác định dương, hay nửa xác định dương, xác định âm, hoặc nửa xác định âm thì mỗi giá trị riêng cũng tương ứng là đều dương, đều không âm, đều âm, hoặc đều không dương.
- Nếu là ma trận unita thì mỗi giá trị riêng có giá trị tuyệt đối .
- Nếu là một ma trận và là các giá trị riêng của nó thì các giá trị riêng của ma trận (trong đó là ma trận đơn vị) là . Hơn nữa nếu có số , các giá trị riêng của ma trận là . Tổng quát hơn nữa, với một hàm đa thức với biến ma trận ta có các giá trị riêng của ma trận là . Vậy là nghiệm của đa thức đặc trưng biến ma trận của chính nó.
Nhận xét: từ kết quả trên, ta nhận thấy có một cách để tính nhanh định thức . Đó là ta tìm đa thức đặc trưng của ma trận . Sau đó, tính giá trị của
Đặc trưng biến thiên
[sửa | sửa mã nguồn]Trong trường hợp ma trận Hermite, các giá trị riêng có thể được cho với một đặc trưng biến thiên. Giá trị riêng lớn nhất của ma trận Hermite là giá trị lớn nhất của dạng toàn phương . Một vectơ sao cho dạng toàn phương đạt giá trị lớn nhất đó, là một vectơ riêng.
Vectơ riêng trái và phải
[sửa | sửa mã nguồn]Nhiều lĩnh vực nghiên cứu biểu diễn các vectơ dưới dạng ma trận chỉ với một cột đơn hơn là ma trận với một hàng đơn. Vì lý do đó, từ "vectơ riêng" của một ma trận hầu như luôn đề cập đến vectơ riêng phải tức là một vectơ cột được nhân vào phía bên phải của một ma trận cỡ trong phương trình định nghĩa (1),
Tuy vậy, vấn đề vectơ riêng và giá trị riêng cũng có thể được định nghĩa cho các vectơ hàng được nhân trái với ma trận . Theo đó phương trình định nghĩa là
trong đó là một vô hướng và là ma trận hàng . Một vectơ hàng thỏa mãn phương trình này được gọi là một vectơ riêng trái của và là giá trị riêng tương ứng. Lấy chuyển vị của phương trình này ta có
So sánh với Phương trình (1), ta thấy ngay rằng một vectơ riêng trái của chính là chuyển vị của một vectơ riêng phải của , với cùng giá trị riêng. Hơn nữa, vì đa thức đặc trưng của cũng bằng đa thức đặc trưng của , giá trị riêng của các vectơ riêng trái của cũng bằng giá trị riêng của các vectơ riêng phải của .
Phân tích riêng và chéo hóa
[sửa | sửa mã nguồn]Giả sử các vectơ riêng của A tạo thành một cơ sở, hay tương đương là A có n vectơ riêng độc lập tuyến tính v1, v2, ..., vn tương ứng với các giá trị riêng λ1, λ2, ..., λn (không nhất thiết phân biệt). Định nghĩa một ma trận vuông Q có các cột là n vectơ riêng độc lập tuyến tính của A,
Vì mỗi cột của Q là một vectơ riêng của A, nhân phải Q với A chính là nhân mỗi cột của Q với các giá trị riêng tương ứng,
Định nghĩa một ma trận chéo Λ với các phần tử đường chéo Λii là các giá trị riêng tương ứng với cột thứ i của Q. Vậy thì
Vì mỗi cột của Q độc lập tuyến tính nên Q khả nghịch. Nhân phải mỗi vế của phương trình với Q−1,
hoặc nhân trái mỗi vế với Q−1, ta có
Vì vậy A có thể được phân tích thành tích của một ma trận với các cột là các vectơ riêng, một ma trận chéo với các giá trị riêng nằm trên đường chéo, và nghịch đảo của ma trận với vectơ riêng. Đây được gọi là phân tích riêng của ma trận và nó là một biến đổi đồng dạng. Một ma trận A như vậy được gọi là đồng dạng với ma trận chéo Λ hay chéo hóa được. Ma trận Q chính là ma trận chuyển cơ sở của phép biến đổi đồng dạng. Về cơ bản, hai ma trận A và Λ thể hiện cùng một biến đổi tuyến tính khi biểu diễn trong hai cơ sở khác nhau, trong đó các vectơ riêng được chọn làm cơ sở khi biểu diễn phép biến đổi dưới dạng ma trận Λ.
Bây giờ, giả sử ma trận A chéo hóa được. Cho P là một ma trận vuông không suy biến sao cho P−1AP là một ma trận đường chéo D. Nhân trái hai vế với P, ta được AP = PD. Mỗi cột của P vì thế phải là một vectơ riêng của A với giá trị riêng tương ứng là phần tử trên đường chéo của D. Vì các cột của P phải độc lập tuyến tính để P khả nghịch nên tồn tại n vectơ riêng độc lập tuyến tính của A. Vì vậy, suy ra các vectơ riêng của A tạo thành cơ sở khi và chỉ khi A là chéo hóa được.
Một ma trận không chéo hóa được thì được gọi là khiếm khuyết. Đối với các ma trận khiếm khuyết, ta có sự tổng quát hóa của các vectơ riêng trở thành các vectơ riêng tổng quát và ma trận chéo trở thành dạng chuẩn tắc Jordan. Trên một trường đại số đóng, một ma trận bất kỳ A luôn có dạng chuẩn tắc Jordan.
Đẳng thức giá trị riêng-vectơ riêng
[sửa | sửa mã nguồn]Đối với một ma trận Hermite, có thể tính bình phương của chuẩn của thành phần thứ j của một vectơ riêng đã chuẩn hóa, chỉ sử dụng các giá trị riêng của ma trận và các giá trị riêng của ma trận con tương ứng:
trong đó là ma trận con được tạo ra bằng cách bỏ đi các hàng và cột thứ j từ ma trận ban đầu.[36][37][38]
Giá trị riêng và hàm riêng của toán tử vi phân
[sửa | sửa mã nguồn]Định nghĩa giá trị riêng và vectơ riêng của một biến đổi tuyến tính T vẫn có thể áp dụng với trường hợp không gian vectơ là một không gian Hilbert hay không gian Banach vô hạn chiều. Một lớp các biến đổi tuyến tính trên không gian vô hạn chiều thường được sử dụng là các toán tử vi phân trên các không gian hàm. Cho D là một toán tử vi phân tuyến tính trên không gian các hàm khả vi vô hạn thực C∞ với đối số thực t. Phương trình định nghĩa giá trị riêng cho D là một phương trình vi phân
Các hàm thỏa mãn phương trình này chính là các vectơ riêng của D và thường được gọi là hàm riêng.
Ví dụ toán tử đạo hàm
[sửa | sửa mã nguồn]Xét toán tử đạo hàm với phương trình giá trị riêng
Phương trình vi phân này có thể được giải ra bằng cách nhân cả hai vế với dt/f(t) rồi lấy tích phân. Nghiệm của nó là hàm mũ
là một hàm riêng của toán tử đạo hàm. Trong trường hợp này hàm riêng chính là hàm của giá trị riêng tương ứng với nó. Đặc biệt, với λ = 0 hàm riêng f(t) là một hàm hằng.
Các ví dụ
[sửa | sửa mã nguồn]Ví dụ ma trận vuông cấp 2
[sửa | sửa mã nguồn]
Xét ma trận
Hình ảnh bên phải cho thấy tác động của phép biến đổi này lên các điểm tọa độ trong mặt phẳng. Các vectơ riêng v của phép biến đổi này thỏa mãn Phương trình (1), và các giá trị của λ sao cho định thức của ma trận (A − λI) bằng 0 là các giá trị riêng.
Lấy định thức để tìm đa thức đặc trưng của A,
Đặt cho phương trình đặc trưng bằng 0 và giải phương trình, nó có các nghiệm tại λ = 1 và λ = 3, cũng chính là hai giá trị riêng của ma trận A.
Với λ=1, từ Phương trình (2) ta có,
- ;
Mọi vectơ khác vectơ không với v1 = −v2 sẽ thỏa mãn phương trình này. Vì vậy,
là một vectơ riêng của A tương ứng với λ = 1, các bội vô hướng của vectơ này cũng vậy.
Với λ=3, Phương trình (2) trở thành
- ;
Mọi vectơ khác không với v1 = v2 thỏa mãn phương trình trên. Vì vậy,
và các bội vô hướng của nó là các vectơ riêng của A, ứng với λ = 3.
Vậy các vectơ vλ=1 và vλ=3 là các vectơ riêng của A tương ứng với các giá trị riêng λ=1 và λ=3.
Từ hình trên ta có thể thấy mỗi vectơ riêng không lệch khỏi span của nó.
Công thức tổng quát cho giá trị riêng của ma trận vuông cấp 2
[sửa | sửa mã nguồn]Giá trị riêng của một ma trận thực là[d]
Một cách biểu diễn khác là:
Chú ý các giá trị riêng luôn dương nếu b và c cùng dấu, do số hạng bên dưới dấu căn phải dương.
Ma trận vuông cấp 3
[sửa | sửa mã nguồn]Xét ma trận
Đa thức đặc trưng của A là
Các nghiệm của đa thức đặc trưng là 2, 1, và 11, cũng là ba giá trị riêng duy nhất của A. Các giá trị riêng này tương ứng với các vectơ riêng và , và bất kỳ các bội khác 0 của chúng.
Ma trận vuông cấp 3 với giá trị riêng phức
[sửa | sửa mã nguồn]Xét ma trận hoán vị cyclic sau
Ma trận này dịch chuyển mỗi tọa độ thứ hai và thứ ba của vectơ lên vị trí liền trước đó và chuyển tọa độ thứ nhất xuống vị trí cuối cùng.
Đa thức đặc trưng của nó là 1 − λ3, với các nghiệm
trong đó là đơn vị ảo với
Với giá trị riêng thực λ1 = 1, mỗi vectơ với ba thành phần của nó đều bằng nhau và khác 0 là vectơ riêng. Ví dụ,
Với cặp giá trị riêng liên hợp phức ta thấy,
Vậy
và
Vì vậy, hai vectơ riêng khác của A là phức, và tương ứng với giá trị riêng λ2 và λ3. Hai vectơ riêng phức cũng theo cặp liên hợp phức,
Ma trận khả nghịch
[sửa | sửa mã nguồn]Xét ma trận
Ta tìm cách biểu diễn ma trận nghịch đảo theo
Đa thức đặc trưng của ma trận là
có các giá trị riêng λ1 = −2, λ2 = 2, và λ3 = 3. Mọi giá trị riêng đều khác 0, vì thế khả nghịch.
Theo tính chất ở trên ta có:
- .
Do đó:
Đặt .
Ta có:
- .
Do đó khả nghịch và
Ma trận đường chéo
[sửa | sửa mã nguồn]Ma trận với chỉ với các phần tử nằm trên đường chéo chính được gọi là ma trận đường chéo. Các giá trị riêng của một ma trận chéo chính là các phần tử trên đường chéo chính. Xét ma trận
Đa thức đặc trưng của A là
nó có các nghiệm λ1 = 1, λ2 = 2, và λ3 = 3. Các nghiệm này là các giá trị riêng, cũng là các phần tử trên đường chéo chính của A.
Mỗi phần tử trên đường chéo tương ứng với một vectơ riêng với thành phần khác 0 duy nhất ở cùng hàng với phần tử đó. Trong ví dụ này, các giá trị riêng này tương ứng với các vectơ riêng có dạng sau ,
Ma trận tam giác
[sửa | sửa mã nguồn]Một ma trận vuông mà các phần tử ở nửa trên của đường chéo chính đều bằng 0 thì được gọi là ma trận tam giác dưới, trong khi một ma trận với các phần tử ở nửa dưới đường chéo chính đều bằng 0 được gọi là ma trận tam giác trên. Tương tự các ma trận chéo, các giá trị riêng của ma trận tam giác chính là các phần tử của đường chéo chính.
Xét ma trận tam giác dưới sau,
Đa thức đặc trưng của A là
có các nghiệm hay giá trị riêng là λ1 = 1, λ2 = 2, và λ3 = 3, cũng là các phần tử đường chéo của A.
Các giá trị riêng này tương ứng với các vectơ riêng có dạng sau (với c khác 0),
Ma trận với giá trị riêng lặp lại
[sửa | sửa mã nguồn]Tương tự ví dụ trước, ma trận tam giác dưới
có đa thức đặc trưng là mà nghiệm là các phần tử trên đường chéo,
Nghiệm của đa thức này, tức các giá trị riêng là 2 và 3. Số bội đại số của mỗi giá trị riêng này là 2; nói cách khác chúng đều là các nghiệm kép. Tổng số bội đại số của tất cả các giá trị riêng phân biệt là μA = 4 = n, luôn bằng bậc của đa thức đặc trưng hay số kích thước của ma trận A.
Mặt khác, số bội hình học của giá trị riêng 2 chỉ là 1, bởi không gian con riêng của nó được span bởi duy nhất một vectơ riêng nên chỉ có số chiều bằng 1. Tương tự, số bội hình học của giá trị riêng 3 cũng là 1 bởi không gian con riêng của nó được span bởi chỉ một vectơ riêng . Số bội hình học tổng cộng γA là 2, là giá trị số bội hình học nhỏ nhất có thể có của một ma trận với hai giá trị riêng khác nhau. Số bội hình học được định nghĩa tổng quát ở mục sau.
Định nghĩa tổng quát
[sửa | sửa mã nguồn]Khái niệm giá trị riêng và vectơ riêng được mở rộng một cách tự nhiên cho các biến đổi tuyến tính trên các không gian vectơ tùy ý. Cho V là một không gian vectơ bất kỳ trên một trường vô hướng K, và cho T là một tự đồng cấu tuyến tính từ V vào chính nó,
Ta gọi một vectơ v ∈ V khác vectơ không là một vectơ riêng của T khi và chỉ khi tồn tại vô hướng λ ∈ K sao cho
-
(5)
Phương trình này được gọi là phương trình (định nghĩa) giá trị riêng của T, và vô hướng λ được gọi là một giá trị riêng của T tương ứng với vectơ riêng v. T(v) là kết quả sau khi áp dụng biến đổi T lên vectơ v, còn λv là tích của vô hướng λ với vectơ v.[39][40]
Không gian con riêng, số bội hình học và cơ sở riêng
[sửa | sửa mã nguồn]Cho một giá trị riêng λ, xét tập hợp
đây là tập hợp tất cả vectơ riêng ứng với λ hợp với vectơ không. E được gọi là không gian con riêng hay không gian đặc trưng của T tương ứng với giá trị riêng λ.
Bởi định nghĩa của một biến đổi tuyến tính ta có,
với mọi cặp (x,y) ∈ V và α ∈ K. Vì thế, nếu u và v là các vectơ riêng của T tương ứng với giá trị riêng λ, tức là u,v ∈ E, thì
Vì vậy, cả u + v và αv hoặc là vectơ không hoặc là vectơ riêng của T tương ứng với λ, tức là u + v, αv ∈ E, và E là đóng đối với phép cộng vectơ và nhân vô hướng. Không gian con riêng E tương ứng với λ vì thế là một không gian con của V.[41] Nếu không gian con riêng đó có số chiều bằng 1, đôi khi nó được gọi là đường thẳng riêng.[42]
Số bội hình học γT(λ) của một giá trị riêng λ là số chiều của không gian con riêng ứng với λ, tức là số tối đa các vectơ riêng độc lập tuyến tính ứng với giá trị riêng đó.[10][29] Bởi định nghĩa của giá trị riêng và vectơ riêng, ta có γT(λ) ≥ 1 vì mỗi giá trị riêng đều ứng với ít nhất một vectơ riêng.
Các không gian con riêng của T luôn tạo thành một tổng trực tiếp. Hệ quả là các vectơ riêng ứng với các giá trị riêng khác nhau luôn là độc lập tuyến tính. Vì thế, tổng các số chiều của các không gian con riêng không thể vượt quá số chiều n của không gian vectơ V, và không thể có nhiều hơn n giá trị riêng khác nhau.[e]
Một không gian con bất kỳ được span bởi các vectơ riêng của T là một không gian con bất biến của T, sự thu hẹp của biến đổi T về không gian con đó là chéo hóa được. Hơn nữa, nếu các vectơ riêng của T có thể span toàn bộ không gian V, hay tương đương là V là tổng trực tiếp của các không gian con riêng tương ứng với mọi giá trị riêng của T, thì có thể lập một cơ sở của V từ các vectơ riêng độc lập tuyến tính của T được gọi là cơ sở riêng. Nếu T có một cơ sở riêng thì T được gọi là chéo hóa được.
Vectơ riêng là vectơ không
[sửa | sửa mã nguồn]Trong khi định nghĩa vectơ riêng sử dụng trong bài viết này loại trừ vectơ không, ta vẫn có thể định nghĩa giá trị riêng và vectơ riêng theo một cách mà vectơ không có thể là một vectơ riêng.[43]
Ta lại xét Phương trình định nghĩa (5). Định nghĩa giá trị riêng là bất kỳ vô hướng λ ∈ K sao cho tồn tại một vectơ khác không v ∈ V thỏa mãn (5). Cần chú ý rằng định nghĩa giá trị riêng theo cách này phải yêu cầu vectơ khác vectơ không, nếu không thì bất kỳ vô hướng nào trong K cũng sẽ là giá trị riêng của vectơ không. Định nghĩa vectơ riêng v tương ứng với giá trị riêng λ là một vectơ bất kỳ thỏa mãn (5) với λ được cho trước. Cho trước một giá trị riêng, vectơ không cũng là một vectơ thỏa mãn Phương trình (5), nên nó cũng là một vectơ riêng theo định nghĩa này.
Lý thuyết phổ
[sửa | sửa mã nguồn]Nếu λ là giá trị riêng của T, thì toán tử (T − λI) không là song ánh hay không tồn tại nghịch đảo (T − λI)−1. Mệnh đề đảo là đúng đối với trường hợp không gian vectơ hữu hạn chiều nhưng không đúng với vô hạn chiều. Tổng quát, toán tử tuyến tính (T − λI) có thể vẫn có nghịch đảo ngay cả khi λ không phải là giá trị riêng.
Vì lý do này, trong giải tích hàm các giá trị riêng có thể được tổng quát hóa thành phổ của một toán tử tuyến tính T tức là tập hợp tất cả các vô hướng λ sao cho toán tử (T − λI) không có nghịch đảo bị chặn. Phổ của một toán tử chứa tất cả các giá trị riêng nhưng không chỉ giới hạn ở chúng.
Đại số kết hợp và lý thuyết biểu diễn
[sửa | sửa mã nguồn]Ta có thể tổng quát hóa cấu trúc đại số tác động lên không gian vectơ, thay thế một toán tử tác động lên một không gian vectơ bằng một biểu diễn đại số – một đại số kết hợp tác động lên một mô đun. Nghiên cứu các tác động này là lĩnh vực của lý thuyết biểu diễn.
Khái niệm trọng số trong lý thuyết biểu diễn là một tương tự của khái niệm giá trị riêng, trong đó vectơ trọng số và không gian trọng số tương ứng là các tương tự của vectơ riêng và không gian con riêng.
Ứng dụng
[sửa | sửa mã nguồn]Giá trị riêng của các phép biến hình
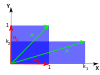
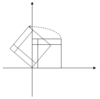
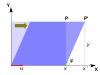
[sửa | sửa mã nguồn]Bảng dưới đây liệt kê các ví dụ về các phép biến đổi hình học trong mặt phẳng cùng các ma trận 2×2 của chúng và các giá trị riêng và vectơ riêng.
| Phép tỉ lệ | Phép tỉ lệ không đều | Phép quay | Phép trượt ngang | Phép quay hyperbolic | |
|---|---|---|---|---|---|
| Hình minh họa | 
|
|
|
 |

|
| Ma trận | |||||
| Đa thức
đặc trưng |
|||||
| Giá trị riêng, | |||||
| Số bội đại số, |
|||||
| Số bội hình học, |
|||||
| Vectơ riêng | Mọi vectơ khác
vectơ không |
Phương trình động lực
[sửa | sửa mã nguồn]Phương trình hiệu (công thức truy hồi) đơn giản nhất có dạng tuyến tính
- (a)
Các nghiệm của phương trình này là liên hệ tường minh của x theo t, có thể giải được từ phương trình đặc trưng
Để tìm phương trình đặc trưng, ta lập hệ k phương trình bao gồm phương trình thứ nhất là phương trình truy hồi (a) và k – 1 phương trình còn lại có dạng
, đây là hệ bậc nhất k chiều với vectơ biến
Tìm đa thức đặc trưng của ma trận của hệ rồi giải ra được k nghiệm đặc trưng để thay vào liên hệ tường minh
Một ví dụ điển hình là tìm công thức tổng quát của dãy Fibonacci.
Phương pháp tương tự cũng được dùng để giải một phương trình vi phân có dạng
Phương trình Schrödinger
[sửa | sửa mã nguồn]Một ví dụ về phương trình giá trị riêng mà biến đổi được biểu diễn dưới dạng một toán tử vi phân là phương trình Schrödinger không phụ thuộc thời gian trong cơ học lượng tử:
trong đó hay toán tử Hamilton, là một toán tử vi phân cấp 2 và , hàm sóng là một trong số các hàm riêng của nó tương ứng với giá trị riêng , được hiểu là năng lượng.
Tuy nhiên, trong trường hợp ta chỉ quan tâm đến các nghiệm trạng thái biên (bound state) của phương trình Schrödinger, ta tìm hàm riêng trong không gian các hàm khả tích bình phương. Bởi không gian này là một không gian Hilbert với tích vô hướng được định nghĩa, ta có thể xác định một tập cơ sở sao cho và có thể được biểu diễn tương ứng dưới dạng một mảng một chiều (tức là một vectơ) và một ma trận. Điều này cho phép biểu diễn phương trình Schrödinger dưới dạng ma trận.
Ký hiệu bra-ket thường được sử dụng trong ngữ cảnh này. Một vectơ biểu diễn trạng thái của một hệ, trong không gian Hilbert của các hàm khả tích bình phương được ký hiệu bởi . Với cách ký hiệu này, phương trình Schrödinger có thể viết là:
trong đó là một trạng thái riêng của , và biểu diễn cho giá trị riêng. là một toán tử tự liên hợp quan sát được, đây là khái niệm vô hạn chiều tương tự với ma trận Hermite. Giống trường hợp ma trận, trong phương trình trên, được hiểu là vectơ có được khi áp dụng biến đổi tác động lên .
Orbital phân tử
[sửa | sửa mã nguồn]Trong cơ học lượng tử, và đặc biệt là trong vật lý nguyên tử và phân tử, theo lý thuyết Hartree–Fock, các orbital của nguyên tử hay phân tử có thể được định nghĩa là các vectơ riêng của toán tử Fock. Các giá trị riêng tương ứng được hiểu là các thế ion hóa qua định lý Koopmans. Trong trường hợp này, thuật ngữ vectơ riêng được sử dụng với một ý nghĩa khá chung hơn, vì toán tử Fock phụ thuộc tường minh vào các orbital và các giá trị riêng của chúng. Vậy nếu ta muốn nhấn mạnh khía cạnh này, ta phải nói về các bài toán giá trị riêng phi tuyến tính. Những phương trình này thường được giải bằng một quá trình lặp, được gọi trong trường hợp này là phương pháp trường tự nhất quán. Trong hóa lượng tử, ta có thể biểu diễn phương trình Hartree–Fock trong một tập hàm cơ sở hóa học không trực giao. Biểu diễn này là một bài toán giá trị riêng tổng quát gọi là các phương trình Roothaan.
Phân tích thành phần chính
[sửa | sửa mã nguồn]
Phân tích riêng của một ma trận đối xứng nửa xác định dương hay PSD (positive semi-definite) thu được một cơ sở trực giao gồm các vectơ riêng, mỗi vectơ riêng có giá trị riêng tương ứng không âm. Phân tích trực giao của một ma trận PSD được sử dụng trong phân tích đa biến, trong đó các ma trận hiệp phương sai mẫu là PSD. Phép phân tích trực giao này được gọi là phép phân tích thành phần chính (PCA) trong thống kê. PCA nghiên cứu liên hệ tuyến tính giữa các biến. PCA được tiến hành trên ma trận hiệp phương sai hay ma trận tương quan (trong đó mỗi biến được tỉ lệ để có phương sai mẫu bằng 1). Đối với ma trận hiệp phương sai hay ma trận tương quan, các vectơ riêng tương ứng với các thành phần chính và các giá trị riêng tương ứng với phương sai giải thích bởi các thành phần chính. Phân tích thành phần chính của một ma trận tương quan cung cấp một cơ sở trực giao cho không gian của dữ liệu đã quan sát. Trong cơ sở này, các giá trị riêng lớn nhất tương ứng với các thành phần chính có liên hệ với tối đa hiệp phương sai trong một số dữ liệu đã quan sát.
Phép phân tích thành phần chính được sử dụng như một phương tiện để giảm chiều dữ liệu trong nghiên cứu các tập hợp dữ liệu lớn, chẳng hạn trong tin sinh học. Trong phương pháp luận Q, các giá trị riêng của ma trận tương quan xác định phán đoán về ý nghĩa thực tiễn của nhà phương pháp luận (khác với ý nghĩa thống kê trong kiểm định giả thuyết; xem tiêu chí xác định số nhân tố). Khái quát hơn, phân tích thành phần chính có thể được sử dụng làm phương pháp phân tích nhân tố trong mô hình phương trình cấu trúc (SEM).
Phân tích rung động
[sửa | sửa mã nguồn]Các bài toán giá trị riêng thường gặp trong lĩnh vực phân tích rung động của các cấu trúc cơ học với nhiều bậc tự do. Các giá trị riêng chính là các tần số tự nhiên (hay tần số riêng) của rung động, còn các vectơ riêng biểu diễn hình dạng của các mốt rung động. Cụ thể, rung động không cưỡng bức được mô tả bởi
hay
tức là gia tốc tỉ lệ với vị trí (ta sẽ có là hàm sin theo thời gian).
Trong chiều, trở thành ma trận khối lượng và là ma trận độ cứng.
Vậy các nghiệm được chọn là một tổ hợp tuyến tính của các nghiệm của bài toán giá trị riêng tổng quát sau
trong đó là giá trị riêng là tần số góc (ảo).
Hơn nữa, rung động cưỡng bức được cho bởi
dẫn đến một bài toán gọi là bài toán giá trị riêng bậc hai,
Có thể được đơn giản về một bài toán giá trị riêng tổng quát bằng các biến đổi đại số nhưng phải giải một hệ lớn hơn.
Tính trực giao của các vectơ riêng cho phép tách các phương trình vi phân sao cho hệ có thể được biểu diễn dưới dạng tổng tuyến tính của các vectơ riêng. Bài toán giá trị tổng quát của các cấu trúc phức tạp thường có thể được giải bằng phân tích phần tử hữu hạn.
Tenxơ mô men quán tính
[sửa | sửa mã nguồn]Trong cơ học, các vectơ riêng của tenxơ mô men quán tính xác định các trục chính của một vật rắn. Tenxơ mô men quán tính là một đại lượng quan trọng để xác định sự quay của một vật rắn quanh khối tâm của nó.
Tenxơ ứng suất
[sửa | sửa mã nguồn]Trong cơ học chất rắn, tenxơ ứng suất là đối xứng và vì thế có thể được phân tích thành một tenxơ đường chéo với các giá trị riêng nằm trên đường chéo và các vectơ riêng là một cơ sở. Vì nó là chéo nên theo định hướng này tenxơ ứng suất không có thành phần trượt; các thành phần nó có là các thành phần chính.
Đồ thị
[sửa | sửa mã nguồn]Trong lý thuyết phổ đồ thị, một giá trị riêng của một đồ thị được định nghĩa là giá trị riêng của ma trận kề của đồ thị đó, hay của ma trận Laplace của đồ thị dưới toán tử Laplace rời rạc. Vectơ riêng chính thứ của một đồ thị được định nghĩa là vectơ riêng ứng với giá trị riêng lớn thứ hoặc nhỏ thứ của ma trận Laplace. Vectơ riêng chính thứ nhất của đồ thị được gọi ngắn gọn là vectơ riêng chính.
Vectơ riêng chính được sử dụng để đo độ trung tâm của các đỉnh của nó. Một ví dụ là thuật toán PageRank của Google. Vectơ riêng chính của một ma trận kề được chỉnh sửa của đồ thị World Wide Web cho xếp hạng trang là các thành phần của nó. Vectơ này tương ứng với phân phối tĩnh của xích Markov được biểu diễn bởi ma trận kề đã được chuẩn hóa hàng. Tuy nhiên ma trận kề trước đó phải được chỉnh sửa để chắc rằng một phân phối tĩnh tồn tại. Vectơ riêng nhỏ thứ hai có thể được sử dụng để phân vùng đồ thị thành các cụm (cluster), qua phân vùng phổ hay các phương pháp có sẵn khác.
Xem thêm
[sửa | sửa mã nguồn]- Định lý phổ
- Phổ của ma trận
- Ma trận chéo hóa được
- Dạng chuẩn tắc Jordan
- Toán tử riêng
- Mặt phẳng riêng
- Giá trị suy biến
- Thuật toán giá trị riêng
- Trạng thái lượng tử riêng
- Tần số riêng
- Bài toán giá trị riêng bậc hai
- Giá trị riêng chuẩn tắc
Chú thích
[sửa | sửa mã nguồn]- ^ Note:
- In 1751, Leonhard Euler proved that any body has a principal axis of rotation: Leonhard Euler (presented: October 1751; published: 1760) "Du mouvement d'un corps solide quelconque lorsqu'il tourne autour d'un axe mobile" (On the movement of any solid body while it rotates around a moving axis), Histoire de l'Académie royale des sciences et des belles lettres de Berlin, pp. 176–227. On p. 212, Euler proves that any body contains a principal axis of rotation: "Théorem. 44. De quelque figure que soit le corps, on y peut toujours assigner un tel axe, qui passe par son centre de gravité, autour duquel le corps peut tourner librement & d'un mouvement uniforme." (Theorem. 44. Whatever be the shape of the body, one can always assign to it such an axis, which passes through its center of gravity, around which it can rotate freely and with a uniform motion.)
- In 1755, Johann Andreas Segner proved that any body has three principal axes of rotation: Johann Andreas Segner, Specimen theoriae turbinum [Essay on the theory of tops (i.e., rotating bodies)] (Halle ("Halae"), (Germany): Gebauer, 1755). (https://books.google.com/books?id=29 p. xxviiii [29]), Segner derives a third-degree equation in t, which proves that a body has three principal axes of rotation. He then states (on the same page): "Non autem repugnat tres esse eiusmodi positiones plani HM, quia in aequatione cubica radices tres esse possunt, et tres tangentis t valores." (However, it is not inconsistent [that there] be three such positions of the plane HM, because in cubic equations, [there] can be three roots, and three values of the tangent t.)
- The relevant passage of Segner's work was discussed briefly by Arthur Cayley. See: A. Cayley (1862) "Report on the progress of the solution of certain special problems of dynamics," Report of the Thirty-second meeting of the British Association for the Advancement of Science; held at Cambridge in October 1862, 32: 184–252; see especially pp. 225–226.
- ^ Kline 1972, pp. 807–808 Augustin Cauchy (1839) "Mémoire sur l'intégration des équations linéaires" (Memoir on the integration of linear equations), Comptes rendus, 8: 827–830, 845–865, 889–907, 931–937. From p. 827: "On sait d'ailleurs qu'en suivant la méthode de Lagrange, on obtient pour valeur générale de la variable prinicipale une fonction dans laquelle entrent avec la variable principale les racines d'une certaine équation que j'appellerai l'équation caractéristique, le degré de cette équation étant précisément l'order de l'équation différentielle qu'il s'agit d'intégrer." (One knows, moreover, that by following Lagrange's method, one obtains for the general value of the principal variable a function in which there appear, together with the principal variable, the roots of a certain equation that I will call the "characteristic equation", the degree of this equation being precisely the order of the differential equation that must be integrated.)
- ^ See:
- David Hilbert (1904) "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen. (Erste Mitteilung)" (Fundamentals of a general theory of linear integral equations. (First report)), Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (News of the Philosophical Society at Göttingen, mathematical-physical section), pp. 49–91. From p. 51: "Insbesondere in dieser ersten Mitteilung gelange ich zu Formeln, die die Entwickelung einer willkürlichen Funktion nach gewissen ausgezeichneten Funktionen, die ich 'Eigenfunktionen' nenne, liefern: …" (In particular, in this first report I arrive at formulas that provide the [series] development of an arbitrary function in terms of some distinctive functions, which I call eigenfunctions: … ) Later on the same page: "Dieser Erfolg ist wesentlich durch den Umstand bedingt, daß ich nicht, wie es bisher geschah, in erster Linie auf den Beweis für die Existenz der Eigenwerte ausgehe, … " (This success is mainly attributable to the fact that I do not, as it has happened until now, first of all aim at a proof of the existence of eigenvalues, … )
- For the origin and evolution of the terms eigenvalue, characteristic value, etc., see: Earliest Known Uses of Some of the Words of Mathematics (E)
- ^ Determine the characteristic polynomial of A: Use the quadratic formula to find the values of λ: Simplify radicand: Bring denominator into the square root:
- ^ For a proof of this lemma, see Roman 2008, Theorem 8.2 on p. 186; Shilov 1977, p. 109; Hefferon 2001, p. 364; Beezer 2006, Theorem EDELI on p. 469; and Lemma for linear independence of eigenvectors
Trích dẫn
[sửa | sửa mã nguồn]- ^ “Comprehensive List of Algebra Symbols”. Math Vault (bằng tiếng Anh). ngày 25 tháng 3 năm 2020. Truy cập ngày 19 tháng 8 năm 2020.
- ^ Burden & Faires 1993, tr. 401.
- ^ Herstein 1964, tr. 228, 229.
- ^ a b Nering 1970, tr. 38.
- ^ Weisstein, Eric W. “Eigenvalue”. mathworld.wolfram.com (bằng tiếng Anh). Truy cập ngày 19 tháng 8 năm 2020.
- ^ Betteridge 1965.
- ^ a b “Eigenvector and Eigenvalue”. www.mathsisfun.com. Truy cập ngày 19 tháng 8 năm 2020.
- ^ Press và đồng nghiệp 2007, tr. 536.
- ^ Wolfram.com: Eigenvector.
- ^ a b c d Nering 1970, tr. 107.
- ^ Hawkins 1975, §2.
- ^ a b c d Hawkins 1975, §3.
- ^ Kline 1972, p. 673.
- ^ a b Kline 1972, pp. 807–808.
- ^ Kline 1972, pp. 715–716.
- ^ Kline 1972, pp. 706–707.
- ^ Kline 1972, tr. 1063, p..
- ^ Aldrich 2006.
- ^ Francis 1961, tr. 265–271.
- ^ Kublanovskaya 1961, tr. 637–657.
- ^ Golub & Van Loan 1996, §7.3.
- ^ Meyer 2000, §7.3.
- ^ Cornell University Department of Mathematics (2016) Lower-Level Courses for Freshmen and Sophomores. Truy cập on 2016-03-27.
- ^ University of Michigan Mathematics (2016) Math Course Catalogue Lưu trữ 2015-11-01 tại Wayback Machine. Truy cập on 2016-03-27.
- ^ Herstein 1964, tr. 228,229.
- ^ Press và đồng nghiệp 2007, tr. 38.
- ^ a b Trefethen & Bau 1997.
- ^ Fraleigh 1976, tr. 358.
- ^ a b c Golub & Van Loan 1996, tr. 316.
- ^ Anton 1987, tr. 305,307.
- ^ a b Beauregard & Fraleigh 1973, tr. 307.
- ^ Herstein 1964, tr. 272.
- ^ Nering 1970, tr. 115–116.
- ^ Herstein 1964, tr. 290.
- ^ Nering 1970, tr. 116.
- ^ Wolchover 2019.
- ^ Denton và đồng nghiệp 2019.
- ^ Van Mieghem 2014.
- ^ Korn & Korn 2000, Section 14.3.5a.
- ^ Friedberg, Insel & Spence 1989, p. 217.
- ^ Nering 1970, tr. 107; Shilov 1977, tr. 109 Lemma for the eigenspace
- ^ Lipschutz & Lipson 2002, tr. 111.
- ^ Axler, tr. 77.
Tham khảo
[sửa | sửa mã nguồn]- Akivis, Max A.; Goldberg, Vladislav V. (1969), Tensor calculus, Russian, Science Publishers, Moscow
- Aldrich, John (2006), “Eigenvalue, eigenfunction, eigenvector, and related terms”, trong Miller, Jeff (biên tập), Earliest Known Uses of Some of the Words of Mathematics
- Alexandrov, Pavel S. (1968), Lecture notes in analytical geometry, Russian, Science Publishers, Moscow[thiếu ISBN]
- Anton, Howard (1987), Elementary Linear Algebra (ấn bản thứ 5), New York: Wiley, ISBN 0-471-84819-0
- Axler, Sheldon, Linear Algebra Done Right (ấn bản thứ 3), Springer, tr. 77, ISBN 978-3-319-30765-7
- Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Co., ISBN 0-395-14017-X
- Beezer, Robert A. (2006), A first course in linear algebra, Free online book under GNU licence, University of Puget Sound
- Benn, D.; Evans, D. (2004), A Practical Guide to the study of Glacial Sediments, London: Arnold, tr. 103–107
- Betteridge, Harold T. (1965), The New Cassell's German Dictionary, New York: Funk & Wagnall, LCCN 58-7924
- Bowen, Ray M.; Wang, Chao-Cheng (1980), Linear and multilinear algebra, Plenum Press, New York, ISBN 0-306-37508-7
- Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis (ấn bản thứ 5), Boston: Prindle, Weber and Schmidt, ISBN 0-534-93219-3
- Carter, Tamara A.; Tapia, Richard A.; Papaconstantinou, Anne, Linear Algebra: An Introduction to Linear Algebra for Pre-Calculus Students, Rice University, Online Edition, truy cập ngày 19 tháng 2 năm 2008
- Cohen-Tannoudji, Claude (1977), “Chapter II. The mathematical tools of quantum mechanics”, Quantum mechanics, John Wiley & Sons, ISBN 0-471-16432-1
- Curtis, Charles W. (1999), Linear Algebra: An Introductory Approach (ấn bản thứ 4), Springer, ISBN 0-387-90992-3
- Demmel, James W. (1997), Applied numerical linear algebra, SIAM, ISBN 0-89871-389-7
- Denton, Peter B.; Parke, Stephen J.; Tao, Terence; Zhang, Xining (ngày 10 tháng 8 năm 2019). "Eigenvectors from Eigenvalues: a survey of a basic identity in linear algebra". arΧiv:1908.03795 [math.RA].
- Diekmann O, Heesterbeek JA, Metz JA (1990), “On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations”, Journal of Mathematical Biology, 28 (4): 365–382, doi:10.1007/BF00178324, hdl:1874/8051, PMID 2117040, S2CID 22275430
- Fraleigh, John B. (1976), A First Course In Abstract Algebra (ấn bản thứ 2), Reading: Addison-Wesley, ISBN 0-201-01984-1
- Fraleigh, John B.; Beauregard, Raymond A. (1995), Linear algebra (ấn bản thứ 3), Addison-Wesley Publishing Company, ISBN 0-201-83999-7
- Francis, J. G. F. (1961), “The QR Transformation, I (part 1)”, The Computer Journal, 4 (3): 265–271, doi:10.1093/comjnl/4.3.265and Francis, J. G. F. (1962), “The QR Transformation, II (part 2)”, The Computer Journal, 4 (4): 332–345, doi:10.1093/comjnl/4.4.332
- Francis, J. G. F. (1962), “The QR Transformation, II (part 2)”, The Computer Journal, 4 (4): 332–345, doi:10.1093/comjnl/4.4.332
- Friedberg, Stephen H.; Insel, Arnold J.; Spence, Lawrence E. (1989), Linear algebra (ấn bản thứ 2), Englewood Cliffs, NJ: Prentice Hall, ISBN 0-13-537102-3
- Gelfand, I. M. (1971), Lecture notes in linear algebra, Russian, Science Publishers, Moscow
- Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2005), Indefinite linear algebra and applications, Basel, Boston, Berlin: Birkhäuser Verlag, ISBN 3-7643-7349-0
- Golub, Gene F.; van der Vorst, Henk A. (2000), “Eigenvalue computation in the 20th century” (PDF), Journal of Computational and Applied Mathematics, 123 (1–2): 35–65, Bibcode:2000JCoAM.123...35G, doi:10.1016/S0377-0427(00)00413-1
- Golub, Gene H.; Van Loan, Charles F. (1996), Matrix computations (ấn bản thứ 3), Baltimore, MD: Johns Hopkins University Press, ISBN 978-0-8018-5414-9
- Graham, D.; Midgley, N. (2000), “Graphical representation of particle shape using triangular diagrams: an Excel spreadsheet method”, Earth Surface Processes and Landforms, 25 (13): 1473–1477, Bibcode:2000ESPL...25.1473G, doi:10.1002/1096-9837(200012)25:13<1473::AID-ESP158>3.0.CO;2-C, S2CID 128825838
- Greub, Werner H. (1975), Linear Algebra (ấn bản thứ 4), New York: Springer-Verlag, ISBN 0-387-90110-8
- Halmos, Paul R. (1987), Finite-dimensional vector spaces (ấn bản thứ 8), New York: Springer-Verlag, ISBN 0-387-90093-4
- Hawkins, T. (1975), “Cauchy and the spectral theory of matrices”, Historia Mathematica, 2: 1–29, doi:10.1016/0315-0860(75)90032-4
- Heesterbeek, J. A. P.; Diekmann, Odo (2000), Mathematical epidemiology of infectious diseases, Wiley series in mathematical and computational biology, West Sussex, England: John Wiley & Sons[liên kết hỏng]
- Hefferon, Jim (2001), Linear Algebra, Colchester, VT: Online book, St Michael's College
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Horn, Roger A.; Johnson, Charles F. (1985), Matrix analysis, Cambridge University Press, ISBN 0-521-30586-1
- Kline, Morris (1972), Mathematical thought from ancient to modern times, Oxford University Press, ISBN 0-19-501496-0
- Knox-Robinson, C.; Gardoll, Stephen J. (1998), “GIS-stereoplot: an interactive stereonet plotting module for ArcView 3.0 geographic information system”, Computers & Geosciences, 24 (3): 243, Bibcode:1998CG.....24..243K, doi:10.1016/S0098-3004(97)00122-2
- Korn, Granino A.; Korn, Theresa M. (2000), “Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review”, New York: McGraw-Hill (ấn bản thứ 2), Bibcode:1968mhse.book.....K, ISBN 0-486-41147-8
- Kublanovskaya, Vera N. (1961), “On some algorithms for the solution of the complete eigenvalue problem”, USSR Computational Mathematics and Mathematical Physics, 3: 637–657. Also published in: “О некоторых алгорифмах для решения полной проблемы собственных значений” [On certain algorithms for the solution of the complete eigenvalue problem], Журнал вычислительной математики и математической физики (Journal of Computational Mathematics and Mathematical Physics) (bằng tiếng Nga), 1 (4): 555–570, 1961
- Kuttler, Kenneth (2007), An introduction to linear algebra (PDF), Brigham Young University, Bản gốc (PDF) lưu trữ ngày 7 tháng 8 năm 2008, truy cập ngày 1 tháng 3 năm 2021
- Lancaster, P. (1973), Matrix theory, Russian, Moscow: Science Publishers
- Larson, Ron; Edwards, Bruce H. (2003), Elementary linear algebra (ấn bản thứ 5), Houghton Mifflin Company, ISBN 0-618-33567-6
- Lipschutz, Seymour (1991), Schaum's outline of theory and problems of linear algebra, Schaum's outline series (ấn bản thứ 2), New York: McGraw-Hill Companies, ISBN 0-07-038007-4
- Lipschutz, Seymour; Lipson, Marc (ngày 12 tháng 8 năm 2002). Schaum's Easy Outline of Linear Algebra. McGraw Hill Professional. tr. 111. ISBN 978-007139880-0.
- Meyer, Carl D. (2000), Matrix analysis and applied linear algebra, Philadelphia: Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (ấn bản thứ 2), New York: Wiley, LCCN 76091646
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), Numerical Recipes: The Art of Scientific Computing (ấn bản thứ 3), ISBN 978-0521880688
- Roman, Steven (2008), Advanced linear algebra (ấn bản thứ 3), New York: Springer Science + Business Media, ISBN 978-0-387-72828-5
- Sharipov, Ruslan A. (1996), Course of Linear Algebra and Multidimensional Geometry: the textbook, arXiv:math/0405323, Bibcode:2004math......5323S, ISBN 5-7477-0099-5
- Shilov, Georgi E. (1977), Linear algebra, Translated and edited by Richard A. Silverman, New York: Dover Publications, ISBN 0-486-63518-X
- Shores, Thomas S. (2007), Applied linear algebra and matrix analysis, Springer Science+Business Media, ISBN 978-0-387-33194-2
- Sneed, E. D.; Folk, R. L. (1958), “Pebbles in the lower Colorado River, Texas, a study of particle morphogenesis”, Journal of Geology, 66 (2): 114–150, Bibcode:1958JG.....66..114S, doi:10.1086/626490, S2CID 129658242
- Strang, Gilbert (1993), Introduction to linear algebra, Wellesley, MA: Wellesley-Cambridge Press, ISBN 0-9614088-5-5
- Strang, Gilbert (2006), Linear algebra and its applications, Belmont, CA: Thomson, Brooks/Cole, ISBN 0-03-010567-6
- Trefethen, Lloyd N.; Bau, David (1997), Numerical Linear Algebra, SIAM
- Van Mieghem, Piet (ngày 18 tháng 1 năm 2014). "Graph eigenvectors, fundamental weights and centrality metrics for nodes in networks". arΧiv:1401.4580 [math.SP].
- Weisstein, Eric W. “Eigenvector”. mathworld.wolfram.com. Truy cập ngày 4 tháng 8 năm 2019.
- Wolchover, Natalie (ngày 13 tháng 11 năm 2019). “Neutrinos Lead to Unexpected Discovery in Basic Math”. Quanta Magazine. Truy cập ngày 27 tháng 11 năm 2019.
- Xirouhakis, A.; Votsis, G.; Delopoulus, A. (2004), Estimation of 3D motion and structure of human faces (PDF), National Technical University of Athens
- (tiếng Nga)Pigolkina, T. S.; Shulman, V. S. (1977). “Eigenvalue”. Trong Vinogradov, I. M. (biên tập). Mathematical Encyclopedia. 5. Moscow: Soviet Encyclopedia.
Liên kết ngoài
[sửa | sửa mã nguồn]- Vectơ riêng Lưu trữ 2022-01-28 tại Wayback Machine trên Từ điển bách khoa Việt Nam
- What are Eigen Values? – non-technical introduction from PhysLink.com's "Ask the Experts"
- Eigen Values and Eigen Vectors Numerical Examples – Tutorial and Interactive Program from Revoledu.
- Introduction to Eigen Vectors and Eigen Values – lecture from Khan Academy
- Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10 – A visual explanation with 3Blue1Brown
- Matrix Eigenvectors Calculator from Symbolab (Click on the bottom right button of the 2x12 grid to select a matrix size. Select an size (for a square matrix), then fill out the entries numerically and click on the Go button. It can accept complex numbers as well.)
- “A Beginner's Guide to Eigenvectors”. Deeplearning4j. 2015. Bản gốc lưu trữ ngày 21 tháng 7 năm 2018. Truy cập ngày 18 tháng 8 năm 2015.
- Hill, Roger (2009). “λ – Eigenvalues”. Sixty Symbols. Brady Haran for the University of Nottingham.
Theory
- Hazewinkel, Michiel biên tập (2001), “Eigen value”, Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4
- Hazewinkel, Michiel biên tập (2001), “Eigen vector”, Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4
- “Eigenvalue (of a matrix)”. PlanetMath.
- Eigenvector – Wolfram MathWorld
- Eigen Vector Examination working applet
- Same Eigen Vector Examination as above in a Flash demo with sound
- Computation of Eigenvalues
- Numerical solution of eigenvalue problems Edited by Zhaojun Bai, James Demmel, Jack Dongarra, Axel Ruhe, and Henk van der Vorst
- Eigenvalues and Eigenvectors on the Ask Dr. Math forums: [1], [2]
Demonstration applets

































































































![{\displaystyle {\bigl [}{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcacd8bee0f5c4d9f5e8e3fc2c4932447e0e2aec)
![{\displaystyle {\begin{aligned}|A-\lambda I|&=\left|{\begin{bmatrix}2&1\\1&2\end{bmatrix}}-\lambda {\begin{bmatrix}1&0\\0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &1\\1&2-\lambda \end{vmatrix}},\\[6pt]&=3-4\lambda +\lambda ^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/616c8bf6fe953c6bfbda5132efcdf799d4f13ced)











![{\displaystyle {\begin{aligned}|A-\lambda I|&=\left|{\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}-\lambda {\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &0&0\\0&3-\lambda &4\\0&4&9-\lambda \end{vmatrix}},\\[6pt]&=(2-\lambda ){\bigl [}(3-\lambda )(9-\lambda )-16{\bigr ]}=-\lambda ^{3}+14\lambda ^{2}-35\lambda +22.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30165fb86a7e23644d2e3373a1c2c68af4756523)














![{\displaystyle A=\left[{\begin{array}{rrr}1&-1&-1\\1&3&1\\-3&1&-1\\\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/160ce8500f42e89049e2829db98d81595cb99884)













































































