Logarit

Phép tính số học

Phép cộng (+) $\scriptstyle \left.{\begin{matrix}\scriptstyle {\text{số hạng}}\,+\,{\text{số hạng}}\\\scriptstyle {\text{hạng tử}}\,+\,{\text{hạng tử}}\\\scriptstyle {\text{số cộng}}\,+\,{\text{số cộng}}\end{matrix}}\right\}\,=\,$ $\scriptstyle {\text{tổng}}$ Phép trừ (−) $\scriptstyle {\text{số bị trừ}}\,-\,{\text{số trừ}}\,=\,$ $\scriptstyle {\text{hiệu}}$ Phép nhân (×) $\scriptstyle \left.{\begin{matrix}\scriptstyle {\text{thừa số}}\,\times \,{\text{thừa số}}\\\scriptstyle {\text{nhân tử}}\,\times \,{\text{nhân tử}}\end{matrix}}\right\}\,=\,$ $\scriptstyle {\text{tích}}$ Phép chia (÷) $\scriptstyle \left.{\begin{matrix}\scriptstyle {\frac {\scriptstyle {\text{số bị chia}}}{\scriptstyle {\text{số chia}}}}\\\scriptstyle {\text{ }}\\\scriptstyle {\frac {\scriptstyle {\text{tử số}}}{\scriptstyle {\text{mẫu số}}}}\end{matrix}}\right\}\,=\,$ ${\begin{matrix}\scriptstyle {\text{phân số}}\\\scriptstyle {\text{thương}}\\\scriptstyle {\text{tỷ số}}\end{matrix}}$ Lũy thừa $\scriptstyle {\text{cơ số}}^{\text{số mũ}}\,=\,$ $\scriptstyle {\text{lũy thừa}}$ Căn bậc n (√) $\scriptstyle {\sqrt[{\text{bậc}}]{\scriptstyle {\text{số dưới căn}}}}\,=\,$ $\scriptstyle {\text{căn}}$ Logarit (log) $\scriptstyle \log _{\text{cơ số}}({\text{số đối logarit}})\,=\,$ $\scriptstyle {\text{logarit}}$

Đồ thị của ba hàm số logarit phổ biến nhất. Các điểm đặc biệt log_b b = 1 được biểu diễn bằng đường đứt đoạn và cả ba đồ thị cắt nhau tại log_b 1 = 0.

Đồ thị của hàm logarit cơ số 2 cắt trục hoành tại x = 1 và đi qua các điểm (2, 1), (4, 2), và (8, 3), miêu tả rằng, chẳng hạn, log₂(8) = 3 và 2³ = 8. Khi x càng gần 0 thì đồ thị tiệm cận trục tung nhưng không giao với nó.

Trong toán học, logarit (tiếng Anh: logarithm) là hàm ngược của lũy thừa. Điều đó có nghĩa logarit của một số x là số mũ mà một giá trị cố định, gọi là cơ số b, phải được nâng lên lũy thừa để tạo ra số x đó. Trong trường hợp đơn giản nhất, logarit là đếm số lần lặp đi lặp lại của phép nhân; ví dụ, vì 1000 = 10 × 10 × 10 = 10³ nên logarit cơ số 10 của 1000 là 3 hay log₁₀(1000) = 3. Logarit cơ số b của x được ký hiệu là log_b (x), log_b x hay log x.

Tổng quát hơn, phép lũy thừa cho phép một số thực dương bất kỳ được nâng lên lũy thừa với một số mũ thực và kết quả thu được luôn là một số dương, do đó với hai số thực dương b và x bất kỳ, trong đó b khác 1, log_b (x) luôn có giá trị bằng một số thực y duy nhất. Một cách rõ ràng hơn, định nghĩa liên hệ giữa lũy thừa và logarit là:

$\log _{b}(x)=y$ khi và chỉ khi$\ b^{y}=x\$và $\ x>0$ và $\ b>0$ và$\ b\neq 1$.

Ví dụ, log₂ 64 = 6 vì 2⁶ = 64.

Logarit cơ số 10 (b = 10) được gọi là logarit thập phân và có nhiều ứng dụng trong khoa học và kỹ thuật. Logarit tự nhiên có cơ số là hằng số e (b ≈ 2,718), được ứng dụng phổ biến nhất trong toán học và vật lý vì tích phân và đạo hàm của nó đơn giản hơn. Logarit nhị phân sử dụng cơ số 2 (b = 2) và được sử dụng nhiều nhất trong khoa học máy tính. Logarit là một ví dụ về hàm lõm.

Logarit do John Napier giới thiệu lần đầu tiên vào năm 1614 như là một cách để đơn giản hóa việc tính toán. Về sau, nhiều nhà khoa học đã sử dụng nó để hỗ trợ trong tính toán, đặc biệt là các phép tính yêu cầu độ chính xác cao. Bằng cách sử dụng bảng số logarit, các phép nhân phức tạp với rất nhiều chữ số được thay bằng việc tra cứu bảng số và thực hiện các phép cộng đơn giản. Đó là vì logarit của một tích bằng tổng các logarit của các thừa số:

$\log _{b}(xy)=\log _{b}x+\log _{b}y,\,$

trong đó b, x và y đều là số dương và b ≠ 1. Thước loga, vốn được dựa trên logarit, cho phép tính nhanh mà không cần bảng số nhưng với độ chính xác thấp hơn. Ký hiệu logarit như ngày nay đến từ Leonhard Euler, người đã liên hệ nó với hàm mũ vào thế kỷ 18 và cũng là người tìm ra chữ e như là cơ số của logarit tự nhiên.

Thang đo logarit cho phép thu hẹp nhiều đại lượng về phạm vi nhỏ hơn. Chẳng hạn, decibel (dB) là đơn vị dùng để đưa tỷ lệ về logarit, phần lớn cho công suất tín hiệu và biên độ (trong đó có áp suất âm thanh). Trong hóa học, pH là chỉ số logarit để đo độ axit hay bazơ của dung dịch nước. Logarit cũng phổ biến trong công thức khoa học, trong việc nghiên cứu độ phức tạp của tính toán hay các phân dạng. Nó hỗ trợ mô tả tỷ lệ tần số của các quãng trong âm nhạc, xuất hiện trong công thức đếm số nguyên tố, tính gần đúng một giai thừa, nghiên cứu một số mô hình trong tâm vật lý học và trong lĩnh vực kế toán điều tra.

Logarit phức là hàm ngược của hàm lũy thừa trong số phức. Một dạng khác của logarit là logarit rời rạc và có ứng dụng trong mật mã hóa khóa công khai.

Ý tưởng và định nghĩa

Phép cộng, phép nhân và lũy thừa là ba trong những phép toán cơ bản nhất. Phép ngược lại của phép cộng là phép trừ: nếu ta cộng thêm 5 vào x để có x + 5, để đảo ngược thao tác này ta phải trừ x + 5 cho 5. Phép ngược lại của phép nhân là phép chia: nếu ta nhân x cho 5 để có 5x thì sau đó, ta phải chia 5x cho 5 để có x. Tương tự, logarit chính là phép toán ngược lại của lũy thừa. Lũy thừa là khi ta nâng một số lên một số mũ nhất định. Chẳng hạn, 2 nâng lên lũy thừa 3 bằng 8:

$2^{3}=2\times 2\times 2=8$

Trường hợp tổng quát là khi ta nâng một số b lên lũy thừa y để có x:

$b^{y}=x$

Số b ở đây được gọi là cơ số. Cơ số là số được nâng lên một số mũ nhất định, và trong ví dụ trên, cơ số này bằng 2. Để biểu diễn b theo x, ta lấy căn bậc y cả hai vế để có:

$b={\sqrt[{y}]{x}}$

Biểu diễn y theo x khó hơn rất nhiều, nhưng logarit cho phép ta thực hiện điều này:

$y=\log _{b}x$

Biểu thức trên có nghĩa y là lũy thừa mà ta cần phải nâng b lên để có được x. Đây là phép ngược lại của lũy thừa vì logarit của x cho biết số mũ mà cơ số được nâng lên.

Lũy thừa

Đề mục con này tóm tắt ngắn gọn về phép lũy thừa, một bước cơ bản để hiểu được bản chất của logarit. Nâng b lên lũy thừa n, với n là một số tự nhiên, tức là ta đã thực hiện phép nhân n thừa số với nhau, mỗi thừa số bằng b. Lũy thừa n của b được ký hiệu là bⁿ:

$b^{n}=\underbrace {b\times b\times \cdots \times b} _{n}$

Lũy thừa có thể được mở rộng thành dạng b^y, với b là một số dương và số mũ y là một số thực bất kỳ. Chẳng hạn b⁻¹ là nghịch đảo của b, hay bằng 1/b. Nâng b lên lũy thừa 1/2 thì được căn bậc hai của b.

Tổng quát hơn, khi nâng b lên lũy thừa hữu tỉ p/q với p và q là số nguyên, ta có:

$b^{p/q}={\sqrt[{q}]{b^{p}}},$

hay căn bậc q của $b^{p}\!\!$.

Cuối cùng, mỗi số vô tỉ y có thể được làm tròn để đưa về các số hữu tỉ. Sử dụng cách này, có thể tính được lũy thừa y của b: chẳng hạn ${\sqrt {2}}\approx 1,414...$ và $b^{\sqrt {2}}$ được tính gần đúng hơn theo dãy số $b^{1},b^{1,4},b^{1,41},b^{1,414},...$ Những thông tin chi tiết và các công thức có liên quan đều có trong bài viết về lũy thừa.

Định nghĩa

Logarit cơ số b của một số thực dương x là số mũ mà b cần phải được nâng lên để có được x. Nói cách khác, logarit cơ số b của x là nghiệm y của phương trình

$b^{y}=x$

và được ký hiệu là log_b x.

Trong phương trình y = log_b x, giá trị y là câu trả lời cho câu hỏi "b cần được nâng lên số mũ nào để có được x?".

Ví dụ

• log₂ 16 = 4 vì 2⁴ = 2 × 2 × 2 × 2 = 16.
• Logarit có thể là số âm:$\quad \log _{2}\!{\frac {1}{2}}=-1\quad$vì$\quad 2^{-1}={\frac {1}{2^{1}}}={\frac {1}{2}}.$
• log₁₀150 gần bằng 2,176, một số nằm giữa 2 và 3, giống như khi 150 nằm giữa 10² = 100 và 10³ = 1000.
• Với mọi cơ số b, log_b b = 1 và log_b 1 = 0 vì b¹ = b và b⁰ = 1.

Các đồng nhất thức logarit

Bài chi tiết: Danh sách đồng nhất thức logarit

Các công thức quan trọng sau đây, gọi là đồng nhất thức logarit, liên hệ các logarit với nhau.

Tích, thương, lũy thừa và căn

Logarit của một tích là tổng các logarit của các thừa số; logarit của một thương gồm hai số là hiệu logarit của hai số đó. Logarit của một số lũy thừa p bằng p lần logarit của số đó; logarit của căn bậc p là logarit của số đó chia cho p. Bảng dưới đây liệt kê các phép tính logarit cơ bản nêu trên và các ví dụ. Các đồng nhất thức đều có được sau khi thay $x=b^{\log _{b}x}$ hoặc $y=b^{\log _{b}y}$ ở vế trái của các biểu thức.

	Công thức	Ví dụ
Tích	$\log _{b}(xy)=\log _{b}x+\log _{b}y$	$\log _{3}243=\log _{3}(9\cdot 27)=\log _{3}9+\log _{3}27=2+3=5$
Thương	$\log _{b}\!{\frac {x}{y}}=\log _{b}x-\log _{b}y$	$\log _{2}16=\log _{2}\!{\frac {64}{4}}=\log _{2}64-\log _{2}4=6-2=4$
Lũy thừa	$\log _{b}\left(x^{p}\right)=p\log _{b}x$	$\log _{2}64=\log _{2}\left(2^{6}\right)=6\log _{2}2=6$
Căn	$\log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}x}{p}}$	$\log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1,5$

Đổi cơ số

Logarit log_bx có thể được tính từ logarit cơ số trung gian k của x và b theo công thức:

$\log _{b}x={\frac {\log _{k}x}{\log _{k}b}}.\,$

Giải thích phép tính logarit qua cơ số trung gian
Ta đã biết $x=b^{\log _{b}x}$. Lấy logarit logk cho cả hai vế của biểu thức, ta được $\log _{k}x=\log _{k}\left(b^{\log _{b}x}\right)=\log _{b}x\cdot \log _{k}b$. Chia cả hai vế cho $\log _{k}b$, ta được: $\log _{b}x={\frac {\log _{k}x}{\log _{k}b}}$, cho thấy hệ số quy đổi từ một giá trị $\log _{k}$ đã biết đến giá trị $\log _{b}$ tương ứng là $(\log _{k}b)^{-1}.$

Các máy tính bỏ túi điển hình thường tính logarit cơ số 10 và e. Logarit cơ số b bất kỳ có thể được xác định bằng cách đưa một trong hai logarit đặc biệt này vào công thức trên:

$\log _{b}x={\frac {\log _{10}x}{\log _{10}b}}={\frac {\log _{e}x}{\log _{e}b}}.\,$

Cho một số x và logarit cơ số b của nó log_bx với b chưa biết, thì b được tính bằng:

$b=x^{\frac {1}{\log _{b}x}},$

bằng cách mũ hóa biểu thức $x=b^{\log _{b}x}$ lên số mũ$\;{\tfrac {1}{\log _{b}x}}.$

Các cơ số thông dụng

Đồ thị của các hàm logarit cơ số 0,5, 2 và e

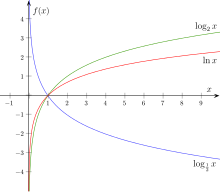
Trong các cơ số, có ba cơ số đặc biệt. Chúng gồm b = 10, b = e (hằng số vô tỉ xấp xỉ bằng 2,71828) và b = 2 (logarit nhị phân). Trong giải tích toán học, logarit cơ số e là phổ biến nhất nhờ các tính chất được giải thích dưới đây. Mặt khác, có thể dễ dàng tính logarit cơ số 10 trong hệ thập phân:

$\log _{10}(10x)=\log _{10}10+\log _{10}x=1+\log _{10}x.\$

Do đó, log₁₀x có liên hệ với số chữ số của một số nguyên dương x, đó là số nguyên nhỏ nhất lớn hơn log₁₀x. Chẳng hạn, log₁₀1430 gần bằng 3,15. Số nguyên liền sau là 4 và là số chữ số trong số 1430. Logarit tự nhiên và logarit nhị phân thường được dùng trong lý thuyết thông tin, có liên quan đến hai đơn vị cơ bản nhất trong thông tin là nat và bit. Logarit nhị phân cũng được sử dụng trong khoa học máy tính (hệ nhị phân); trong lý thuyết âm nhạc (quãng tám, đơn vị cent) và trong nhiếp ảnh để đo giá trị phơi sáng.

Bảng dưới đây liệt kê các ký hiệu logarit thông dụng và lĩnh vực mà chúng được sử dụng. Một số nơi viết logx thay vì log_bx, thậm chí ký hiệu ^blogx cũng tồn tại. Cột "Ký hiệu ISO" liệt kê các ký hiệu do Tổ chức tiêu chuẩn hóa quốc tế khuyến nghị (ISO 31-11). Ký hiệu log x được dùng chung cho cả ba cơ số tùy theo lĩnh vực: trong khoa học máy tính, log thường có nghĩa là log₂; trong toán học, log thường có nghĩa là log_e. Trong các trường hợp còn lại, log có nghĩa là log₁₀.

Cơ số b	Tên gọi của logbx	Ký hiệu ISO	Các ký hiệu khác	Sử dụng trong
2	logarit nhị phân	lb x	ld x, log x, lg x, log2x	khoa học máy tính, lý thuyết thông tin, lý thuyết âm nhạc, nhiếp ảnh
e	logarit tự nhiên	ln x	log x (trong toán học và nhiều ngôn ngữ lập trình)	toán học, vật lý, hóa học, thống kê, kinh tế học, lý thuyết thông tin và kỹ thuật
10	logarit thập phân	lg x	log x, log10x (trong kỹ thuật, sinh học, thiên văn học)	nhiều lĩnh vực trong kỹ thuật (xem decibel và xem dưới đây), bảng logarit, máy tính bỏ túi, phổ học

Lịch sử

Bài chi tiết: Lịch sử logarit

Lịch sử logarit bắt đầu vào thế kỷ 17 tại châu Âu, khi một hàm số mới được phát hiện ra đã làm mở rộng lĩnh vực giải tích vượt ra khỏi phạm vi tính toán đại số thông thường. Thuật ngữ logarit xuất hiện lần đầu tiên khi John Napier công bố cuốn sách Mirifici Logarithmorum Canonis Descriptio vào năm 1614. Trước Napier, đã có nhiều kỹ thuật khác với phạm vi tương tự, như prosthaphaeresis hay dùng bảng số (do Jost Bürgi phát triển khoảng năm 1600). Napier đề ra thuật ngữ logarit trong tiếng Latinh, logarithmorum xuất phát từ hai từ trong tiếng Hy Lạp: logos (tỷ số) và arithmos (số).

Logarit thập phân của một số là số mũ khi đưa số đó về dạng lũy thừa của 10, và Archimedes đã từng gọi nó là "bậc của một số". Những logarit thực đầu tiên là các phương pháp cảm tính để chuyển phép nhân thành phép cộng, tạo điều kiện để tính toán nhanh chóng. Một vài trong số đó có áp dụng bảng số được suy ra từ các đẳng thức lượng giác và được gọi chung là prosthaphaeresis.

Quá trình tìm ra một hàm số, sau này được gọi là logarit tự nhiên, bắt đầu khi Grégoire de Saint-Vincent, một tu sĩ Dòng Tên người Bỉ sống tại Prague, cố gắng xác định cầu phương của một hyperbol vuông. Archimedes đã viết cuốn The Quadrature of the Parabola vào thế kỷ 3 trước Công nguyên, nhưng người ta vẫn chưa biết được cầu phương của hyperbol đến khi Saint-Vincent công bố kết quả vào năm 1647. Sự liên quan của logarit giữa cấp số nhân và cấp số cộng đã thúc đẩy A. A. de Sarasa liên kết cầu phương của Saint-Vincent và logarit trong prosthaphaeresis, dẫn đến thuật ngữ "logarit hyperbol", một thuật ngữ đồng nghĩa với logarit tự nhiên. Về sau, hàm số mới này được Christiaan Huygens và James Gregory đánh giá cao. Ký hiệu log y do Leibniz tìm ra vào năm 1675 và một năm sau, ông liên hệ nó với tích phân $\int {\frac {dy}{y}}.$

Bảng logarit, thước loga và ứng dụng lịch sử

Khái niệm logarit trong Encyclopædia Britannica (năm 1797)

Bằng cách đơn giản hóa các phép tính phức tạp trước khi máy tính ra đời, logarit đóng góp đáng kể cho sự phát triển của khoa học, đặc biệt là thiên văn học. Nó cũng đóng góp cho sự tiến bộ của khảo sát xây dựng, hàng hải thiên văn và nhiều lĩnh vực khác. Pierre-Simon Laplace đã gọi logarit là

"...[một] thủ thuật đáng ngưỡng mộ mà, bằng cách rút ngắn một công việc vài tháng xuống vài ngày, nhân đôi cuộc đời của một nhà thiên văn, và loại bỏ những sai sót ghê tởm không thể tách rời từ những phép tính dài."

Vì hàm f(x) = b^x là hàm nghịch đảo của log_b x nên nó còn được gọi là antilogarit.

Bảng log

Một công cụ góp phần lớn trong việc ứng dụng logarit vào thực tế là bảng logarit. Bảng đầu tiên như vậy do Henry Briggs biên soạn năm 1617 ngay sau phát minh của Napier, sử dụng cơ số 10. Bảng đầu tiên của Briggs chứa logarit thập phân của tất cả các số nguyên từ 1 đến 1000, với độ chính xác đến 14 chữ số, tiếp đó là các bảng số trong phạm vi lớn hơn. Các bảng số này liệt kê các giá trị của log₁₀x với mỗi số x nằm trong một giới hạn nhất định. Logarit cơ số 10 được sử dụng nhiều nhất trong tính toán, dẫn đến thuật ngữ logarit thập phân, vì logarit của các số sai khác nhau 10 lần khác nhau bởi các số nguyên. Logarit thập phân của x có thể được chia thành phần nguyên logarit và phần thập phân logarit. Bảng logarit chỉ chứa phần thập phân logarit, vì dễ dàng xác định được phần nguyên logarit bằng cách đếm số chữ số từ dấu thập phân. Phần nguyên logarit của 10 · x là 1 cộng cho phần nguyên logarit của x, còn phần thập phân logarit là giống nhau. Bằng cách sử dụng bảng logarit ba chữ số, logarit của 3542 được ước lượng bởi

$\log _{10}3542=\log _{10}(1000\cdot 3,542)=3+\log _{10}3,542\approx 3+\log _{10}3,54\,$

Nếu dùng nội suy thì độ chính xác cao hơn nhiều:

$\log _{10}3542\approx 3+\log _{10}3,54+0,2(\log _{10}3,55-\log _{10}3,54)\$

Giá trị của 10^x có thể được xác định bằng cách tra cứu ngược lại từ bảng số trên, vì logarit là một hàm số đơn điệu.

Tính toán

Tích và thương của hai số dương c và d thường được tính bằng tổng và hiệu các logarit của chúng. Tích cd hoặc thương c/d có được bằng cách tra cứu antilogarit của tổng và tích đó trong cùng bảng số:

$cd=10^{\log _{10}c}\,10^{\log _{10}d}=10^{\log _{10}c+\log _{10}d}\,$

và

${\frac {c}{d}}=cd^{-1}=10^{\log _{10}c-\log _{10}d}.\,$

Đối với các phép tính toán thông thường, nếu yêu cầu độ chính xác cao, việc tra cứu hai logarit, tính tổng hoặc hiệu của chúng rồi tra cứu antilogarit nhanh hơn rất nhiều so với khi nhân bằng các công cụ trước đây như prosthaphaeresis (vốn phụ thuộc vào đẳng thức lượng giác).

Phép tính lũy thừa và căn được đưa về phép nhân hoặc chia và tra cứu bởi

$c^{d}=\left(10^{\log _{10}c}\right)^{d}=10^{d\log _{10}c}\,$

và

${\sqrt[{d}]{c}}=c^{\frac {1}{d}}=10^{{\frac {1}{d}}\log _{10}c}.\,$

Các bảng số chứa logarit thập phân của các hàm lượng giác tạo điều kiện thuận lợi cho việc tính toán lượng giác.

Thước loga

Một ứng dụng quan trọng khác của logarit là thước loga, một cặp thước chia độ theo logarit được sử dụng trong tính toán. Tiền thân của nó, thước Gunter, được phát minh ngay sau công bố của Napier. William Oughtred sau đó đã phát triển nó lên thành thước loga, một cặp thước logarit có thể trượt lẫn nhau. Các số được đặt trên thước với khoảng cách về độ dài tỷ lệ thuận với hiệu các logarit của chúng. Khi trượt thước bên trên tức là ta đã cộng cơ học các logarit với nhau như hình minh họa:

Sơ đồ miêu tả thước loga. Bắt đầu từ vị trí 2 ở thước bên dưới, cộng khoảng cách đến 3 ở thước bên trên để đạt tích bằng 6. Thước loga hoạt động được vì nó được chia độ sao cho khoảng cách từ 1 đến x tỷ lệ thuận với logarit của x.

Ví dụ, cộng khoảng cách từ 1 đến 2 ở thước bên dưới với khoảng cách từ 1 đến 3 ở thước bên trên cho tích của chúng bằng 6. Thước loga từng là một công cụ tính toán thiết yếu của các nhà khoa học cho đến những năm 1970, vì nó cho phép tính toán nhanh hơn nhiều so với kỹ thuật tra bảng số.

Tính chất trong giải tích

Người ta nghiên cứu sâu hơn về logarit thông qua khái niệm hàm số. Hàm số là quy tắc cho một số tuơng ứng với một số khác. Ví dụ, hàm số cho lũy thừa bậc x của b từ bất kỳ số thực x nào với b là cơ số được viết là $f(x)=b^{x}.\,$

Hàm số logarit

Ta đã biết phuơng trình

$b^{x}=y\,$

có một nghiệm x duy nhất (với y và b duơng, b khác 1). Để chứng minh điều này, ta cần liên hệ đến định lý giá trị trung gian trong giải tích. Theo định lý, một hàm số liên tục cho hai giá trị m và n cũng cho bất kỳ giá trị nào nằm giữa m và n. Hàm số liên tục là hàm mà đồ thị của nó có thể được vẽ trên mặt phẳng tọa độ mà không cần nhấc bút lên.

Tính chất này được xem là đúng với hàm f(x) = b^x. Vì f có thể mang giá trị duơng lớn hay nhỏ tùy ý, nên mỗi số y > 0 đều nằm giữa f(x₀) và f(x₁) với x₀ và x₁ thích hợp. Do đó, định lý giá trị trung gian cho thấy phuơng trình f(x) = y có một nghiệm. Nghiệm này là duy nhất vì hàm số f là hàm số tăng nếu b > 1 và là hàm số giảm nếu 0 < b < 1. Nghiệm x đó chính là logarit cơ số b của y, log_by. Hàm số như trên được gọi là hàm số logarit.

Hàm số log_bx được biểu thị bởi công thức

$\log _{b}(xy)=\log _{b}x+\log _{b}y.$

Nói đúng hơn, logarit cơ số b > 1 là hàm số tăng f duy nhất từ số thực dương đến số thực thỏa mãn f(b) = 1 và

$f(xy)=f(x)+f(y).$

Hàm ngược

Đồ thị của hàm logarit log_b(x) (màu xanh) đối xứng với đồ thị của hàm mũ b^x (màu đỏ) theo đường thẳng x = y.

Công thức tính lũy thừa cho thấy với một số x bất kỳ,

$\log _{b}\left(b^{x}\right)=x\log _{b}b=x.$

Lần lượt lấy lũy thừa bậc x của b rồi lấy logarit cơ số b, ta lại có được x. Ngược lại, với một số duơng y bất kỳ, biểu thức

$b^{\log _{b}y}=y$

cho thấy khi lấy logarit rồi lấy lũy thừa, ta lại có được y. Ta thấy khi đồng thời thực hiện phép lấy lũy thừa rồi lấy logarit trong cùng một biểu thức, ta có được biểu thức ban đầu. Vì vậy, logarit cơ số b là hàm ngược của f(x) = b^x.

Hàm ngược có liên hệ mật thiết với hàm số gốc của nó. Đồ thị của chúng đối xứng nhau qua đường thẳng x = y như hình bên phải: một điểm (t, u = b^t) trong đồ thị của f tuơng ứng với điểm (u, t = log_bu) trong đồ thị của hàm logarit và ngược lại. Như vậy, log_b(x) tiến lên vô hạn (lớn hơn bất kỳ số nào đã biết) nếu x tiến lên vô hạn, với b lớn hơn 1. Trong trường hợp này, log_b(x) là hàm số tăng. Khi b < 1 thì log_b(x) dần về âm vô hạn. Khi x dần về 0 thì giới hạn của log_bx là âm vô hạn với b > 1 và là duơng vô hạn với b < 1.

Đạo hàm và nguyên hàm

Đồ thị của hàm logarit tự nhiên (màu xanh lá) và tiếp tuyến của nó tại x = 1,5 (màu đen)

Các hàm số ngược nhau đều có tính chất giống nhau. f(x) = b^x là một hàm số liên tục và khả vi, và log_by cũng vậy. Thông thường, một hàm số liên tục là hàm số khả vi nếu đồ thị của nó không bị "đứt gãy" ở bất cứ điểm nào. Hơn nữa, vì đạo hàm của f(x) bằng ln(b)b^x theo tính chất của hàm mũ nên theo quy tắc hàm hợp, đạo hàm của log_bx được tính bằng

${\frac {d}{dx}}\log _{b}x={\frac {1}{x\ln b}},$

có nghĩa là hệ số góc của tiếp tuyến đồ thị hàm logarit cơ số b tại điểm (x, log_b(x)) bằng 1/(x ln(b)).

Đạo hàm của ln(x) là 1/x, nghĩa là ln(x) là nguyên hàm duy nhất của 1/x có giá trị 0 tại x = 1. Hàm số này còn được gọi là logarit tự nhiên, và đây cũng là một trong những lý do để giải thích tầm quan trọng của hằng số e.

Đạo hàm của hàm đối số tổng quát f(x) là

${\frac {d}{dx}}\ln f(x)={\frac {f'(x)}{f(x)}}.$

Tỷ số ở vế phải được gọi là đạo hàm logarit của f(x). Việc tính f'(x) theo đạo hàm của ln(f(x)) được gọi là vi phân logarit. Nguyên hàm của hàm logarit tự nhiên ln(x) là:

$\int \ln(x)\,dx=x\ln(x)-x+C.$

Từ phuơng trình này, có thể suy ra các biểu thức liên quan chẳng hạn như nguyên hàm của logarit cơ số khác bằng phép đổi cơ số.

Tích phân của hàm số logarit tự nhiên

Logarit tự nhiên của t là diện tích phần hình được tô đậm nằm dưới đồ thị hàm số f(x) = 1/x (nghịch đảo của x).

Logarit tự nhiên của t bằng tích phân của 1/x dx từ 1 đến t:

$\ln(t)=\int _{1}^{t}{\frac {1}{x}}\,dx.$

Nói cách khác, ln(t) là diện tích của hình phẳng giới hạn bởi trục hoành và đồ thị của hàm số 1/x, từ x = 1 đến x = t (hình bên phải). Đó là hệ quả từ việc áp dụng định lý cơ bản của giải tích và việc đạo hàm của ln(x) là 1/x. Vế phải của biểu thức trên có thể được xem như là khái niệm về logarit tự nhiên. Các công thức mũ và tích logarit đều được suy ra từ khái niệm này. Chẳng hạn, ta có công thức tích ln(tu) = ln(t) + ln(u) vì

$\ln(tu)=\int _{1}^{tu}{\frac {1}{x}}\,dx\ {\stackrel {(1)}{=}}\int _{1}^{t}{\frac {1}{x}}\,dx+\int _{t}^{tu}{\frac {1}{x}}\,dx\ {\stackrel {(2)}{=}}\ln(t)+\int _{1}^{u}{\frac {1}{w}}\,dw=\ln(t)+\ln(u).$

Phép biến đổi (1) là phép tính tích phân từng phần, còn phép biến đổi (2) là phép đổi biến số (w = x/t). Trong hình dưới đây, phép tính từng phần này tức là chia hình phẳng thành hai phần màu vàng và màu xanh. Thay đổi kích thước phần hình phẳng màu xanh bên trái theo hàng dọc và thu nhỏ lại nó theo hàng ngang theo biến t không làm thay đổi diện tích của nó. Di chuyển phần hình màu xanh một cách thích hợp thì nó lại khớp với đồ thị hàm số f(x) = 1/x. Do đó, phần hình phẳng màu xanh bên trái, tức là tích phân của f(x) từ t đến tu bằng tích phân từ 1 đến u. Đây chính là hình ảnh để minh họa phép biến đổi (2) một cách trực quan.

Hình ảnh minh họa công thức tích của logarit tự nhiên

Chứng minh tuơng tự, ta cũng có công thức lũy thừa ln(t^r) = r ln(t):

$\ln(t^{r})=\int _{1}^{t^{r}}{\frac {1}{x}}dx=\int _{1}^{t}{\frac {1}{w^{r}}}\left(rw^{r-1}\,dw\right)=r\int _{1}^{t}{\frac {1}{w}}\,dw=r\ln(t).$

Phép biến đổi thứ hai có sự thay đổi biến số w = x^1/r.

Tổng của dãy nghịch đảo các số tự nhiên,

$1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}},$

được gọi là chuỗi điều hòa. Nó có liên hệ với logarit tự nhiên: khi n tiến đến vô hạn thì hiệu

$\sum _{k=1}^{n}{\frac {1}{k}}-\ln(n)$

hội tụ về một số được gọi là hằng số Euler–Mascheroni γ = 0,5772.... Mối liên hệ này có vai trò trong việc phân tích các thuật toán, chẳng hạn như sắp xếp nhanh.

Một số tích phân khác của logarit tự nhiên cũng có ích trong nhiều trường hợp:

$\ln(x)=-\lim _{\epsilon \to 0}\int _{\epsilon }^{\infty }{\frac {dt}{t}}\left(e^{-xt}-e^{-t}\right)$

$\ln(x)=\int _{0}^{\infty }\,{\frac {dt}{t}}\,\left[\cos(t)-\cos(xt)\right]$

Đẳng thức đầu tiên được chứng minh vì nó có cùng một giá trị tại x = 1 và có cùng đạo hàm. Đẳng thức thứ hai được chứng minh bằng cách đặt

${\frac {1}{t}}=\int _{0}^{\infty }\,dq\,e^{-qt}$

rồi áp dụng phép biến đổi Laplace cho cos(xt) và cos(t).

Tính siêu việt của logarit

Số thực không phải là số đại số được gọi là số siêu việt. π và e là hai số như vậy, còn ${\sqrt {2-{\sqrt {3}}}}$ không phải là số siêu việt. Hầu hết số thực đều là số siêu việt. Logarit là một ví dụ về một hàm số siêu việt. Định lý Gelfond–Schneider khẳng định rằng logarit thường cho các giá trị siêu việt.

Tính toán

Các phím logarit (LOG cho cơ số 10 và LN cho cơ số e) trong một máy tính bỏ túi TI-83 Plus

Người ta có thể dễ dàng tính được logarit trong một số trường hợp, chẳng hạn như log₁₀(1000) = 3. Thông thường, logarit được tính bằng chuỗi lũy thừa hoặc trung bình hình học–đại số, hoặc tra cứu trong bảng số logarit tính sẵn với độ chính xác nhất định. Phương pháp Newton, một phương pháp lặp đi lặp lại để tìm nghiệm gần đúng của một phương trình, cũng có thể được sử dụng để tính logarit, vì hàm ngược của nó (hàm mũ) có thể được tính một cách hiệu quả. Thông qua bảng số, các phương pháp tương tự như CORDIC có thể được dùng để tính logarit chỉ qua phép cộng và phép dịch số học. Hơn nữa, thuật toán logarit nhị phân tính lb(x) một cách đệ quy, dựa vào phép bình phương x lặp đi lặp lại và áp dụng biểu thức

$\log _{2}\left(x^{2}\right)=2\log _{2}|x|.$

Chuỗi lũy thừa

Chuỗi Taylor

Chuỗi Taylor của ln(z) có tâm tại z = 1. Hình ảnh động này gồm 10 xấp xỉ đầu tiên cùng xấp xỉ thứ 99 và 100. Các xấp xỉ này không hội tụ ngoài khoảng cách 1 đơn vị từ tâm.

Với mỗi số thực z thỏa mãn 0 < z < 2, ta có:

${\begin{aligned}\ln(z)&={\frac {(z-1)^{1}}{1}}-{\frac {(z-1)^{2}}{2}}+{\frac {(z-1)^{3}}{3}}-{\frac {(z-1)^{4}}{4}}+\cdots \\&=\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {(z-1)^{k}}{k}}\end{aligned}}$

Ta cũng nói rằng ln(z) có thể được tính gần đúng theo dãy biểu thức

${\begin{array}{lllll}(z-1)&&\\(z-1)&-&{\frac {(z-1)^{2}}{2}}&\\(z-1)&-&{\frac {(z-1)^{2}}{2}}&+&{\frac {(z-1)^{3}}{3}}\\\vdots &\end{array}}$

Ví dụ, với z = 1,5, biểu thức thứ ba cho kết quả là 0,4167, lớn hơn khoảng 0,011 so với ln(1,5) = 0,405465. Chuỗi này ước lượng ln(z) với độ chính xác tùy ý, miễn rằng số hạng tử là đủ lớn. Trong giải tích, ln(z) còn được gọi là giới hạn của chuỗi. Nó là chuỗi Taylor của logarit tự nhiên tại z = 1. Từ chuỗi Taylor của ln(z), có thể suy ra phép tính gần đúng ln(1 + z) khi z nhỏ, |z| < 1, vì khi đó

$\ln(1+z)=z-{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}\cdots \approx z.$

Ví dụ, với z = 0,1, phép xấp xỉ bậc nhất cho kết quả ln(1,1) ≈ 0,1, có sai số dưới 5% so với giá trị chính xác, 0,0953.

Các chuỗi lũy thừa khác

Một chuỗi khác được dựa trên hàm hyperbolic ngược:

$\ln(z)=2\cdot \operatorname {artanh} \,{\frac {z-1}{z+1}}=2\left({\frac {z-1}{z+1}}+{\frac {1}{3}}{\left({\frac {z-1}{z+1}}\right)}^{3}+{\frac {1}{5}}{\left({\frac {z-1}{z+1}}\right)}^{5}+\cdots \right),$

với mỗi số thực z > 0. Sử dụng ký hiệu sigma, chuỗi trên có thể được viết lại thành:

$\ln(z)=2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {z-1}{z+1}}\right)^{2k+1}.$

Chuỗi trên được suy ra từ chuỗi Taylor. Nó hội tụ nhanh hơn nhiều so với chuỗi Taylor, nhất là khi z gần bằng 1. Chẳng hạn, với z = 1,5, ba hạng tử đầu tiên của chuỗi tính được gần đúng ln(1,5) với sai số khoảng 3×10⁻⁶. Tính hội tụ nhanh chóng khi z gần bằng 1 có thể được tận dụng theo cách sau: cho một xấp xỉ y ≈ ln(z) với độ chính xác thấp và đặt

$A={\frac {z}{\exp(y)}},\,$

logarit của z là:

$\ln(z)=y+\ln(A).\,$

Nếu giá trị y càng gần đúng thì giá trị A càng gần 1, do đó có thể tính logarit của nó một cách hiệu quả. A có thể được tính qua chuỗi lũy thừa, vốn hội tụ nhanh khi y không quá lớn. Với z lớn, người ta viết z = a · 10^b, khi đó ln(z) = ln(a) + b · ln(10).

Một phuơng pháp có liên quan có thể được dùng để tính logarit của số nguyên. Thay $\textstyle z={\frac {n+1}{n}}$ trong chuỗi trên, ta có

$\ln(n+1)=\ln(n)+2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {1}{2n+1}}\right)^{2k+1}.$

Nếu ta đã biết logarit của một số nguyên n lớn thì chuỗi này hội tụ rất nhanh với tốc độ là ${\frac {1}{2n+1}}$.

Trung bình hình học–đại số

Trung bình hình học–đại số cho phép tính gần đúng logarit tự nhiên với độ chính xác rất cao. Theo Sasaki & Kanda (1982), phương pháp này đặc biệt nhanh với sai số khoảng 400 đến 1000 chữ số thập phân, trong khi phương pháp dùng chuỗi Taylor thường nhanh chóng hơn nếu không đòi hỏi độ chính xác cao. Trong công trình của họ ln(x) được ước lượng với sai số 2^−p theo công thức sau (bởi Carl Friedrich Gauss):

$\ln(x)\approx {\frac {\pi }{2M(1,2^{2-m}/x)}}-m\ln(2).$

Ở đây M(x,y) chỉ trung bình hình học–đại số của x và y, có được bằng cách thực hiện lặp đi lặp lại các phép tính $(x+y)/2$ (trung bình cộng) và ${\sqrt {xy}}$ (trung bình nhân) rồi lấy hai kết quả thu được làm giá trị mới của x và y. Hai số này nhanh chóng hội tụ lại về một giới hạn, và giới hạn đó là giá trị của M(x,y). Giá trị m được chọn sao cho

$x\,2^{m}>2^{p/2}$

để đảm bảo độ chính xác cần thiết. Nếu m càng lớn thì phép tính M(x,y) cần nhiều bước hơn nhưng độ chính xác càng cao. Các hằng số π và ln(2) có thể dễ dàng tính nhanh qua các chuỗi hội tụ.

Thuật toán của Feynman

Khi còn ở Phòng thí nghiệm Quốc gia Los Alamos thực hiện Dự án Manhattan, Richard Feynman đã phát triển một thuật toán gần giống với phép chia số lớn. Thuật toán này về sau được sử dụng trên các máy tính song song (Connection Machine). Thuật toán dựa trên cơ sở rằng mọi số thực $1<x<2$ có thể được biểu diễn thành tích của các thừa số khác nhau với dạng $1+2^{-k}$. Thuật toán tuần tự lập tích $P$ đó: nếu $P\cdot (1+2^{-k})<x$ thì nó thay $P$ bằng $P\cdot (1+2^{-k})$, và tăng giá trị $k$ thêm 1 đơn vị bất kể đúng hay sai. Thuật toán dừng lại nếu $k$ đủ lớn để đạt được độ chính xác cần thiết. Vì $\log(x)$ là tổng của các số hạng dạng $\log(1+2^{-k})$ tương ứng với giá trị $k$ sao cho thừa số $1+2^{-k}$ thuộc tích $P$, nên $\log(x)$ có thể được tính bằng phép cộng đơn giản, sử dụng bảng $\log(1+2^{-k})$ với mọi giá trị của $k$, ở bất kỳ cơ số nào.

Ứng dụng

Một con ốc anh vũ thể hiện đường cong logarit xoắn ốc

Logarit có nhiều ứng dụng cả trong lẫn ngoài toán học. Một vài trong số đó có liên quan đến khái niệm về tỷ lệ bất biến. Chẳng hạn, mỗi buồng trong vỏ ốc anh vũ đều gần giống với buồng liền sau, thu nhỏ lại bởi một hằng số tỷ lệ (xoắn ốc logarit). Luật Benford về tần suất xuất hiện chữ số đầu tiên cũng có thể được giải thích qua tỷ lệ bất biến. Logarit cũng có liên hệ với tính chất tự đồng dạng. Chẳng hạn, logarit xuất hiện trong việc nghiên cứu các thuật toán giải phương trình bằng cách chia thành nhiều phương trình con tương tự rồi hợp các tập nghiệm của chúng lại với nhau. Các hình không gian tự đồng dạng cũng đều dựa trên logarit. Thang đo logarit rất cần thiết để định lượng mức độ thay đổi tỉ đối của một đại lượng so với mức độ thay đổi tuyệt đối của nó. Hơn nữa, vì log(x) tăng rất chậm khi x ngày càng lớn nên thang đo logarit được sử dụng để "nén" lại dữ liệu khoa học quy mô lớn. Logarit cũng xuất hiện trong nhiều phương trình khoa học như phương trình tên lửa Tsiolkovsky, phương trình Fenske hay phương trình Fernst.

Thang đo logarit

Bài chi tiết: Thang đo lôgarit

Một biểu đồ logarit thể hiện giá trị của một goldmark tính bằng papiermark trong cuộc siêu lạm phát tại Đức vào những năm 1920

Các đại lượng khoa học thường được biểu diễn theo logarit của các đại lượng khác qua thang đo logarit. Chẳng hạn, decibel là đơn vị đo dựa trên các đại lượng liên quan đến logarit. Nó được dựa trên logarit thập phân của tỷ lệ – 10 lần logarit thập phân của một tỷ lệ công suất hoặc 20 lần logarit thập phân của tỷ lệ hiệu điện thế, và được dùng để định lượng sự hao phí mức điện áp trong truyền tải tín hiệu điện, để miêu tả độ lớn của âm trong âm học, và khả năng hấp thụ bức xạ ánh sáng trong quang học. Tỷ số tín hiệu trên nhiễu mô tả lượng âm không cần thiết so với tín hiệu cũng được đo bằng decibel. Tương tự, tỷ số tín hiệu cực đại trên nhiễu thường được sử dụng để đánh giá chất lượng âm thanh và phương pháp nén ảnh thông qua logarit.

Độ lớn của một trận động đất được đo theo logarit thập phân của năng lượng do động đất sinh ra (thang độ lớn mô men hay thang độ Richter). Chẳng hạn, một trận động đất 5,0 độ giải phóng năng lượng gấp 32 lần (10^1.5) và một trận động đất 6,0 độ giải phóng năng lượng gấp 1000 lần (10³) so với một trận động đất 4,0 độ. Cấp sao biểu kiến là một thang đo logarit thông dụng khác, dùng để đo độ sáng của các ngôi sao qua logarit. Một ví dụ khác nữa là pH trong hóa học; pH là số đối của logarit thập phân của hoạt độ của các ion hydroni (ion hydro trong nước). Hoạt độ của các ion hydroni trong nước cất là 10⁻⁷ mol·l⁻¹, nên pH của nước cất là 7. Giấm thường có pH là khoảng 3, nghĩa là hoạt độ của các ion hydroni trong giấm là khoảng 10⁻³ mol·l⁻¹.

Đồ thị bán logarit (logarit-tuyến tính) ứng dụng logarit theo cách trực quan: một trục (thường là trục tung) được chia tỷ lệ theo logarit. Chẳng hạn, đồ thị ở bên phải thu nhỏ mức tăng từ 1 triệu lên 1 nghìn tỷ xuống cùng độ dài (trên trục tung) so với mức tăng từ 1 lên 1 triệu. Ở những đồ thị như vậy, các hàm mũ dạng f(x) = a · b^x là đường thẳng với hệ số góc bằng với logarit của b. Đồ thị logarit chia tỷ lệ cả hai trục theo logarit, nên hàm mũ dạng f(x) = a · x^k là đường thẳng có hệ số góc bằng với số mũ k. Nó được ứng dụng trong việc nghiên cứu các quy tắc lũy thừa.

Tâm lý học

Logarit xuất hiện trong các luật liên quan đến tri giác con người. Luật Hick nhấn mạnh mối liên hệ logarit giữa thời gian mà một người bỏ ra để chọn một phương án và số lựa chọn mà người đó có. Luật Fitts dự đoán rằng thời gian cần để di chuyển nhanh đến điểm mục tiêu là một hàm logarit của quãng đường và kích thước của mục tiêu. Trong tâm vật lý học, luật Weber–Fechner nhắc đến mối liên hệ logarit giữa kích thích và giác quan, chẳng hạn như khối lượng thực tế so với khối lượng cảm giác của một vật mà một người đang cầm. (Tuy nhiên "luật" này thiếu thực tế so với các mô hình mới hơn, chẳng hạn như luật lũy thừa của Stevens.)

Các nghiên cứu về tâm lý học cho thấy những người được đào tạo ít về toán học thường ước lượng các đại lượng theo logarit, tức là họ đặt một số trên một đường thẳng không được đánh dấu dựa trên logarit của nó sao cho 10 gần với 100 như khi 100 gần với 1000. Khi được đào tạo kỹ càng hơn, họ có xu hướng chuyển sang ước lượng tuyến tính (đặt 1000 xa hơn 10 lần) trong một số trường hợp, trong khi logarit được dùng thay thế khi các số cần đặt quá lớn.

Lý thuyết xác suất và thống kê

Ba hàm mật độ xác suất (PDF) của biến ngẫu nhiên và phân phối loga chuẩn của chúng. Tham số vị trí μ, vốn bằng 0 với cả ba hàm trên, là trung bình của logarit biến ngẫu nhiên, không phải là trung bình của biến đó.

Biểu đồ thể hiện tần suất xuất hiện của chữ số đầu tiên trong dữ liệu dân số của 237 quốc gia trên thế giới. Các chấm đen chỉ phân bố do luật Benford dự đoán.

Logarit nảy sinh trong lý thuyết xác suất: luật số lớn cho rằng, với một đồng xu hai mặt, khi số lần tung tiến đến vô hạn, tỷ lệ xuất hiện mặt ngửa tiệm cận về một nửa. Sự biến động của tỷ lệ này được giải thích qua luật về logarit lặp.

Logarit cũng xuất hiện trong phân phối loga chuẩn. Khi logarit của một biến ngẫu nhiên có một phân phối chuẩn, biến đó được gọi là có một phân phối loga chuẩn. Phân phối loga chuẩn thường gặp trong nhiều lĩnh vực, ở những nơi một biến là tích của nhiều biến dương độc lập ngẫu nhiên, chẳng hạn như nghiên cứu sự nhiễu loạn.

Logarit được dùng trong phép hợp lý cực đại của các mô hình thống kê tham số. Với một mô hình như vậy, hàm hợp lý phụ thuộc vào ít nhất một [[Mô hình tham số|tham số]ưư lấy gần đúng. Giá trị lớn nhất của hàm hợp lý xuất hiện tại tham số có cùng giá trị với giá trị lớn nhất của logarit hàm hợp lý, vì logarit là hàm số tăng. Giá trị của logarit hàm hợp lý là dễ tìm hơn, đặc biệt với các hàm hợp lý được nhân cho biến độc lập ngẫu nhiên.

Luật Benford mô tả sự xuất hiện của các chữ số trong nhiều bộ dữ liệu, chẳng hạn như chiều cao của các tòa nhà. Theo luật này thì xác suất để chữ số đầu tiên của một dữ liệu trong bộ dữ liệu đó là d (từ 1 đến 9) bằng log₁₀(d + 1) − log₁₀(d) bất kể đơn vị đo. Vì vậy, khoảng 30% dữ liệu có thể bắt đầu bằng chữ số 1, khoảng 18% bắt đầu bằng chữ số 2,... Các kiểm toán viên thường đối chiếu dữ liệu với luật Benford để phát hiện các hành vi gian lận trong kế toán.

Độ phức tạp tính toán

Phân tích thuật toán là một nhánh của khoa học máy tính nghiên cứu về hoạt động của thuật toán (chương trình máy tính dùng để giải quyết một vấn đề nhất định). Logarit có vai trò trong việc mô tả các thuật toán chia nhỏ một vấn đề thành nhiều vấn đề con rồi hợp các kết quả lại với nhau.

Chẳng hạn, để tìm một số trong một mảng đã sắp xếp, thuật toán tìm kiếm nhị phân sẽ kiểm tra phần tử đứng giữa mảng và tiếp đến kiểm tra nửa khoảng nằm trước hoặc nằm sau phần tử đứng giữa nếu không tìm thấy số đó. Thuật toán này cần trung bình log₂(N) bước so sánh với N là số phần tử của mảng. Tương tự, thuật toán sắp xếp trộn sắp xếp một mảng bằng cách chia đôi thành hai mảng con và sắp xếp chúng trước khi gộp lại các kết quả. Thuật toán sắp xếp trộn thường tốn một khoảng thời gian xấp xỉ tỷ lệ thuận với N · log(N). Cơ số của logarit không được nhắc đến cụ thể, vì kết quả chỉ thay đổi theo một hằng số nhất định khi dùng cơ số khác. Người ta không quan tâm đến hằng số đó khi phân tích thuật toán dưới mô hình chi phí thống nhất.

Một hàm số f(x) được gọi là hàm số tăng logarit nếu f(x) tỷ lệ thuận với logarit của x. (Tuy nhiên, một số tài liệu sinh học sử dụng thuật ngữ này đối với hàm mũ khi viết về sự sinh trưởng của sinh vật.) Chẳng hạn, mọi số tự nhiên N đều có thể được biểu diễn dưới dạng nhị phân sử dụng không quá log₂(N) + 1 bit. Nói cách khác, lượng bộ nhớ cần dùng để lưu trữ N tăng theo logarit của N.

Entropy và sự hỗn loạn

Một mô hình bàn bida. Hai hạt, bắt đầu từ tâm với góc sai khác nhau 1 độ, bắt đầu phân ra di chuyển hỗn loạn do phản xạ trên thành bàn.

Entropy là một phép đo về sự hỗn loạn của một hệ. Trong cơ học thống kê, entropy S của một hệ vật lý được xác định là

$S=-k\sum _{i}p_{i}\ln(p_{i}).\,$

Tổng này là trên tất cả trạng thái i của hệ được xét, chẳng hạn như vị trí của các phân tử khí trong bình chứa. Hơn nữa, p_i là xác suất để hệ đạt được trạng thái i và k là hằng số Boltzmann. Tương tự, entropy thông tin mô tả mức độ hỗn loạn của thông tin. Nếu người nhận một thông điệp kỳ vọng nhận được bất kỳ trong số N thông điệp có thể với xác suất giống nhau thì lượng thông tin truyền tải bởi một thông điệp như vậy được định lượng là log₂(N) bit.

Phép lũy thừa Lyapunov sử dụng logarit để đo mức độ hỗn loạn của một hệ thống động lực. Chẳng hạn, khi một hạt di chuyển trên một bàn bida, chỉ một thay đổi rất nhỏ về góc cũng có thể làm thay đổi hoàn toàn hướng đi của hạt đó. Hệ thống như vậy hỗn loạn một cách tất định, vì những sai sót nhỏ ở điều kiện ban đầu thường dẫn đến những kết quả khác hẳn nhau.

Phân dạng

Tam giác Sierpinski (bên phải) được tạo nên bằng cách lặp đi lặp lại thay một tam giác đều bằng ba tam giác đều nhỏ hơn.

Logarit xuất hiện trong định nghĩa về số chiều phân dạng. Phân dạng là một vật thể hình học có cấu trúc tự đồng dạng: mỗi hình nhỏ hơn đều trông giống như hình tổng thể. Tam giác Sierpinski được tạo ra từ ba bản sao của chính nó, mỗi hình có chiều dài bằng một nửa hình ban đầu. Theo đó, số chiều Hausdorff của cấu trúc này là ln(3)/ln(2) ≈ 1,58. Một khái niệm khác về số chiều dựa trên logarit được suy ra bởi việc đếm số hình vuông đơn vị để bao phủ hết bề mặt phân dạng được xét.

Âm nhạc

Bốn quãng tám khác nhau trên thang đo tuyến tính và thang đo logarit (khi tai nghe thấy chúng).

Logarit có liên hệ đến cung và quãng trong âm nhạc. Trong hệ thống âm tự nhiên, tỷ lệ tần số chỉ phụ thuộc vào quãng giữa hai tông nhạc, không phụ thuộc vào tần số hay cao độ của từng tông cụ thể. Chẳng hạn, nốt A có tần số là 440 Hz và nốt B♭ có tần số là 466 Hz. Quãng giữa nốt A và nốt B♭ là nửa cung, giống như quãng giữa nốt B♭ và nốt B (tần số 493 Hz), vì tỷ lệ tần số của hai quãng trên gần bằng nhau:

${\frac {466}{440}}\approx {\frac {493}{466}}\approx 1,059\approx {\sqrt[{12}]{2}}.$

Do đó, logarit có thể được dùng để miêu tả các quãng: một quãng được đo theo đơn vị nửa cung bằng cách lấy logarit cơ số 2^1/12 của tỷ lệ tần số, trong khi logarit cơ số 2^1/1200 của nó đo quãng đó theo cent, bằng một phần trăm so với nửa cung.

Quãng (phát hai tông cùng lúc)	Tông 1/12 phátⓘ	Nửa cung phátⓘ	Quãng 5/4 phátⓘ	Quãng 3 trưởng phátⓘ	Quãng 3 cung phátⓘ	Quãng tám phátⓘ
Tỷ lệ tần số r	$2^{\frac {1}{72}}\approx 1,0097$	$2^{\frac {1}{12}}\approx 1,0595$	${\tfrac {5}{4}}=1,25$	${\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1,2599\end{aligned}}$	${\begin{aligned}2^{\frac {6}{12}}&={\sqrt {2}}\\&\approx 1,4142\end{aligned}}$	$2^{\frac {12}{12}}=2$
Số nửa cung tương ứng $\log _{\sqrt[{12}]{2}}(r)=12\log _{2}(r)$	${\tfrac {1}{6}}\,$	$1\,$	$\approx 3,8631\,$	$4\,$	$6\,$	$12\,$
Số cent tương ứng $\log _{\sqrt[{1200}]{2}}(r)=1200\log _{2}(r)$	$16{\tfrac {2}{3}}\,$	$100\,$	$\approx 386,31\,$	$400\,$	$600\,$	$1200\,$

Lý thuyết số

Logarit tự nhiên có liên hệ gần với việc đếm số nguyên tố (2, 3, 5, 7, 11, ...), một chủ đề quan trọng trong lý thuyết số. Với mỗi số nguyên x, số lượng số nguyên tố nhỏ hơn hoặc bằng x được ký hiệu là π(x). Theo định lý số nguyên tố, giá trị gần đúng của π(x) được cho bởi

${\frac {x}{\ln(x)}},$

vì giới hạn của tỷ số giữa π(x) và x/ln(x) bằng 1 khi x dần đến vô hạn. Do đó, khi chọn một số ngẫu nhiên nằm giữa 1 và x thì xác suất để số đó là số nguyên tố tỷ lệ nghịch với số chữ số của x. Một xấp xỉ chính xác hơn nữa của π(x) được cho bởi hàm tích phân logarit bù Li(x):

$\mathrm {Li} (x)=\int _{2}^{x}{\frac {1}{\ln(t)}}\,dt.$

Giả thuyết Riemann, một trong những phỏng đoán toán học mở lâu đời nhất, có thể được phát biểu trên cơ sở so sánh π(x) và Li(x). Định lý Erdős–Kac mô tả số các thừa số nguyên tố khác nhau cũng liên quan đến logarit tự nhiên.

Logarit của n giai thừa, n! = 1 · 2 · ... · n, được cho bởi

$\ln(n!)=\ln(1)+\ln(2)+\cdots +\ln(n).\,$

Biểu thức này được dùng để suy ra phép xấp xỉ Stirling, một phép tính gần đúng n! với n lớn.

Khái quát hóa

Logarit phức

Bài chi tiết: Logarit phức

Một điểm z = x + iy trong mặt phẳng phức. Cả hai góc φ và φ' đều là argumen của z.

Mọi nghiệm phức a của phương trình

$e^{a}=z$

được gọi là logarit phức của z, với z là một số phức. Mỗi số phức thường có dạng z = x + iy với x và y là số thực và i là đơn vị ảo (căn bậc hai của −1). Một số như vậy có thể được biểu diễn bằng một điểm trong mặt phẳng phức như hình bên phải. Mặt phẳng phức thường biểu thị một số phức z khác không theo giá trị tuyệt đối của nó, tức là khoảng cách r đến điểm gốc, và một góc hợp bởi trục hoành thực Re và đường thẳng đi qua gốc tọa độ và z. Góc này được gọi là argumen của z.

Giá trị tuyệt đối r của z được tính bằng

$\textstyle r={\sqrt {x^{2}+y^{2}}}.$

Áp dụng biểu diễn hình học của $\sin$ và $\cos$ và tính tuần hoàn của chúng với chu kỳ $2\pi$, mỗi số phức z cũng có thể được biểu diễn dưới dạng

$z=x+iy=r(\cos \varphi +i\sin \varphi )=r(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )),$

với k là số nguyên. Rõ ràng argumen của z không phải là duy nhất: cả φ và φ' = φ + 2kπ đều là argumen của z với mọi số nguyên k, vì thêm 2kπ radian hoặc k⋅360° vào φ tức là "quay" góc φ quanh gốc tọa độ k vòng. Số phức cuối cùng luôn là z, như được minh họa trong hình bên phải với k = 1. Ta có thể chọn đúng một trong số các argumen của z làm argumen chính, ký hiệu là Arg(z) với chữ cái A in hoa, bằng cách giới hạn φ xuống một vòng quay nhất định, chẳng hạn như $-\pi <\varphi \leq \pi$ hoặc $0\leq \varphi <2\pi .$ Các nửa khoảng này được gọi là ''nhánh chính'' của hàm argumen.

Miền tô màu của logarit phức Log(z). Điểm màu đen tại z = 1 tương ứng với giá trị tuyệt đối bằng không và màu sáng hơn, sẫm hơn biểu thị giá trị tuyệt đối lớn hơn. Sắc độ của màu chỉ argumen của Log(z).

Công thức Euler liên hệ các hàm lượng giác sin và cosin với hàm số mũ phức:

$e^{i\varphi }=\cos \varphi +i\sin \varphi .$

Áp dụng công thức trên và tính chất tuần hoàn, ta có:

${\begin{array}{lll}z&=&r\left(\cos \varphi +i\sin \varphi \right)\\&=&r\left(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )\right)\\&=&re^{i(\varphi +2k\pi )}\\&=&e^{\ln(r)}e^{i(\varphi +2k\pi )}\\&=&e^{\ln(r)+i(\varphi +2k\pi )}=e^{a_{k}},\end{array}}$

với ln(r) là logarit tự nhiên thực duy nhất, a_k là logarit phức của z và k là một số nguyên bất kỳ. Do đó, logarit phức của z, bao gồm tất cả các số phức a_k sao cho lũy thừa bậc a_k của e bằng z, là một tập hợp vô số các giá trị a_k thỏa mãn

$a_{k}=\ln(r)+i(\varphi +2k\pi ),\quad$ với k là một số nguyên.

Đặt k sao cho $\varphi +2k\pi$ nằm trong các nửa khoảng được xác định như trên thì a_k được gọi là giá trị chính của logarit phức, ký hiệu là Log(z) với chữ cái L in hoa. Argumen chính của mọi số thực dương x bằng 0; do đó Log(x) là một số thực bằng với logarit tự nhiên thực. Tuy vậy, các công thức về logarit của một tích hay lũy thừa không áp dụng được cho giá trị chính của logarit phức.

Hình bên phải miêu tả miền tô màu của Log(z), trong đó z được giới hạn về nửa khoảng (-π, π]. Có thể thấy nhánh tương ứng của logarit phức bị đứt đoạn trên toàn bộ phần âm của trục hoành thực, tại đó sắc độ thay đổi bất chợt. Sự đứt đoạn này nảy sinh từ việc chuyển sang phân vùng khác trong cùng một nhánh khi đi qua một đường biên (không chuyển qua giá trị k tương ứng của nhánh lân cận). Một quỹ tích như vậy được gọi là nhánh cắt. Nếu bỏ qua điều kiện của argumen thì "argumen của z" và "logarit của z" đều trở thành hàm đa trị.

Hàm ngược của các hàm mũ khác

Lũy thừa xuất hiện trong nhiều lĩnh vực của toán học và hàm ngược của nó thường được gọi là logarit. Chẳng hạn, logarit của một ma trận là hàm ngược (đa trị) của hàm mũ ma trận. Một ví dụ khác là hàm logarit p-adic, hàm ngược của hàm mũ p-adic. Cả hai đều được xác định qua chuỗi Taylor tương tự như với số thực. Trong hình học vi phân, ánh xạ mũ ánh xạ không gian tiếp tuyến tại một điểm của một đa tạp đến một lân cận của điểm đó, và ánh xạ ngược lại với nó được gọi là ánh xạ logarit.

Trong nhóm hữu hạn, lũy thừa là nhân lặp đi lặp lại một phần tử b trong nhóm với chính nó. Logarit rời rạc là nghiệm nguyên n của phương trình

$b^{n}=x,\,$

với x là một phần tử trong nhóm. Phép lũy thừa rời rạc có thể dễ dàng thực hiện được, nhưng logarit rời rạc được cho là khó tính được trong một số nhóm. Tính bất đối xứng này có những ứng dụng quan trọng trong mật mã hóa khóa công khai, chẳng hạn như trong trao đổi khóa Diffie–Hellman, một phương pháp cho phép trao đổi khóa mật mã một cách bảo mật trên các kênh thông tin không an toàn. Logarit Zech có liên hệ với logarit rời rạc đối với nhóm nhân của các phần tử khác không trong một trường hữu hạn.

Các hàm ngược khác liên quan đến logarit bao gòm logarit nhân đôi ln(ln(x)), siêu logarit (có dạng gần giống với logarit lặp trong khoa học máy tính), hàm Lambert W và logit. Chúng lần lượt là hàm ngược của hàm lũy thừa nhân đôi, túc thừa, f(w) = we^w, và hàm logistic.

Các khái niệm liên quan

Trong lý thuyết nhóm, đồng nhất thức log(cd) = log(c) + log(d) biểu thị một đẳng cấu nhóm giữa các số thực dưới phép nhân và các số thực dưới phép cộng. Hàm logarit là đẳng cấu liên tục duy nhất giữa các nhóm này. Bằng đẳng cấu đó, độ đo Haar (độ đo Lebesgue) dx trên các số thực tương ứng với độ đo Haar dx/x trên các số thực dương. Các số thực không âm có cả phép nhân và phép cộng và hợp lại thành một bán vành gọi là bán vành xác suất; đó cũng là một bán trường. Logarit sau đó chuyển phép nhân thành phép cộng (công thức tích) và chuyển phép cộng thành phép cộng log (LogSumExp) dựa trên phép đẳng cấu giữa bán vành xác suất và bán vành log.

Logarit 1-dạng df/f xuất hiện trong giải tích phức và hình học đại số, là một dạng vi phân với cực điểm logarit.

Hàm đa loga là hàm số xác định bởi

$\operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}}.$

Nó có liên hệ với logarit tự nhiên: Li₁(z) = −ln(1 − z). Hơn nữa, Li_s(1) bằng với hàm zeta Riemann ζ(s).

Xem thêm

• Căn bậc n
• Lũy thừa
• Giới hạn
• Tích phân

Liên kết ngoài

• Tư liệu liên quan tới Logarithm tại Wikimedia Commons
• Định nghĩa của logarit tại Wiktionary
• Khan Academy: Logarithms, free online micro lectures
• Hazewinkel, Michiel biên tập (2001), “Logarithmic function”, Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4
• Edward Wright, Translation of Napier's work on logarithms, Bản gốc lưu trữ ngày 3 tháng 12 năm 2002
• Glaisher, James Whitbread Lee (1911). “Logarithm” . Trong Chisholm, Hugh (biên tập). Encyclopædia Britannica. 16 (ấn bản 11). Cambridge University Press. tr. 868–77.