Thuyết tương đối rộng
Thuyết tương đối rộng hay thuyết tương đối tổng quát (tiếng Anh: general relativity) là lý thuyết hình học của lực hấp dẫn do nhà vật lý Albert Einstein công bố vào năm 1915[2] và hiện tại được coi là lý thuyết miêu tả hấp dẫn thành công của vật lý hiện đại. Thuyết tương đối tổng quát thống nhất thuyết tương đối hẹp và định luật vạn vật hấp dẫn của Newton, đồng thời nó miêu tả lực hấp dẫn (trường hấp dẫn) như là một tính chất hình học của không gian và thời gian, hoặc không thời gian. Đặc biệt, độ cong của không thời gian có liên hệ chặt chẽ trực tiếp với năng lượng và động lượng của vật chất và bức xạ. Liên hệ này được xác định bằng phương trình trường Einstein, một hệ phương trình đạo hàm riêng phi tuyến.
Nhiều tiên đoán và hệ quả của thuyết tương đối rộng khác biệt hẳn so với kết quả của vật lý cổ điển, đặc biệt khi đề cập đến sự trôi đi của thời gian, hình học của không gian, chuyển động của vật thể khi rơi tự do và sự lan truyền của ánh sáng. Những sự khác biệt như vậy bao gồm sự giãn thời gian do hấp dẫn, thấu kính hấp dẫn, dịch chuyển đỏ do hấp dẫn của ánh sáng, và sự trễ thời gian do hấp dẫn. Mọi quan sát và thí nghiệm đều xác nhận các hiệu ứng này cho tới nay. Mặc dù có một số lý thuyết khác về lực hấp dẫn cũng được nêu ra, nhưng lý thuyết tương đối tổng quát là một lý thuyết đơn giản nhất phù hợp các dữ liệu thực nghiệm. Tuy thế, vẫn còn tồn tại những câu hỏi mở, căn bản nhất như các nhà vật lý chưa biết làm thế nào kết hợp thuyết tương đối rộng với các định luật của vật lý lượng tử nhằm tạo ra một lý thuyết đầy đủ và nhất quán là thuyết hấp dẫn lượng tử.
Lý thuyết của Einstein có nhiều ứng dụng quan trọng trong vật lý thiên văn. Nó chỉ ra trực tiếp sự tồn tại của lỗ đen – những vùng của không thời gian trong đó không gian và thời gian bị uốn cong đến mức ngay cả ánh sáng cũng không thể thoát ra được – một trạng thái cuối cùng của các ngôi sao khối lượng lớn. Có rất nhiều nguồn bức xạ mạnh phát ra từ một vài loại thiên thể cố định dựa trên sự tồn tại của lỗ đen; ví dụ, các microquasar và nhân các thiên hà hoạt động thể hiện sự có mặt của tương ứng lỗ đen khối lượng sao và lỗ đen có khối lượng khổng lồ. Sự lệch của tia sáng do trường hấp dẫn làm xuất hiện hiệu ứng thấu kính hấp dẫn, trong đó nhiều hình ảnh của cùng một thiên hà hiện lên qua ảnh chụp. Thuyết tương đối tổng quát miêu tả các tính chất của sóng hấp dẫn mà đã được xác nhận một cách trực tiếp bởi nhóm Advanced LIGO. Hơn nữa, thuyết tương đối rộng còn là cơ sở cho các mô hình vũ trụ học hiện tại về sự đang giãn nở không ngừng của vũ trụ.
| Thuyết tương đối rộng |
|---|
 |
|
Dẫn nhập · Lịch sử · Nguyên lý toán học Kiểm chứng |
|
Khái niệm cơ sở |
|
Hiệu ứng và hệ quả |
|
Lý thuyết phát triển |
|
Nhà vật lý Einstein · Lorentz · Hilbert · Poincare · Schwarzschild · Sitter · Reissner · Nordström · Weyl · Eddington · Friedman · Milne · Zwicky · Lemaître · Gödel · Wheeler · Robertson · Bardeen · Walker · Kerr · Chandrasekhar · Ehlers · Penrose · Hawking · Taylor · Hulse · Stockum · Taub · Newman · Khâu Thành Đồng · Thorne khác |
| Thuyết tương đối hẹp |
|---|
 |
Lịch sử[sửa | sửa mã nguồn]

Ngay sau khi phát triển thuyết tương đối đặc biệt năm 1905, Einstein bắt đầu suy nghĩ về sự mâu thuẫn giữa lực hấp dẫn Newton với lý thuyết này. Năm 1907, ông nhận ra sự liên hệ (hay tương đương cục bộ) giữa lực hấp dẫn và hệ quy chiếu gia tốc (ông coi đây là ý tưởng hạnh phúc nhất của đời mình) và nêu ra một thí nghiệm suy tưởng đơn giản trong đó có một người quan sát trong thang máy rơi tự do. Ông đã phải mất tám năm theo đuổi nhằm tìm kiếm lý thuyết hấp dẫn tương đối tính. Sau nhiều nhầm lẫn và đi lệch hướng, cuối cùng ông đã tìm ra được phương trình hấp dẫn và miêu tả nó trong cuộc họp của Viện hàn lâm Khoa học Phổ vào tháng 11 năm 1915 mà ngày nay gọi là phương trình trường Einstein. Hệ phương trình này cho biết hình học của không thời gian bị ảnh hưởng bởi sự có mặt của vật chất như thế nào, và lực hấp dẫn do sự cong của hình học không thời gian. Phương trình trường Einstein là mảnh ghép trung tâm của thuyết tương đối tổng quát.[3]
Phương trình trường Einstein là hệ phương trình vi phân riêng phần phi tuyến và rất khó để giải. Einstein đã sử dụng phương pháp xấp xỉ nhằm suy luận những hệ quả đầu tiên của lý thuyết. Nhưng ngay đầu năm 1916, nhà thiên văn vật lý Karl Schwarzschild tìm ra nghiệm chính xác không tầm thường đầu tiên của phương trình trường Einstein mà ngày nay gọi là mêtric Schwarzschild. Nghiệm này là cơ sở lý thuyết cho mô hình vật lý về trạng thái cuối cùng của suy sụp hấp dẫn, dẫn đến sự hình thành của một số thiên thể trong đó có lỗ đen dạng đối xứng cầu. Trong cùng năm, nghiệm Schwarzschild đã được tổng quát thành nghiệm chính xác cho vật thể có điện tích, hay chính là mêtric Reissner–Nordström, nghiệm này mô tả lỗ đen tích điện không quay.[4] Năm 1917, Einstein áp dụng lý thuyết của ông cho toàn bộ vũ trụ, khai sinh ra ngành vũ trụ học tương đối tính.[5] Theo tư tưởng đương thời, ông đã giả định vũ trụ tĩnh tại vĩnh hằng, và phải cộng thêm một tham số mới vào trong phương trình trường ban đầu của mình—hằng số vũ trụ học—nhằm thu được kết quả như "quan sát" từ bấy lâu nay.[6] Tuy thế, năm 1929, những nghiên cứu của nhà thiên văn Edwin Hubble và những người khác lại chỉ ra vũ trụ đang giãn nở. Và kết quả quan sát này lại phù hợp với nghiệm mô tả vũ trụ đang giãn nở do nhà vật lý người Nga Alexander Friedman tìm ra từ năm 1922 mà không đòi hỏi có hằng số vũ trụ học. Linh mục và nhà vũ trụ học người Bỉ Georges Lemaître đã sử dụng nghiệm này nhằm miêu tả kịch bản sơ khai của mô hình Vụ Nổ Lớn, mô hình nói rằng vũ trụ ban đầu đã tiến hóa từ trạng thái cực kỳ nóng và đậm đặc.[7] Sau này, Einstein coi hằng số vũ trụ học là sai lầm lớn nhất của đời ông.[8]
Trong suốt thời kì từ thập niên 1920 đến thập niên 1950, các nhà vật lý vẫn coi thuyết tương đối tổng quát một lý thuyết kỳ lạ trong các lý thuyết vật lý. Nó đẹp hơn lý thuyết của Newton, phù hợp với thuyết tương đối hẹp và giải thích được một vài hiệu ứng mà lý thuyết Newton chưa thành công. Chính Einstein đã chỉ ra vào năm 1915 rằng lý thuyết của ông đã giải thích được chuyển động dị thường của điểm cận nhật của Sao Thủy mà không cần tới bất kì một tham số nào.[9] Vào năm 1919 một đoàn thám hiểm dẫn đầu bởi Arthur Eddington đã xác nhận tiên đoán của thuyết tương đối tổng quát về sự lệch ánh sáng khi nó đi gần Mặt trời bằng cách theo dõi nhật thực vào tháng 5,[10] khiến Einstein ngay lập tức trở nên nổi tiếng.[11] Và lý thuyết trở thành hướng đi chính của vật lý lý thuyết và thiên văn vật lý trong giai đoạn phát triển từ 1960 đến 1975, hay thời kỳ vàng của thuyết tương đối rộng.[12] Các nhà vật lý bắt đầu nắm bắt được khái niệm lỗ đen, và đồng nhất những đối tượng thiên văn vật lý này với quasar trong thiên văn quan sát.[13] Có thêm nhiều kiểm nghiệm chính xác trong hệ Mặt Trời đã chứng tỏ sức mạnh tiên đoán của lý thuyết,[14] và trong vũ trụ học tương đối tính cũng vậy với rất nhiều quan sát đo lường nhằm kiểm chứng hệ quả của lý thuyết.[15]
Từ cơ học cổ điển đến thuyết tương đối rộng[sửa | sửa mã nguồn]
Chúng ta có thể hiểu thuyết tương đối rộng thông qua những điểm tương tự và khác biệt của nó so với lý thuyết Newton. Bước đầu tiên là chỉ ra cơ học cổ điển và định luật vạn vật hấp dẫn cho phép miêu tả theo ngôn ngữ hình học. Bằng cách kết hợp miêu tả này với định luật của thuyết tương đối hẹp sẽ cho chúng ta khám phá thuyết tương đối rộng một cách tự nhiên.[16]
Mô tả bằng hình học của lực hấp dẫn Newton[sửa | sửa mã nguồn]


Cơ sở của vật lý cổ điển là khái niệm chuyển động của một vật thể, kết hợp giữa chuyển động tự do (hay quán tính) và chuyển động khi có ngoại lực tác dụng. Các chuyển động này được miêu tả bằng phương trình trong không gian 3 chiều Euclid và sử dụng khái niệm thời gian tuyệt đối. Những ngoại lực tác dụng lên vật thể làm quỹ đạo vật lệch khỏi quỹ đạo của chuyển động quán tính tuân theo định luật thứ hai của Newton về chuyển động, phát biểu là tổng lực tác dụng lên vật bằng khối lượng (quán tính) nhân với gia tốc của nó.[17] Tiếp theo, chuyển động quán tính được liên hệ với hình học của không gian và thời gian: trong hệ quy chiếu quán tính của cơ học cổ điển, các vật chuyển động tự do với vận tốc không đổi sẽ có quỹ đạo là đường thẳng. Theo ngôn ngữ của vật lý hiện đại, quỹ đạo của chúng là đường trắc địa, những tuyến thế giới thẳng (world lines, hay đường thế giới) trong không thời gian cong và đường trắc địa chính là đường thẳng trong hình học phẳng.[18]
Ngược lại, chúng ta mong muốn rằng nhờ áp dụng chuyển động quán tính - một khi biết được chuyển động thực của vật thể do ảnh hưởng của ngoại lực nào (như lực điện từ hoặc ma sát) - để xác định ra hình học của không gian, cũng như tọa độ thời gian. Tuy nhiên, có một sự khó khăn khi xuất hiện hấp dẫn. Theo định luật vạn vật hấp dẫn Newton, và những thí nghiệm độc lập của Eötvös và các thí nghiệm sau đó (xem thí nghiệm Eötvös), vật rơi tự do (còn gọi là nguyên lý tương đương yếu, hay sự bằng nhau giữa khối lượng quán tính và khối lượng hấp dẫn thụ động): quỹ đạo của vật thử khi rơi tự do chỉ phụ thuộc vào vị trí và vận tốc ban đầu của nó, chứ không phụ thuộc vào nó cấu tạo bằng vật chất gì (như lực điện từ còn phụ thuộc vào điện tích hạt thử).[19] Có một minh họa đơn giản điều này thể hiện trong thí nghiệm tưởng tượng của Einstein, ở hình bên cạnh: đối với một quan sát viên trong thang máy kín, anh ta không thể biết được, bằng theo dõi quỹ đạo của các vật như quả bóng rơi, rằng anh ta đang ở trong căn phòng đứng yên trên mặt đất và trong một trường hấp dẫn, hay đang ở trong tàu vũ trụ chuyển động tự do trong không gian với gia tốc bằng gia tốc hấp dẫn.[20]
Nếu chỉ dựa vào sự rơi tự do của vật, chúng ta không thể phân biệt được chỉ bằng quan sát giữa chuyển động quán tính và chuyển động chịu ảnh hưởng của lực hấp dẫn. Sự không phân biệt được này gợi ra một định nghĩa mới cho chuyển động quán tính: chuyển động của vật rơi tự do trong trường hấp dẫn. Định nghĩa mới về chuyển động quán tính này cũng cho phép xác định ra hình học của không gian và thời gian theo ngôn ngữ toán học, quỹ đạo của vật chính là chuyển động trên đường trắc địa. Trong phương trình đường trắc địa chứa hệ số liên thông phụ thuộc vào gradien của thế năng hấp dẫn. Không gian của cơ học Newton theo cách xây dựng này vẫn thuần túy là hình học Euclid phẳng. Hình học này tác động đến chuyển động của vật chất nhưng không bị ảnh hưởng bởi vật chất và tồn tại một cách tuyệt đối. Tuy nhiên toàn bộ không thời gian vật lý lại là một cấu trúc phức tạp. Như được chỉ ra bằng các thí nghiệm tưởng tượng đơn giản về quỹ đạo rơi tự do của các hạt thử khác nhau, khi dịch chuyển các vectơ không thời gian - ký hiệu cho vận tốc của hạt (các vectơ kiểu thời gian, có 4 thành phần tọa độ) - sẽ cho kết quả là các vectơ khác nhau dọc theo quỹ đạo của hạt; hay nói về mặt toán học, liên thông Newton không khả tích được (các vectơ vận tốc khi dịch chuyển trên quỹ đạo sẽ không còn song song với vectơ ban đầu nữa). Từ điều này, chúng ta có thể kết luận rằng không thời gian là cong. Mô hình hình học phẳng của hấp dẫn Newton chỉ sử dụng các khái niệm hiệp biến, có nghĩa là nó công nhận một hệ quy chiếu quán tính toàn cục và mô tả hiện tượng hấp dẫn đúng trong mọi hệ tọa độ.[21] Theo cách miêu tả hình học này, các hiệu ứng thủy triều — gia tốc tương đối giữa các vật thể gần nhau khi rơi tự do — được liên hệ với đạo hàm của liên thông, chỉ ra hình học thay đổi như thế nào bởi sự có mặt khối lượng.[22]
Chuyển sang tương đối tính[sửa | sửa mã nguồn]

Nếu mô hình lực hấp dẫn Newton có thể biểu diễn bằng hình học thì cơ sở vật lý của nó, cơ học cổ điển, chỉ là trường hợp giới hạn của cơ học tương đối tính (đặc biệt) đối với chuyển động có vận tốc nhỏ.[23] Theo ngôn ngữ của đối xứng: khi bỏ qua ảnh hưởng của trường hấp dẫn, các phương trình vật lý tuân theo bất biến Lorentz giống như của thuyết tương đối hẹp hơn là tuân theo bất biến Galileo như trong cơ học cổ điển. (Nhóm đối xứng của thuyết tương đối hẹp là nhóm Poincaré bao gồm cả phép tịnh tiến và phép quay.) Sự khác nhau giữa cơ học cổ điển và thuyết tương đối hẹp trở lên rõ rệt khi các vật có vận tốc gần với tốc độ ánh sáng, và khi xét đến những quá trình năng lượng cao.[24]
Với đối xứng Lorentz, chúng ta có thêm những cấu trúc mới. Chúng được xác định bằng tập hợp nón ánh sáng (xem hình bên trái). Các nón ánh sáng cho phép định nghĩa cấu trúc nhân quả: đối với mỗi sự kiện A, về nguyên lý có một tập các sự kiện, hoặc ảnh hưởng đến A hoặc bị ảnh hưởng bởi A thông qua tín hiệu hoặc tương tác mà không vượt quá tốc độ ánh sáng (như sự kiện B trong hình), và một tập các sự kiện không thể liên quan được đến A (như sự kiện C trong hình). Tập này gọi là tập những quan sát viên độc lập.[25] Khi gắn với tuyến thế giới (world-lines) của hạt rơi tự do, chúng ta sử dụng nón ánh sáng nhằm khôi phục lại mêtric nửa-Riemannian của không thời gian, ít nhất đối với số hạng vô hướng dương. Theo thuật ngữ toán học, quá trình này xác định lên cấu trúc bảo giác.[26]
Thuyết tương đối hẹp không miêu tả lực hấp dẫn, do vậy các nhà vật lý áp dụng nó cho những mô hình không tính đến lực hấp dẫn. Bởi vì mô hình hấp dẫn Newton nói rằng lực hấp dẫn giữa hai vật thể tác dụng một cách tức thì, không kể chúng ở cách xa bao nhiêu (hay tồn tại những hệ quy chiếu quán tính toàn cục), do vậy lý thuyết Newton vi phạm bất biến Lorentz. Khi tính đến trường hấp dẫn, bằng áp dụng sự rơi tự do, cách lý giải tương tự như phần trước được áp dụng: không có một hệ quy chiếu quán tính toàn cục tồn tại trong lý thuyết tương đối tổng quát. Thay vì vậy chúng ta chỉ có thể sử dụng những hệ quy chiếu quán tính cục bộ "xấp xỉ" di chuyển dọc theo quỹ đao hạt rơi tự do. Chuyển thành ngôn ngữ của không thời gian: những tuyến thế giới thẳng kiểu thời gian mà xác định hệ quy chiếu quán tính không có trường hấp dẫn sẽ bị lệch thành những đường cong tương đối với nhau trong trường hấp dẫn (Giống như khi thả hai quả bóng rơi tự do, tưởng như chúng rơi song song với nhau nhưng thực tế quỹ đạo của chúng gặp nhau tại tâm Trái Đất, hay quỹ đạo hai quả bóng bị lệch tương đối với nhau khi có mặt trường hấp dẫn.) và điều này gợi ra rằng trường hấp dẫn làm thay đổi hình học của không thời gian từ phẳng sang cong.[27]
Nhưng có một câu hỏi xuất hiện trước tiên là liệu hệ quy chiếu cục bộ mới gắn liền với vật rơi tự do có giống với hệ quy chiếu mà trong đó các định luật của thuyết tương đối hẹp thỏa mãn — lý thuyết dựa trên cơ sở sự không đổi của tốc độ ánh sáng trong chân không, và cũng mô tả lý thuyết điện từ học cổ điển. Bằng sử dụng những hệ quy chiếu tương đối tính của thuyết tương đối hẹp (như hệ quy chiếu gắn liền với mặt đất-phòng thí nghiệm, hay hệ quy chiếu rơi tự do), chúng ta có thể dẫn ra những kết quả khác nhau cho hiệu ứng dịch chuyển đỏ do hấp dẫn, hiệu ứng dịch chuyển tần số của ánh sáng khi nó truyền qua trường hấp dẫn (xem bên dưới). Những đo đạc thử nghiệm chỉ ra rằng ánh sáng lan truyền trong các hệ quy chiếu rơi tự do có quỹ đạo và tần số giống với khi ánh sáng lan truyền trong những hệ quy chiếu quán tính của thuyết tương đối hẹp. Và ánh sáng lan truyền trong trường hấp dẫn có quỹ đạo và sự dịch chuyển tần số giống như khi nó lan truyền trong hệ quy chiếu đang gia tốc với gia tốc bằng gia tốc hấp dẫn.[28] Tổng quát hóa phát biểu này tương ứng với phát biểu "các định luật của thuyết tương đối hẹp thỏa mãn một cách xấp xỉ tốt trong những hệ quy chiếu rơi tự do (và không quay)", còn gọi là nguyên lý tương đương Einstein, một nguyên lý nền tảng của thuyết tương đối tổng quát.[29]
Các thí nghiệm cũng chỉ ra rằng thời gian đo bởi những đồng hồ trong trường hấp dẫn — thời gian riêng, thuật ngữ của vật lý học — không tuân theo các định luật của thuyết tương đối hẹp (hàm ý thời gian bị cong). Trong ngôn ngữ của hình học không thời gian, nó không được đo bằng mêtric Minkowski. Như trong trường hợp lực hấp dẫn Newton, điều này gợi ra lý thuyết tương đối rộng cần một hình học tổng quát để miêu tả. Ở quy mô nhỏ, mọi hệ quy chiếu rơi tự do đều tương đương với nhau và miêu tả xấp xỉ bằng mêtric Minkowski. Hệ quả là, chúng ta sẽ cần phải tổng quát hình học Minkowski thành hình học các không gian cong. Tenxơ mêtric xác định lên cấu trúc hình học — đặc biệt nó cho phép đo độ dài và góc — khác với mêtric Minkowski của thuyết tương đối hẹp, nó là mêtric tổng quát của mêtric đa tạp giả-Riemann. Hơn nữa, mỗi mêtric Riemann được kết hợp một cách tự nhiên với một loại liên thông đặc biệt, liên thông Levi-Civita, và thực tế liên thông này thỏa mãn nguyên lý tương đương và làm cho không thời gian của thuyết tương đối tổng quát trên phương diện cục bộ giống với không thời gian Minkowski (có nghĩa là khi chọn hệ tọa độ quán tính cục bộ phù hợp, tenxơ mêtric của thuyết tương đối rộng trở thành tenxơ mêtric Minkowski, cũng như đạo hàm riêng bậc nhất và các hệ số liên thông triệt tiêu - tương đương với không có trường hấp dẫn ở hệ toạ độ cục bộ này). Tenxơ mêtric thể hiện tính động lực của hình học không thời gian, nó cho thấy vật chất ảnh hưởng lên hình học như thế nào cũng như sự xuất hiện của nó trong phương trình chuyển động của hạt thử.[30]
- Trong không thời gian Minkowski phẳng, với hệ tọa độ một trong những bất biến Lorentz là "khoảng không thời gian" giữa hai sự kiện
- Nếu thì hai sự kiện nằm trên tuyến thế giới (world line) kiểu thời gian (time-like), và mọi sự kiện thực có liên hệ nhân quả với nhau-một sự kiện nằm trong nón ánh sáng của sự kiện kia-sẽ nằm trên đường kiểu thời gian.
- Nếu thì hai sự kiện nằm trên tuyến thế giới kiểu không gian (space-like), đây là khoảng không thời gian giữa hai sự kiện mà một sự kiện nằm ngoài nón ánh sáng của sự kiện kia.
- Nếu thì hai sự kiện nằm trên tuyến thế giới không (null-world line), hay chúng nằm trên đường đi của ánh sáng.
- Bất biến Lorentz là đại lượng không đổi khi chúng ta chuyển từ hệ tọa độ này sang hệ tọa độ khác.
- Tenxơ mêtric Minkowski là
- với dấu mêtric . Trong thuyết tương đối rộng, các tenxơ mêtric thay thế cho tenxơ và vẫn đảm bảo đại lượng là bất biến Lorentz cục bộ. Đồng thời tenxơ mêtric cho phép nâng và hạ chỉ số của các tenxơ khác. Các phương trình vật lý viết dưới dạng phương trình tenxơ có một thuận lợi là dạng phương trình của nó không thay đổi khi chúng ta chuyển sang hệ tọa độ khác bất kỳ (thể hiện cho tính hiệp biến tổng quát và nguyên lý tương đương Einstein).[31]
Phương trình trường Einstein[sửa | sửa mã nguồn]
Tuy đã nhận ra được hình học Riemann là công cụ toán học cần thiết nhằm mô tả các hiệu ứng hấp dẫn, chúng ta còn cần phải xác định thêm những nguồn của trường hấp dẫn. Trong mô hình hấp dẫn Newton, nguồn hấp dẫn là khối lượng. Trong thuyết tương đối hẹp, khối lượng là một thành phần trong đại lượng tổng quát hơn là tenxơ năng lượng–động lượng, bao gồm mật độ năng lượng và mật độ động lượng cũng như ứng suất (bao gồm áp suất và lực cắt). Tenxơ năng lượng–động lượng không chứa năng lượng của trường hấp dẫn.[32] Nếu nguồn hấp dẫn trong thuyết tương đối rộng chỉ là khối lượng-năng lượng, thì chúng ta cần phải lựa chọn ưu tiên một hệ quy chiếu quán tính và do đó đòi hỏi tồn tại một hệ quy chiếu quán tính toàn cục, điều này là không được phép trong thuyết tương đối tổng quát. Nhờ nguyên lý tương đương Einstein, ngoài khối lượng, năng lượng thì ứng suất cũng trở thành một nguồn cho trường hấp dẫn. Và tenxơ ứng suất–năng lượng ngay lập tức tổng quát cho không thời gian cong và trở thành tenxơ miêu tả mật độ nguồn cho trường hấp dẫn. Để cho phép thu về trường hợp giới hạn của lực hấp dẫn Newton cổ điển, một cách tự nhiên chúng ta giả thiết rằng phương trình trường hấp dẫn liên hệ tenxơ ứng suất–năng lượng hạng hai với một tenxơ độ cong hạng hai gọi là tenxơ Ricci, tenxơ này có ý nghĩa vật lý miêu tả một trường hợp đặc biệt của hiệu ứng thủy triều: nó cho biết sự thay đổi thể tích của một đám nhỏ hạt thử ban đầu đứng yên tương đối với nhau, và sau đó rơi tự do trong trường hấp dẫn. Trong thuyết tương đối hẹp, định luật bảo toàn năng lượng–động lượng tương ứng với phương trình toán học là phân kỳ của tenxơ ứng suất–năng lượng phải bằng 0 (hay tự do). Công thức này cũng được tổng quát hóa sang cho không thời gian cong bằng cách thay thế đạo hàm riêng thông thường theo các trục tọa độ của đa tạp cong bằng đạo hàm hiệp biến của các tọa độ, đạo hàm này được nghiên cứu trong hình học vi phân. Các định luật bảo toàn phải luôn thỏa mãn ở phạm vi cục bộ — hay là phân kỳ hiệp biến của tenxơ mật độ ứng suất–năng lượng bằng 0, và do vậy phân kỳ hiệp biến của vế bên kia phương trình trường - vế cho biết độ cong cục bộ của không thời gian - cũng phải bằng 0. Ban đầu, Einstein nghĩ rằng vế hình học này chỉ có tenxơ Ricci (phân kỳ hiệp biến của tenxơ này khác 0), nhưng sau đó ông phát hiện ra phương trình trường cần phải tuân theo định lý phân kỳ hiệp biến tự do - và ông đã tìm ra dạng phương trình đơn giản nhất tuân theo định lý này, mà ngày nay gọi là Phương trình trường Einstein:
Vế trái của phương trình là tenxơ Einstein, phân kỳ hiệp biến của tenxơ này bằng 0. Tenxơ này là tổ hợp của tenxơ Ricci và tenxơ mêtric . Đặc biệt
là độ cong vô hướng Ricci, với có thể coi là các phần tử của ma trận nghịch đảo của ma trận có phần tử . Tenxơ Ricci liên hệ với tenxơ độ cong Riemann thông qua phép thu gọn chỉ số
Mặt khác, hệ số liên thông (hay ký hiệu Christoffel, nó không phải là tenxơ) có thể được tính từ tenxơ mêtric,
và tenxơ độ cong Riemann (miêu tả độ cong nội tại cục bộ của không thời gian) bằng
ở đây là đạo hàm riêng. Trong thuyết tương đối rộng, tenxơ độ xoắn bằng 0, do đó hệ số Christoffel có tính đối xứng cũng như tenxơ Ricci .
Trên vế phải của phương trình trường, là tenxơ mật độ ứng suất–năng lượng. Định luật bảo toàn năng lượng-động lượng cục bộ tương đương với phân kỳ hiệp biến (đạo hàm hiệp biến) của nó
với
- và
Tenxơ Einstein
và
Một khi giải phương trình Einstein và tìm được nghiệm là tenxơ mêtric (cho phép xác định được cấu trúc hình học của đa tạp không thời gian), chúng ta sẽ miêu tả được chuyển động của hạt (hay kể cả ánh sáng-photon) trong trường hấp dẫn thông qua phương trình đường trắc địa,
với là tham số của đường trắc địa. Tất cả các phương trình trên được viết trong hệ tọa độ bất kỳ. Tất cả các tenxơ và hệ số Christoffel có thành phần viết theo ký hiệu chỉ số trừu tượng, và tuân theo quy tắc tính tổng Einstein.[33] Để cho kết quả tiên đoán phù hợp với kết quả lý thuyết Newton về quỹ đạo các hành tinh và khi trường hấp dẫn yếu, Einstein tìm ra hằng số tỷ lệ trong phương trình κ = 8πG/c4, với G là hằng số hấp dẫn và c là tốc độ ánh sáng.[34] Khi không có vật chất hay bức xạ, tenxơ mật độ ứng suất–năng lượng bằng 0, và chúng ta thu được phương trình chân không Einstein,
do vô hướng độ cong R là hàm của tenxơ Ricci nên nó cũng bằng 0 trong phương trình chân không.
Ngoài cách dẫn ra phương trình Einstein tuân theo định luật bảo toàn năng lượng-động lượng ở trên, chính Einstein và nhà toán học David Hilbert còn nêu ra phương pháp biến phân cho tác dụng Einstein-Hilbert và cũng thu được phương trình trường. Phương pháp biến phân có đặc điểm là nó thuận lợi cho việc tổng quát hay mở rộng thuyết tương đối tổng quát.
Các nhà vật lý cũng đã đề xuất ra những lý thuyết khác so với thuyết tương đối tổng quát và thu được những phương trình trường khác nhau. Những lý thuyết này cũng dựa trên ba điều kiện mà thuyết tương đối tổng quát thỏa mãn:
- Các phương trình tuân theo nguyên lý hiệp biến tổng quát (và nguyên lý tương đương Einstein).
- Phương trình trường tuân theo định luật bảo toàn năng lượng-động lượng cục bộ đối với mọi tenxơ mêtric.
- Khi trường hấp dẫn yếu và vận tốc các vật thể là nhỏ so với tốc độ ánh sáng, lý thuyết sẽ thu về mô hình hấp dẫn Newton và cơ học cổ điển.
Ngoài ba điều kiện trên thì các lý thuyết này còn có thêm một số giả thiết khác, và do đó những lý thuyết đề xuất này phức tạp hơn về mặt toán học so với thuyết của Einstein. Ví dụ một số lý thuyết như thuyết Brans–Dicke, teleparallelism, và thuyết Einstein–Cartan (thuyết này coi tenxơ độ xoắn khác 0).[35]
Định nghĩa và các ứng dụng cơ bản[sửa | sửa mã nguồn]
Một số nét khái quát ở phần trước chứa mọi thông tin cần thiết để miêu tả thuyết tương đối rộng, các tính chất quan trọng của nó, những hệ quả chủ yếu và việc ứng dụng lý thuyết đề xây dựng các mô hình vật lý.
Định nghĩa và các tính chất cơ bản[sửa | sửa mã nguồn]
Thuyết tương đối tổng quát là lý thuyết mêtric về tương tác hấp dẫn. Phương trình nền tảng của lý thuyết là phương trình trường Einstein, trong đó liên hệ giữa hình học của đa tạp tựa Riemann bốn chiều của không thời gian với năng lượng và động lượng chứa trong không thời gian đó.[36] Những quá trình hiện tượng trong cơ học cổ điển được gán cho nguyên nhân lực hấp dẫn tác dụng (như vật rơi tụ do, chuyển động trên quỹ đạo của các hành tinh, và quỹ đạo của các vệ tinh nhân tạo), tương ứng với chuyển động quán tính trong hình học cong của không thời gian trong thuyết tương đối rộng; không có lực hấp dẫn làm lệch quỹ đạo chuyển động của vật khỏi đường thẳng. Thay vào đó, lực hấp dẫn là do sự thay đổi tính chất của không thời gian, dẫn đến làm thay đổi quỹ đạo của vật trở thành đường "ngắn nhất" có thể mà vật sẽ tự nhiên chuyển động theo (hay đường trắc địa trong hình học vi phân).[37] Còn nguồn gốc độ cong của không thời gian là do năng lượng và động lượng của vật chất. Như nhà vật lý John Archibald Wheeler phát biểu, không thời gian nói cho vật chất cách chuyển động; vật chất nói cho không thời gian cong như thế nào.[38]
Khi mà thuyết tương đối thay thế năng hấp dẫn vô hướng của vật lý cổ điển thành tenxơ đối xứng hạng hai, thì đồng thời tenxơ này sẽ thu về trường hợp giới hạn cổ điển trong những điều kiện xác định. Đối với trường hấp dẫn yếu và chuyển động có vận tốc tương đối chậm so với tốc độ ánh sáng, lý thuyết cho kết quả tiên đoán trùng với tiên đoán của định luật vạn vật hấp dẫn Newton.[39]
Được xây dựng trên công cụ tenxơ, thuyết tương đối tổng quát thể hiện tính hiệp biến tổng quát: mỗi định luật của nó và hơn nữa các định luật thiết lập trên khuôn khổ tương đối tính tổng quát—sẽ có dạng phương trình như nhau trong mọi hệ tọa độ.[40] Căn bản hơn, lý thuyết không chứa bất kỳ một cấu trúc hình học cơ sở bất biến nào, hay thuyết tương đối rộng có đặc tính độc lập với phông cơ sở không thời gian (ứng với mỗi sự phân bố vật chất và năng lượng thì lại có một dạng hình học không thời gian khác nhau). Nó cũng thỏa mãn điều kiện chặt chẽ của nguyên lý tương đối tổng quát, tức là mọi định luật vật lý phải như nhau đối với mọi quan sát viên.[41] Trên cục bộ, như đòi hỏi của nguyên lý tương đương, không thời gian cong trở thành không thời gian Minkowski, và các định luật vật lý tuân theo bất biến Lorentz cục bộ.[42]
Cơ sở cho mô hình vật lý[sửa | sửa mã nguồn]
Khái niệm cốt lõi trong mô hình vật lý tương đối tính tổng quát đó là tìm nghiệm của phương trình trường Einstein. Khi có phương trình Einstein và những phương trình hay điều kiện giới hạn cụ thể khác về tính chất của vật chất (như phương trình trạng thái, hoặc giả định về tính đối xứng của không thời gian, hoặc phương trình điều kiện biên, điều kiện ban đầu) thì nghiệm của phương trình sẽ là một đa tạp tựa Riemann (thông thường đa tạp này được xác định bởi tenxơ mêtric theo những hệ tọa độ đặc biệt), và trường vật chất cụ thể xác định trên đa tạp đó. Vật chất cũng phải thỏa mãn bất kỳ một điều kiện phụ nào của các phương trình khác mô tả tính chất của nó. Hay ngắn gọn, mỗi nghiệm là một mô hình vật lý thỏa mãn các định luật tương đối tính tổng quát cũng như các định luật vật lý khác chi phối sự có mặt của vật chất.[43]
Phương trình trường Einstein là hệ phương trình vi phân riêng phần phi tuyến cho những kết quả đáng tin cậy, do vậy rất khó để tìm được nghiệm chính xác.[44] Tuy vậy, các nhà vật lý đã giải được một số nghiệm chính xác, mặc dầu chỉ có vài ba nghiệm có ý nghĩa vật lý trực tiếp.[45] Những nghiệm chính xác nổi tiếng nhất, và cũng có nhiều ứng dụng trong vật lý thực nghiệm đó là: mêtric Schwarzschild, mêtric Reissner–Nordström và mêtric Kerr, chúng là các nghiệm của phương trình chân không Einstein và mỗi nghiệm tương ứng với một kiểu lỗ đen;[46] và mêtric Friedmann–Lemaître–Robertson–Walker và "vũ trụ de Sitter", mỗi loại miêu tả một vũ trụ có tính động lực.[47] Những nghiệm chính xác hấp dẫn về mặt lý thuyết bao gồm "vũ trụ Gödel" (mở ra khả năng kỳ lạ cho phép du hành ngược thời gian trong không thời gian cong), "nghiệm sóng-pp" cho sóng hấp dẫn, "không gian Taub-NUT" (mô hình vũ trụ đồng nhất, nhưng phi đẳng hướng), và "không gian phản de Sitter" (mà gần đây trở lên quan trọng trong "phỏng đoán Maldacena" của lý thuyết dây).[48]
Do rất khó để tìm được nghiệm chính xác, các nhà vật lý đã tìm cách giải phương trình trường Einstein bằng phương pháp "tích phân số" trên máy tính, hoặc xét những nhiễu loạn nhỏ trong nghiệm chính xác. Trong lĩnh vực mô phỏng lý thuyết bằng máy tính, người ta sử dụng các siêu máy tính để mô phỏng hình học của không thời gian và giải phương trình Einstein cho những tình huống quan trọng như sự va chạm và sáp nhập hai lỗ đen hay cấu trúc của vũ trụ trên khoảng cách lớn.[49] Đặc biệt, phương pháp này có thể áp dụng cho một hệ bất kỳ nếu khả năng tính toán của siêu máy tính cho phép, và có thể tiếp cận được những câu hỏi căn bản như điểm kỳ dị hấp dẫn. Chúng ta có thể tìm những nghiệm xấp xỉ bằng lý thuyết nhiễu loạn như "tuyến tính hóa hấp dẫn"[50] và phương pháp tổng quát hóa của nó "khai triển hậu Newton", cả hai phương pháp này đều do Einstein phát triển. Phương pháp sau cung cấp cách tiếp cận có hệ thống nhằm giải ra hình học không thời gian với sự phân bố vật chất chuyển động chậm so với tốc độ ánh sáng. Phương pháp khai triển chứa các chuỗi số hạng; với số hạng thứ nhất đại diện cho đóng góp của hấp dẫn Newton, trong khi những số hạng tiếp sau thể hiện những hiệu chỉnh nhỏ hơn của lý thuyết Newton từ thuyết tương đối tổng quát.[51] Phương pháp mở rộng của phương pháp này gọi là "hình thức tham số hóa hậu Newton", cho phép so sánh một cách định lượng giữa những tiên đoán của thuyết tương đối rộng với những lý thuyết thay thế phi lượng tử khác.[52]
- Nghiệm Schwarzchild: miêu tả không thời gian tĩnh có tính đối xứng cầu, bên ngoài bán kính Schwarzchild. Nó là nghiệm của phương trình chân không với
- Trong hệ tọa độ cầu sử dụng dấu mêtric (-, +, +, +), mêtric Schwarzchild là [53]
- với
- τ là thời gian riêng (đo bởi đồng hồ gắn cùng với hạt thử di chuyển trên tuyến thế giới kiểu thời gian)
- t là tọa độ thời gian (đo bởi một đồng hồ đứng yên nằm rất xa so với nguồn hấp dẫn),
- r là tọa độ xuyên tâm (đo bằng chu vi đường tròn chia cho 2π, các đường tròn nằm trên mặt cầu có tâm tại nguồn hấp dẫn),
- θ là độ dư vĩ (tính từ cực bắc, đơn vị radian),
- φ là kinh độ (radian), và
- rs là bán kính Schwarzschild của nguồn hấp dẫn, nó là hệ số tỷ lệ liên hệ với khối lượng M của "nguồn hấp dẫn không có điện tích và không quay" và rs = 2GM/c2.[54]
- hay dạng ma trận của mêtric
- Ta thấy khi hạt thử nằm rất xa nguồn hấp dẫn hoặc khi không có nguồn hấp dẫn thì mêtric Schwarzschild trở thành mêtric Minkowski sau khi chuyển từ tọa độ cầu sang tọa độ (ct, x, y, z).
- Tỷ số rs/r là rất nhỏ, đối với Mặt Trời có bán kính Schwarzschild xấp xỉ 3 km, trong khi nó có bán kính gần 700.000 km. Tỷ số này sẽ tương đối lớn đối với lỗ đen và sao neutron. Ta thấy tại r = rs thì mêtric trở lên kỳ dị (còn gọi là chân trời sự kiện), thực ra đây là kỳ dị do chúng ta sử dụng hệ tọa độ cầu chứ không hẳn là kỳ dị thực. Khi lựa chọn hệ tọa độ phù hợp, kỳ dị này biến mất và chỉ có r = 0 mới là điểm kỳ dị vật lý.
Hệ quả của lý thuyết Einstein[sửa | sửa mã nguồn]
Thuyết tương đối rộng có một số hệ quả vật lý. Một số xuất hiện trực tiếp từ những tiên đề của lý thuyết, trong khi một số khác chỉ trở lên rõ ràng sau hơn 100 năm nghiên cứu kể từ khi Einstein công bố lý thuyết này.
Sự giãn thời gian do hấp dẫn và dịch chuyển tần số[sửa | sửa mã nguồn]

Ban đầu, bằng giả sử nguyên lý tương đương là thỏa mãn,[55] Einstein đã chứng tỏ trường hấp dẫn ảnh hưởng tới sự trôi đi của thời gian. Khi ánh sáng truyền vào trường hấp dẫn mạnh thì tần số của nó tăng lên (hay bước sóng giảm đi-dịch chuyển xanh), trong khi ánh sáng truyền theo hướng ngược lại-thoát ra khỏi trường hấp dẫn thì tần số của nó giảm (hay bước sóng tăng-dịch chuyển đỏ); kết hợp lại, hai hiệu ứng này gọi chung là dịch chuyển tần số do hấp dẫn. Tần số ánh sáng trong một hệ quy chiếu cục bộ cũng chính là thời gian đo được trong hệ quy chiếu đó. Do vậy, tổng quát hơn, một quá trình sẽ diễn ra chậm chạp khi gần thiên thể khối lượng lớn so với cùng quá trình đó diễn ra ở một nơi xa hơn; hiệu ứng này gọi là sự giãn thời gian do hấp dẫn-hay nói về mặt hình học, thời gian bị cong do sự có mặt của vật chất.[56]
Hiệu ứng dịch chuyển đỏ đã được đo trong phòng thí nghiệm[57] và ở những quan sát thiên văn.[58] Sự giãn thời gian trong trường hấp dẫn của Trái Đất cũng được đo nhiều lần bằng các đồng hồ nguyên tử,[59] và nhờ hiệu chỉnh sai lệch thời gian do hiệu ứng này cho phép Hệ thống định vị toàn cầu (GPS) hoạt động chính xác tới vài mét.[60] Những kiểm nghiệm trong trường hấp dẫn mạnh thực hiện trên quan sát các pulsar đôi.[61] Tất cả các kết quả thí nghiệm và quan sát đều phù hợp với thuyết tương đối tổng quát với sai số nhỏ.[62] Tuy vậy, ở mức độ chính xác hiện nay, những quan sát này không thể loại trừ một số lý thuyết thay thế thuyết tương đối rộng cũng dựa trên nguyên lý tương đương, và một số lý thuyết thì bị bác bỏ.[63]
Ánh sáng bị lệch và sự trễ thời gian do hấp dẫn[sửa | sửa mã nguồn]
Thuyết tương đối tổng quát tiên đoán quỹ đạo của ánh sáng bị bẻ cong trong trường hấp dẫn; ánh sáng lan truyền gần vật thể khối lượng lớn bị kéo về phía vật đó. Hiệu ứng này đã được xác nhận từ các quan sát ánh sáng phát ra từ những ngôi sao, thiên hà hay quasar ở xa bị lệch đi khi đi gần Mặt Trời.[64]
Hiệu ứng này và những tiên đoán liên quan là do thực tế ánh sáng truyền theo đường trắc địa kiểu ánh sáng hay đường trắc địa không—một đường tổng quát hóa những đường thẳng mà ánh sáng truyền đi trong vật lý cổ điển. Những đường trắc địa này cũng là sự tổng quát hóa tính bất biến của tốc độ ánh sáng trong thuyết tương đối hẹp.[65] Khi chúng ta khảo sát các mô hình không thời gian một cách phù hợp (hoặc là phía bên ngoài bán kính Schwarzschild, hoặc khi có nhiều vật thể tham gia thì sử dụng phương pháp khai triển hậu Newton),[66] thì một vài hiệu ứng của hấp dẫn lên sự lan truyền của ánh sáng xuất hiện. Mặc dầu hiện tượng lệch ánh sáng có thể suy ra được khi chúng ta xét ánh sáng truyền trong một hệ quy chiếu đang rơi tự do,[67] nhưng kết quả tính thu được cho góc lệch chỉ bằng một nửa giá trị so với kết quả của thuyết tương đối rộng.[68]
Một hiệu ứng có liên hệ gần gũi với ánh sáng bỉ bẻ cong là hiệu ứng trễ thời gian do hấp dẫn (hay trễ Shapiro), hiện tượng tín hiệu ánh sáng truyền từ điểm A tới điểm B sẽ mất thời gian lâu hơn nếu có một trường hấp dẫn giữa hai điểm đó so với khi không có trường hấp dẫn. Đã có nhiều thí nghiệm thành công kiểm tra hiệu ứng này với độ chính xác cao.[69] Trong phương pháp tham số hóa hậu Newton (PPN), các phép đo bao gồm cả độ lệch ánh sáng và độ trễ thời gian do hấp dẫn xác định một tham số γ, chứa sự ảnh hưởng của trường hấp dẫn lên hình học của không gian.[70]
Sóng hấp dẫn[sửa | sửa mã nguồn]

Có một vài điểm tương tự giữa trường hấp dẫn yếu và điện từ học đó là, sự tương tự giữa sóng điện từ và sóng hấp dẫn: những biến đổi nhỏ của mêtric của không thời gian lan truyền với tốc độ ánh sáng.[71] Hình dung đơn giản nhất về sóng hấp dẫn có thể thấy là tác dụng của nó lên vành hạt thử đặt trong vùng sóng truyền qua. Sóng hình sin lan truyền qua vành hạt theo hướng vuông góc với mặt phẳng vành làm bóp méo vành theo kiểu dao động điều hòa (minh họa hình bên phải).[72] Do phương trình trường Einstein là phi tuyến, sóng hấp dẫn có cường độ bất kỳ không tuân theo nguyên lý chồng chập, khiến cho việc miêu tả nó rất khó khăn. Tuy vậy, đối với trường yếu chúng ta có thể áp dụng phương pháp xấp xỉ tuyến tính. Những sóng hấp dẫn được tuyến tính hóa là đủ chính xác để miêu tả các loại sóng lan truyền đến Trái Đất từ những sự kiện vũ trụ từ rất xa nếu các máy dò phát hiện ra chúng. Khi đến Trái Đất, do nguồn sản sinh ra sóng hấp dẫn ở rất xa cho nên biên độ sóng thu được ở các máy dò được tính toán vào khoảng cỡ hay nhỏ hơn. Các phương pháp phân tích dữ liệu thu được từ máy dò sử dụng đặc điểm của sóng hấp dẫn tuyến tính hóa đó là chúng có thể phân tích thành tổng các chuỗi tuần hoàn, hay chuỗi Fourier.[73]
Một số nghiệm chính xác miêu tả sóng hấp dẫn mà không cần đến phương pháp xấp xỉ, như đoàn sóng truyền qua chân không[74] còn gọi là "vũ trụ Gowdy", một loại vũ trụ đang giãn nở chứa đầy sóng hấp dẫn.[75] Nhưng đối với sóng hấp dẫn sinh ra từ những sự kiện thiên văn vật lý, như hai lỗ đen quay trên quỹ đạo quanh nhau và cuối cùng sáp nhập lại, hoặc các vụ nổ siêu tân tinh, những sự kiện này chỉ có thể thực hiện mô phỏng trên siêu máy tính bằng các mô hình phù hợp.[76]
Ngày 11 tháng 2 năm 2016, nhóm Hợp tác Khoa học LIGO và Virgo thông báo đã đo được trực tiếp sóng hấp dẫn phát ra từ cặp lỗ đen khối lượng sao sáp nhập vào nhau mở ra một lĩnh vực mới đó là thiên văn sóng hấp dẫn.[77][78][79]
Hiệu ứng quỹ đạo và tính tương đối của phương hướng[sửa | sửa mã nguồn]
Thuyết tương đối tổng quát tiên đoán một số kết quả khác lạ về chuyển động quỹ đạo của vật thể so với cơ học cổ điển. Nó tiên đoán sự tiến động của điểm cận nhật của quỹ đạo hành tinh, cũng như sự giảm chu kỳ quỹ đạo do hệ phát ra sóng hấp dẫn và các hiệu ứng liên quan đến tính tương đối của phương hướng.
Sự tiến động của điểm cận nhật[sửa | sửa mã nguồn]

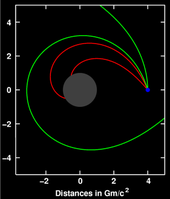
Trong thuyết tương đối rộng, cận điểm quỹ đạo (điểm của quỹ đạo gần nhất với khối tâm của hệ) sẽ tiến động—hay quỹ đạo không phải là elip, mà gần giống với elip khi nó quay quanh khối tâm, mà sẽ là đường cong giống cánh hoa hồng (xem hình bên). Einstein lần đầu tiên tìm ra được kết quả này khi ông sử dụng phương pháp xấp xỉ mêtric về giới hạn Newton và coi hành tinh có khối lượng không đáng kể so với Mặt Trời. Đối với ông, kết quả tính toán lượng dịch chuyển điểm cận nhật của Sao Thủy bằng với giá trị mà nhà thiên văn Urbain Le Verrier phát hiện ra vào năm 1859, chính là điều củng cố cho ông tin rằng cuối cùng ông đã tìm ra dạng đúng của phương trình trường hấp dẫn.[80]
Hiệu ứng này có thể suy trực tiếp từ nghiệm chính xác là mêtric Schwarzschild (miêu tả không thời gian xung quanh vật thể khối lượng hình cầu)[81] hoặc sử dụng phương pháp khai triển hậu Newton.[82] Về bản chất hiệu ứng dịch chuyển điểm cận nhật là do ảnh hưởng của hấp dẫn lên hình học của không gian và sự đóng góp của năng lượng tự có (self-energy) của nguồn hấp dẫn (thể hiện bởi tính phi tuyến của phương trình trường Einstein).[83] Sự tiến động cận điểm đã được quan sát cho một số hành tinh với độ chính xác cao (Sao Thủy, Sao Kim và Trái Đất),[84] cũng như ở hệ đôi pulsar, mà ở đây hiệu ứng thể hiện rõ cỡ vài bậc độ lớn.[85]
Giảm chu kỳ quỹ đạo[sửa | sửa mã nguồn]

Theo thuyết tương đối tổng quát, hệ sao đôi sẽ phát ra sóng hấp dẫn và vì vậy hệ mất năng lượng. Vì sự mất mát này, khoảng cách quỹ đạo giữa hai vật thể sẽ giảm dần, và tương ứng là chu kỳ quỹ đạo. Trong hệ Mặt Trời hoặc ở những hệ sao đôi, hiệu ứng này rất nhỏ và khó quan sát được. Nhưng đối với hệ pulsar đôi gồm hai sao neutron quay quanh nhau, trong đó có một hoặc cả hai là pulsar: những đài thiên văn vô tuyến trên Trái Đất sẽ nhận được những xung vô tuyến rất đều đặn từ các pulsar này, chúng được coi là những đồng hồ chính xác nhất trong tự nhiên, và cho phép việc đo các tham số quỹ đạo của hệ trở lên rất chính xác. Do sao neutron là những vật thể nén đặc và quay quanh nhau ở khoảng cách nhỏ cho nên lượng năng lượng của sóng hấp dẫn chúng phát ra là đáng kể.[87]
Hai nhà thiên văn vô tuyến Hulse và Taylor là những người đầu tiên ghi nhận sự suy giảm chu kỳ quỹ đạo do phát ra sóng hấp dẫn từ hệ pulsar PSR1913+16 mà họ đã phát hiện ra năm 1974. Đây là khám phá gián tiếp ra sóng hấp dẫn đầu tiên và họ nhận giải Nobel Vật lý vì khám phá này.[88] Từ đó tới nay, các nhà thiên văn đã phát hiện ra một vài hệ pulsar đôi khác, đặc biệt hệ PSR J0737-3039 chứa cả hai pulsar.[89]
Hiệu ứng trắc địa và kéo hệ quy chiếu[sửa | sửa mã nguồn]
Có một số hiệu ứng tương đối tính tổng quát liên quan trực tiếp đến tính tương đối của phương hướng.[90] Một hiệu ứng đó là độ lệch trắc địa: trục quay của một con quay trong không thời gian cong sẽ bị lệch đi trong quá trình con quay di chuyển trên quỹ đạo khi so sánh hướng của nó với một vật cố định ở rất xa, như ngôi sao chẳng hạn—cho dù con quay cố giữ hướng trục quay của nó cố định một hướng. Hiệu ứng này thể hiện bằng toán học chính là quá trình "chuyển dịch song song" của một vectơ trên đường trắc địa trong đa tạp cong.[91] Đối với hệ Mặt Trăng–Trái Đất, khi coi Mặt Trăng là một "vectơ", hiệu ứng này đã được đo bằng cách chiếu tia laser lên một tấm phản quang đặt trên Mặt Trăng do các nhà du hành vũ trụ để lại khi đổ bộ lên Mặt Trăng (phương pháp định tầm Mặt Trăng).[92] Gần đây, hiệu ứng trắc địa đã được đo với độ chính xác hơn 0,3% từ bốn con quay hồi chuyển siêu dẫn đặt trên vệ tinh Gravity Probe B quay trên quỹ đạo cực quanh Trái Đất.[93][94]
Trường hấp dẫn gần một thiên thể quay quanh trục của nó có tính động lực cao, hiệu ứng này gọi là hấp dẫn từ hay hiệu ứng kéo hệ quy chiếu. Một quan sát viên ở vị trí xa sẽ nhận thấy vật thử ở gần thiên thể quay bị "kéo theo" chiều quay của thiên thể đó. Hiện ứng này thể hiện rất rõ ở vùng không thời gian quanh lỗ đen quay, vùng này được miêu tả bằng mêtric Kerr. Khi ta một vật đặt vào "vùng sản công" của lỗ đen, việc nó bị kéo theo chiều quay của lỗ đen là không thể tránh khỏi.[95] Sử dụng hướng của các con quay hồi chuyển trên đường trắc địa ta cũng thực hiện được kiểm nghiệm hiệu ứng này.[96] Có một số thử nghiệm gây tranh cãi khi các nhà vật lý sử dụng vệ tinh LAGEOS để kiểm nghiệm xác nhận hiệu ứng này.[97] Tàu thăm dò Mars Global Surveyor thám hiểm Sao Hỏa cũng đã được sử dụng để kiểm tra hiệu ứng này.[98][99] Kết quả thí nghiệm từ tàu Gravity Probe B cũng xác nhận hiệu ứng này với độ chính xác khoảng 15%.[94]
Các ứng dụng thiên văn vật lý[sửa | sửa mã nguồn]
Thấu kính hấp dẫn[sửa | sửa mã nguồn]

Sự lệch ánh sáng do hấp dẫn dẫn đến một hiện tượng thiên văn vật lý mới. Nếu có một thiên thể khối lượng lớn nằm giữa kính thiên văn và vật thể ở xa thì chúng ta sẽ thu được nhiều hình ảnh bị méo mó của vật này. Hiệu ứng này được gọi là thấu kính hấp dẫn.[100] Phụ thuộc vào khoảng cách, nguồn phát, và sự phân bố khối lượng của thiên thể thấu kính, chúng ta có thể thu được nhiều hơn hai ảnh, hay thậm chí là một vành tròn gọi là vành Einstein, hoặc dạng cung.[101] Các nhà thiên văn lần đầu tiên phát hiện ra thấu kính hấp dẫn vào năm 1979;[102] Kể từ đó tới nay, hàng trăm thấu kính hấp dẫn đã được phát hiện và nghiên cứu.[103] Ngay cả khi nhiều hình ảnh của cùng vật thể hiện ra quá gần nhau trong bức ảnh chụp, các nhà khoa học vẫn đo được hiệu ứng này, ví dụ, do đối tượng mục tiêu quá sáng; hiệu ứng "vi thấu kính hấp dẫn" đã được quan sát thấy.[104]
Thấu kính hấp dẫn trở thành một công cụ quan trọng trong thiên văn quan sát. Các nhà vũ trụ học sử dụng nó để phát hiện và ước tính sự phân bố của vật chất tối, họ sử dụng "thấu kính tự nhiên" để quan sát các thiên hà ở xa và có được phương pháp độc lập nhằm ước tính hằng số Hubble. Nhờ phân tích, đánh giá thống kê từ dữ liệu các thấu kính đã cung cấp những manh mối quan trọng trong sự tiến hóa cấu trúc của các thiên hà.[105]
Thiên văn sóng hấp dẫn[sửa | sửa mã nguồn]

Bằng quan sát các hệ pulsar đôi đã cung cấp những kết quả gián tiếp khẳng định sự tồn tại của sóng hấp dẫn (xem phần Giảm chu kỳ quỹ đạo ở trên). Sóng hấp dẫn phát ra từ những nguồn xa xôi trong vũ trụ đã được quan sát trực tiếp (như các sự kiện GW150914 và GW151226), và là mục tiêu chính của các dự án nghiên cứu liên quan đến thuyết tương đối hiện nay.[77][78][106] Vài trạm quan sát thăm dò sóng hấp dẫn đang hoạt động trên mặt đất, nổi bật là các máy dò sóng hấp dẫn sử dụng giao thoa kế laser như GEO 600, LIGO, TAMA 300 và VIRGO.[107] Nhiều kính thiên văn vô tuyến quan sát sự biến đổi nhỏ trong chu kỳ quay của các pulsar mili giây nhằm phát hiện sóng hấp dẫn ở dải tần số 10−9 đến 10−6 Hertz phát ra từ sự kiện sáp nhập hai lỗ đen.[108] Đài quan sát châu Âu trên không gian, eLISA/NGO, hiện tại đang được phát triển,[109] với phi vụ thử nghiệm tiên phong (LISA Pathfinder) được phóng lên vào năm 2015,[110] và đã thu được kết quả thí nghiệm vượt mong đợi của các nhà khoa học.[111][112][113]
Quan sát sóng hấp dẫn cũng hứa hẹn bổ sung cho dữ liệu quan sát từ sóng điện từ.[114] Chúng cho phép các nhà vật lý thu được thông tin về các lỗ đen và những thiên thể nén đặc khác như sao neutron và sao lùn trắng, về sự kiện phát nổ siêu tân tinh, và giai đoạn hình thành còn sơ khai của vũ trụ, bao gồm dấu hiệu của loại "dây vũ trụ" được các nhà lý thuyết dự đoán.[115]
Lỗ đen và các thiên thể nén đặc[sửa | sửa mã nguồn]

Bất cứ khi nào tỉ số giữa khối lượng của vật và bán kính của nó trở lên đủ lớn vượt qua một giới hạn, các nhà lý thuyết tiên đoán sẽ hình thành một lỗ đen, vùng của không thời gian mà không một thứ gì, kể cả ánh sáng có thể thoát ra được. Trong những mô hình được chấp nhận hiện nay về quá trình tiến hóa sao, các sao neutron với khối lượng xấp xỉ 1,4 lần khối lượng Mặt Trời, và các lỗ đen có khối lượng từ vài lần đến vài chục lần khối lượng Mặt Trời được cho là trạng thái cuối cùng trong quá trình tiến hóa của các ngôi sao có khối lượng lớn.[116] Tại tâm của các thiên hà thường có lỗ đen siêu khối lượng với khối lượng từ vài triệu tới một chục tỷ lần khối lượng Mặt Trời,[117] và sự có mặt của nó được cho là có vai trò quan trọng trong quá trình hình thành thiên hà cũng như các cấu trúc ở cấp độ lớn hơn.[118]

Về mặt thiên văn vật lý, tính chất quan trọng nhất của các thiên thể nén đặc là chúng cung cấp một cơ chế hiệu quả rất cao cho sự biến đổi năng lượng hấp dẫn thành bức xạ điện từ.[119] Quá trình bồi tụ, vật chất khí hay bụi bị thu hút về các lỗ đen, là nguyên nhân phát sáng rất mạnh của một số thiên thể, điển hình là nhân các thiên hà hoạt động trên quy mô thiên hà hoặc các vi quasar ở những thiên thể cấp độ sao.[120] Đặc biệt, sự bồi tụ cũng dẫn đến hình thành chùm tia tương đối tính, chùm hạt và bức xạ năng lượng cao với các hạt bị bắn ra với vận tốc gần bằng tốc độ ánh sáng.[121] Thuyết tương đối tổng quát đóng một vai trò quan trọng cho mô hình hóa tất cả những hiện tượng này,[122] và nhiều quan sát đã cung cấp những bằng chứng thực nghiệm cho sự tồn tại của lỗ đen với tính chất phù hợp với tiên đoán của lý thuyết.[123]
Lỗ đen cũng là mục tiêu mong muốn tìm kiếm trong nghiên cứu sóng hấp dẫn (xem phần sóng hấp dẫn ở trên). Quá trình sáp nhập các hệ lỗ đen đôi sẽ phát ra sóng hấp dẫn với tín hiệu rất mạnh khi đến được máy dò trên Trái Đất, và sóng hấp dẫn phát ra ở giai đoạn trước khi hai lỗ đen trộn thành một có thể coi là "ngọn nến chuẩn" nhằm đo khoảng cách đến hệ lỗ đen và cung cấp phương pháp độc lập cho nghiên cứu sự giãn nở của vũ trụ ở khoảng cách lớn.[124] Sóng hấp dẫn phát ra từ sự kiện lỗ đen khối lượng sao bị hút vào lỗ đen siêu khối lượng mang lại cho các nhà vật lý thông tin về hình học của lỗ đen lớn hơn.[125]
Vũ trụ học[sửa | sửa mã nguồn]


Mô hình chuẩn về vũ trụ học hiện nay dựa trên phương trình trường Einstein có chứa hằng số vũ trụ học Λ, do nó có ảnh hưởng quan trọng đến động lực trên quy mô lớn của vũ trụ,
với là tenxơ mêtric.[126] Dựa trên Nguyên lý vũ trụ học, vũ trụ là đồng nhất và đẳng hướng trên quy mô lớn, các nhà vật lý tìm ra được mêtric Friedmann–Lemaître–Robertson–Walker (mêtric FLRW) là nghiệm chính xác của phương trình Einstein mô tả vũ trụ đang nở ra hay co lại,[127] cho phép mô tả sự tiến hóa của vũ trụ từ xấp xỉ 13,8 tỷ năm về trước, khởi nguyên từ Vụ Nổ Lớn.[128] Mêtric FLRW là:[129]
với a(t) là hệ số tỷ lệ chỉ phụ thuộc thời gian, hằng số k phụ thuộc vào độ cong của không thời gian và được chuẩn hóa thành -1, 0, 1 tương ứng với mô hình vũ trụ mở, phẳng hay đóng. Các biến là các tọa độ đồng chuyển động, mà mỗi thiên hà có giá trị cố định riêng. Khoảng cách vũ trụ học vật lý (khoảng cách thực) đối với hai thiên hà cách nhau một khoảng r và ở thời gian t cho trước (trong mô hình vũ trụ phẳng k = 0) là a(t)r, mà tăng dần theo thời gian đối với vũ trụ đang giãn nở. Để xác định được hệ số a(t), chúng ta phải giải phương trình Einstein với mêtric FLRW (thực chất mêtric là dạng tổng quát đối với vũ trụ có tính đồng nhất và đẳng hướng, nó không nhất thiết suy ra từ phương trình Einstein, phương trình này cần thiết để tính ra hệ số a(t)) gắn với dạng phân bố của vật chất.[129] Theo Nguyên lý vũ trụ học hàm ý tenxơ mật độ năng lượng-động lượng của vật chất và bức xạ trong vũ trụ có dạng giống với tenxơ mật độ năng lượng-động lượng của chất lỏng tương đối tính lý tưởng có mật độ và áp suất (cả hai có thể biến đổi theo thời gian) và tenxơ mật độ năng lượng-động lượng có dạng
với là bốn vận tốc của vật chất, và là thành phần của ma trận nghịch đảo của ma trận có thành phần . Tiếp theo, sử dụng mêtric chúng ta tính ra được hệ số Christoffel và tenxơ Ricci, vô hướng Ricci. Cùng với tenxơ mật độ năng lượng-động lượng thay vào phương trình trường Einstein chúng ta thu được hai phương trình Friedmann độc lập sau khi sắp xếp lại các số hạng[129]
với a chấm có nghĩa là đạo hàm theo thời gian của a và H là tốc độ giãn nở của Vũ trụ gọi là tham số Hubble hay hằng số Hubble (giá trị hiện tại của nó là , và hay có dạng tương tự như thường viết ở định luật Hubble). Từ hai phương trình ta thấy H phụ thuộc vào cả mật độ năng lượng, độ cong của không thời gian cũng như hằng số . Nếu hằng số vũ trụ học lấn át mật độ năng lượng, bức xạ của vật chất (cả vật chất tối và vật chất thường) trong vũ trụ thì ở phương trình Friedmann thứ hai có vế trái lớn hơn 0 và dẫn đến sự giãn nở của vũ trụ tăng tốc. Ngoài hai phương trình trên chúng ta còn có thêm phương trình của định luật bảo toàn
Phương trình Friedmann có thể giải chính xác khi giả sử thêm phương trình trạng thái của chất lỏng lý tưởng
với là áp suất, là mật độ của chất lỏng trong hệ tọa độ đồng chuyển động và là hằng số.
Trong trường hợp vũ trụ phẳng (k = 0) và khi Λ=0, nghiệm cho hệ số tỷ lệ là
với là hằng số tích phân tuân theo lựa chọn điều kiện đầu. Họ nghiệm cho tham số là rất quan trọng trong mô hình vũ trụ học.

Khi các tham số (như mật độ trung bình của vật chất, áp suất bức xạ...) được đo từ các dự án khảo sát vũ trụ,[130] và phối hợp với các dữ liệu khác nhằm kiểm tra các hệ quả mà mô hình chuẩn vũ trụ học tiên đoán.[131] Các hệ quả tiên đoán, hầu hết phù hợp với dữ liệu quan sát, bao gồm lượng nguyên tố hóa học hình thành trong giai đoạn tổng hợp hạt nhân nguyên thủy của vũ trụ sơ khai từ Vụ Nổ Lớn,[132] cấu trúc lớn của vũ trụ,[133] cũng như sự tồn tại và tính chất của "tiếng vọng nhiệt" từ thời điểm khởi nguyên của vũ trụ, bức xạ phông vi sóng vũ trụ.[134]
Các dự án khảo sát tốc độ giãn nở của vũ trụ cho phép các nhà vật lý ước tính được tổng lượng vật chất trong vũ trụ, mặc dù bản chất của một số loại vẫn còn là bí ẩn. Khoảng 90% lượng vật chất là vật chất tối, mà có tương tác hấp dẫn, nhưng lại không tham gia vào tương tác điện từ, và do vậy không thể quan sát trực tiếp được.[135] Chưa có một lý thuyết nào miêu tả dạng vật chất mới này, mà phù hợp với khuôn khổ của Mô hình chuẩn trong vật lý hạt[136] hoặc phải đề xuất lý thuyết sửa đổi mô hình hấp dẫn.[137] Dữ liệu thu được từ các dự án khảo sát dịch chuyển đỏ từ các vụ nổ siêu tân tinh từ xa và đo lường từ bức xạ nền vi sóng cũng chỉ ra quá trình tiến hóa của vũ trụ bị ảnh hưởng lớn bởi hằng số vũ trụ học gây ra sự giãn nở tăng tốc của vũ trụ (miêu tả khái quát ở trên), hay tương đương, bởi một dạng năng lượng kỳ lạ kết hợp trong phương trình trạng thái, gọi là năng lượng tối, mà bản chất của nó vẫn chưa biết được.[138]
Có một giai đoạn xảy ra rất nhanh từ vụ nổ lớn đó là pha lạm phát,[139] một giai đoạn giãn nở gia tốc cực nhanh của vũ trụ trong khoảng thời gian cực ngắn giây. Nó được nêu ra từ năm 1980 với mục đích giải thích một số kết quả quan sát không là hệ quả của mô hình vũ trụ học cổ điển, như sự đồng nhất gần như hoàn hảo của bức xạ nền vũ trụ.[140] Những khảo sát gần đây về bức xạ nền vi sóng vũ trụ cho kết quả về chứng cứ đầu tiên của kịch bản này.[141] Tuy thế, có nhiều kịch bản lạm phát khác nhau mà hiện tại chưa thể nói kịch bản nào là phù hợp nhất nếu rút ra từ dữ liệu thực nghiệm.[142] Một câu hỏi lớn hơn nữa trong vật lý của vũ trụ sơ khai, trước cả giai đoạn lạm phát và gần với mô hình vũ trụ học tiên đoán tồn tại kỳ dị của Vụ Nổ Lớn. Câu trả lời cho trạng thái của giai đoạn sơ khai này đòi hỏi các nhà vật lý phát triển một lý thuyết hoàn thiện về hấp dẫn lượng tử, mà vẫn chưa có được[143] (xem phần Hấp dẫn lượng tử bên dưới).
Các khái niệm mở rộng[sửa | sửa mã nguồn]
Cấu trúc nhân quả và hình học toàn cục[sửa | sửa mã nguồn]

Trong thuyết tương đối rộng, không vật nào có vận tốc bằng hoặc vượt tốc độ ánh sáng. Không có sự ảnh hưởng nào từ sự kiện A có thể đến vị trí X trước khi ánh sáng gửi từ A đến X (xem thêm phần Chuyển sang tương đối tính ở trên). Hệ quả của nó là bằng cách sử dụng mọi tuyến thế giới của ánh sáng (light worldline-hay đường trắc địa không) chúng ta sẽ thu được thông tin về cấu trúc nhân quả của không thời gian. Cấu trúc này được thể hiện bằng biểu đồ Penrose–Carter trong đó những vùng không gian lớn vô hạn và khoảng thời gian lớn vô hạn được co lại một cách compact hóa để vừa với một biểu đồ nhỏ, trong khi vẫn cho phép ánh sáng chuyển động trên đường nghiêng 45° hoặc 135° như trong các biểu đồ Minkowski.[144]
Nhận thức được vai trò quan trọng của cấu trúc nhân quả, nhà toán học Roger Penrose và những người khác đã phát triển ra hình học toàn cục. Trong hình học này, đối tượng nghiên cứu không phải là một nghiệm đặc biệt (hoặc họ nghiệm) của phương trình Einstein, mà là những liên hệ thỏa mãn cho mọi đường trắc địa, ví dụ như phương trình Raychaudhuri, cũng như những giả thiết không cụ thể về bản chất của vật chất (như được miêu tả thành các điều kiện năng lượng) và sử dụng để suy ra các kết quả tổng quát.[145]
Chân trời[sửa | sửa mã nguồn]
Sử dụng hình học toàn cục, người ta chứng minh được một số không thời gian chứa những mặt biên gọi là chân trời (hay chân trời sự kiện), mặt phân chia một vùng tách khỏi phần còn lại của không thời gian. Ví dụ hay gặp nhất đó là các lỗ đen: nếu khối lượng bị nén vào một vùng không gian đủ nhỏ (như được nêu trong phỏng đoán vòng-hoop conjecture), với bán kính Schwarzschild tương ứng trong nghiệm Schwarzschild[146]), và ánh sáng không thể thoát từ bên trong ra ngoài. Do không có vật nào vượt qua được ánh sáng, mọi vật chất rơi vào trong đều bị giam giữ lại. Tuy mọi vật không thể thoát ra ngoài nhưng việc vượt qua chân trời sự kiện đi vào bên trong lỗ đen là có thể, và chân trời của lỗ đen chỉ là kỳ dị toán học chứ không phải là kỳ dị vật lý thực (cũng xem phần Cơ sở cho mô hình vật lý ở trên).[147]

Những nghiên cứu ban đầu về các nghiệm chính xác của phương trình trường Einstein, nổi bật là nghiệm Schwarzschild đối xứng cầu (thường dùng để miêu tả lỗ đen dừng (đứng yên) và không quay) và nghiệm Kerr đối xứng trục (dùng để miêu tả lỗ đen dừng, quay quanh trục của nó, lỗ đen này có thêm những đặc trưng mới như mặt cầu sản công-ergosphere). Bằng sử dụng hình học toàn cục, các nhà vật lý sau đó đã phát hiện thêm những tính chất tổng quát của lỗ đen. Đó là miêu tả bằng vật lý các lỗ đen chỉ đơn giản cần mười một tham số xác định bao gồm năng lượng (1 tham số), động lượng (3), mômen động lượng (3), vị trí của nó tại thời gian cụ thể (3) và điện tích (1) lỗ đen. Đây chính là phát biểu của định lý về đặc trưng duy nhất của lỗ đen: "các lỗ đen không có tóc", nghĩa là nó không có những đặc điểm khác phân biệt giống như các kiểu tóc ở người. Nó không phụ thuộc vào sự phức tạp về cấu trúc cũng như thành phần, trạng thái của thiên thể trước khi suy sụp hấp dẫn hình thành lên lỗ đen, lỗ đen sinh ra (sau khi quá trình suy sụp phát ra sóng hấp dẫn) có những đặc điểm rất đơn giản.[148]
Đáng chú ý hơn nữa, có một bộ các định luật gọi là cơ học lỗ đen, tương tự như các định luật nhiệt động lực học. Ví dụ, định luật hai của cơ học lỗ đen, diện tích của chân trời sự kiện của lỗ đen tổng quát sẽ không bao giờ giảm theo thời gian, tương tự như entropy của hệ nhiệt động lực học. Định luật này giới hạn năng lượng mà chúng ta có thể thu được theo nghĩa cổ điển từ một lỗ đen quay (ví dụ theo tiến trình Penrose).[149] Có chứng cứ mạnh cho rằng các định luật của cơ học lỗ đen thực tế chỉ là tập con của các định luật nhiệt động lực học, và diện tích chân trời sự kiện tỷ lệ với entropy của nó.[150] Kết quả này dẫn đến sự sửa đổi các định luật cơ học lỗ đen ban đầu: như định luật thứ hai sẽ trở thành một phần của định luật thứ hai trong nhiệt động lực học, diện tích chân trời lỗ đen không thể giảm—trong khoảng thời gian những quá trình khác đảm bảo rằng, trên toàn thể entropy luôn tăng. Khi xét trên phương diện là một vật trong cân bằng nhiệt động với nhiệt độ khác không, lỗ đen sẽ phát ra bức xạ nhiệt. Những tính toán bán cổ điển cho thấy kết quả đúng như vậy, với bề mặt hấp dẫn đóng vai trò là nhiệt độ trong định luật Planck. Bức xạ này gọi là bức xạ Hawking (xem phần lý thuyết lượng tử bên dưới).[151]
Ngoài chân trời sự kiện ở các lỗ đen còn có những loại chân trời khác. Trong mô hình vũ trụ đang giãn nở, một quan sát viên sẽ thấy rằng một số vùng không thời gian trong quá khứ không bao giờ quan sát được ("chân trời hạt"), và một số vùng trong tương lai không bao giờ bị ảnh hưởng (chân trời vũ trụ học).[152] Ngay cả trong không thời gian Minkowski phẳng, được miêu tả bằng một quan sát viên đang chuyển động gia tốc đều (không gian Rindler), sẽ có chân trời xuất hiện kết hợp với dạng bức xạ bán cổ điển gọi là "hiệu ứng Unruh".[153]
Kỳ dị[sửa | sửa mã nguồn]
Một đặc trưng tổng quát khác—và khá nhiễu loạn—của thuyết tương đối tổng quát đó là sự xuất hiện của những kỳ dị không thời gian. Chúng ta có thể miêu tả cấu trúc không thời gian bằng sử dụng các đường trắc địa kiểu thời gian cũng như các đường truyền tia sáng— mọi con đường khả dĩ mà ánh sáng hay vật chất có thể di chuyển được. Nhưng một số nghiệm của phương trình trường Einstein có những "mỏm sắc"—những vùng gọi là kỳ dị không thời gian, nơi đường trắc địa của ánh sáng và hạt kết thúc đột ngột, và hình học của không thời gian không còn được xác định. Trong trường hợp thú vị hơn, có những "kỳ dị độ cong", nơi các đại lượng đặc trưng bởi độ cong không thời gian, như độ cong vô hướng Ricci hoặc bình phương độ cong Riemann, nhận giá trị vô hạn.[154] Những ví dụ thường gặp về không thời gian với kỳ dị tương lai—nơi tuyến thế giới kết thúc (worldline)—là nghiệm Schwarzschild, miêu tả điểm kỳ dị bên trong lỗ đen dừng không quay (xem Cơ sở cho mô hình vật lý ở trên),[155] hoặc nghiệm Kerr miêu tả vòng kỳ dị bên trong một lỗ đen dừng quay quanh trục của nó.[156] Nghiệm Friedmann–Lemaître–Robertson–Walker và những không thời gian khác miêu tả vũ trụ có điểm kỳ dị quá khứ nơi các tuyến thế giới bắt đầu, hay ở kỳ dị của Vụ Nổ Lớn, cũng như chúng có những điểm kỳ dị tương lai (như Vụ co lớn).[157]
Những nghiệm miêu tả ở trên có một số đặc điểm đối xứng—và do vậy đã được đơn giản hóa—và biết đâu sự xuất hiện của những kỳ dị này chỉ là sự lý tưởng hóa nhân tạo (do giả sử tính đối xứng và chọn hệ tọa độ-xem mục Chân trời ở trên).[158] Tuy nhiên theo định lý điểm kỳ dị, chứng minh bằng phương pháp của hình học toàn cục, nói rằng: các điểm kỳ dị là những đặc điểm chung nội tại của thuyết tương đối tổng quát, và sự suy sụp hấp dẫn của ngôi sao thực với khối lượng đủ lớn trở thành lỗ đen không tránh khỏi xuất hiện điểm kỳ dị này[159] cũng như tồn tại điểm kỳ dị ở sự khởi đầu của những mô hình vũ trụ đang giãn nở.[160] Tuy vậy, định lý này nói rất ít về đặc điểm của các kỳ dị, và hiện nay đang có những nỗ lực nghiên cứu nhằm phân loại cấu trúc những thực thể này (như phỏng đoán BKL).[161] "Phỏng đoán sự kiểm duyệt vũ trụ" phát biểu rằng mọi kỳ dị tương lai thực (cấu hình vật chất không có đối xứng hoàn hảo, cũng như các đặc tính thực khác) bị ẩn giấu an toàn bên dưới chân trời sự kiện, và do vậy quan sát viên ở xa sẽ không nhìn thấy được. Tuy chưa có chứng minh chặt chẽ bằng toán học, các mô phỏng máy tính đều ủng hộ kết quả của phỏng đoán này.[162]
Phương trình tiến hóa[sửa | sửa mã nguồn]
Mỗi nghiệm của phương trình Einstein chứa toàn bộ lịch sử của một không thời gian mà nó miêu tả — nó không chỉ chụp lại vật thể hoạt động như thế nào mà còn là toàn bộ không thời gian có thể chứa vật chất. Nghiệm miêu tả trạng thái của vật chất và hình học khắp nơi và tại mỗi thời điểm trong không thời gian. Do tuân theo nguyên lý hiệp biến tổng quát (tính bất biến của phương trình các định luật vật lý dưới mọi phép biến đổi hệ tọa độ), lý thuyết của Einstein không đủ để xác định phương trình tiến hóa theo thời gian của tenxơ mêtric. Nó phải kết hợp với các điều kiện tọa độ, tương tự như phép trộn chuẩn (gauge fixing) trong những lý thuyết trường khác.[163]
Để hiểu phương trình trường Einstein như là hệ phương trình vi phân riêng phần, sẽ thuận lợi khi chúng ta thiết lập chúng theo cách miêu tả sự tiến hóa của cấu trúc hình học theo thời gian. Điều này được thực hiện trong hình thức "3+1", với không thời gian tách ra thành 3 chiều không gian và 1 chiều thời gian. Ví dụ như hình thức luận ADM.[164] Cách phân tách này cho thấy các phương trình tiến hóa của không thời gian trong thuyết tương đối rộng hoạt động trơn tru: phương trình luôn luôn tồn tại nghiệm xác định duy nhất, và phù hợp với điều kiện ban đầu định trước.[165] Những hình thức luận phân tách phương trình Einstein là cơ sở cho ngành mô phỏng không thời gian trong thuyết tương đối trên siêu máy tính.[166]
Các đại lượng toàn cục và giả cục bộ[sửa | sửa mã nguồn]
Khái niệm phương trình tiến hóa có liên hệ mật thiết với những khía cạnh khác của vật lý tương đối tính tổng quát. Trong lý thuyết Einstein, chúng ta không thể có được một định nghĩa chung cho một thuộc tính có vẻ đơn giản của một hệ như tổng khối lượng (hay năng lượng). Lý do chính đó là trường hấp dẫn—như những trường vật lý khác— phải được gán cho một lượng năng lượng xác định, nhưng các nhà vật lý đã chứng minh rằng về cơ bản chúng ta không thể cục bộ hóa (hay định xứ) năng lượng hấp dẫn (tức là không xác định cụ thể được năng lượng hấp dẫn ở phạm vi cục bộ).[167]
Mặc dù vậy, chúng ta vẫn có thể xác định tổng khối lượng của hệ (khối lượng toàn cục), hoặc sử dụng kỹ thuật "quan sát viên ở xa vô tận" (khối lượng ADM)[168] hoặc các đối xứng phù hợp (khối lượng Komar).[169] Nếu chúng ta trừ vào tổng khối lượng của hệ bởi năng lượng do sóng hấp dẫn mang ra xa vô tận, kết quả thu được gọi là khối lượng Bondi đối với quan sát viên ở xa vô tận.[170] Cũng giống như trong vật lý cổ điển, các nhà vật lý đã chứng minh được những khối lượng này phải dương.[171] Và cũng có tương ứng định nghĩa khối lượng (năng lượng) toàn cục với việc định nghĩa động lượng và mômen động lượng trên toàn cục.[172] Cũng đã có những cố gắng cho việc định nghĩa những đại lượng giả cục bộ, như khối lượng của một hệ cô lập bằng cách chỉ sử dụng những đại lượng được xác định bên trong phạm vi của không thời gian chứa hệ đó. Mục đích của việc này là nhằm thu được những đại lượng giả cục bộ có ích trong việc miêu tả hệ cô lập, như việc phát biểu chính xác bằng toán học phỏng đoán vòng (hoop conjecture).[173]
Mối quan hệ với thuyết lượng tử[sửa | sửa mã nguồn]
Thuyết tương đối tổng quát là một trong hai trụ cột của vật lý hiện đại, trụ cột kia chính là thuyết lượng tử, cơ sở cho hiểu biết của chúng ta về vật chất từ các hạt cơ bản đến vật lý trạng thái rắn.[174] Tuy nhiên, câu hỏi mở về mối liên hệ giữa hai lý thuyết vẫn là bài toán khó của vật lý hiện đại.
Lý thuyết trường lượng tử trong không thời gian cong[sửa | sửa mã nguồn]
Lý thuyết trường lượng tử thông thường, cơ sở của vật lý hạt cơ bản, được xác định trong không thời gian Minkowski phẳng; lý thuyết này miêu tả hành trạng của các hạt vi mô trong trường hấp dẫn rất yếu và coi như bỏ qua giống như thường gặp trên Trái Đất.[175] Để miêu tả những lúc hấp dẫn trở lên đủ mạnh để ảnh hưởng tới vật chất lượng tử, nhưng chưa đủ mạnh để cần thiết phải lượng tử hóa hấp dẫn, các nhà vật lý phải thiết lập lý thuyết trường lượng tử trong không thời gian cong. Những lý thuyết này dựa trên thuyết tương rộng miêu tả bối cảnh không thời gian cong, trên đó xác định một trường lượng tử nhằm miêu tả hành trạng của vật chất lượng tử trong không thời gian đó.[176] Sử dụng lý thuyết này, Hawking và các nhà vật lý chứng minh được lỗ đen phát ra dạng phổ bức xạ vật đen các hạt lượng tử gọi là bức xạ Hawking, dẫn đến hệ quả của sự bốc hơi lỗ đen trong thời gian dài.[177] Như đã miêu tả ngắn ở trên, bức xạ này đóng vai trò quan trọng trong nhiệt động lực học lỗ đen.[178]
Hấp dẫn lượng tử[sửa | sửa mã nguồn]
Sự đòi hỏi cho tính nhất quán giữa cách miêu tả lượng tử về vật chất và miêu tả hình học cấu trúc không thời gian,[179] cũng như sự xuất hiện của kỳ dị không thời gian (nơi độ cong hình học ở thang vi mô), ám chỉ cần thiết có một lý thuyết đầy đủ về hấp dẫn lượng tử: để miêu tả đặc điểm gần kỳ dị bên trong lỗ đen, và ở thời điểm sơ khai của vũ trụ, lý thuyết đòi hỏi hấp dẫn và cấu trúc không thời gian đi kèm được miêu tả bằng ngôn ngữ của vật lý lượng tử.[180] Cho dù đã có những nỗ lực lớn, chưa một lý thuyết hoàn chỉnh và nhất quán nào về hấp dẫn lượng tử hiện nay được công nhận rộng rãi, ngay cả khi hứa hẹn một số ứng cử viên đầy sáng giá.[181]

Khi các nhà vật lý cố gắng tổng quát hóa những lý thuyết trường lượng tử thông thường, và sử dụng vật lý hạt cơ bản để miêu tả các tương tác cơ bản cũng như gộp cả tương tác hấp dẫn vào đã dẫn đến những vấn đề nghiêm trọng. Ở mức năng lượng thấp, cách tiếp cận này đã thành công, với kết quả là lý thuyết trường hữu hiệu (lượng tử) về hấp dẫn được mọi người chấp nhận.[182] Tuy nhiên đối với mức năng lượng cao, kết quả của mô hình mất đi tính tiên đoán của nó ("không tái chuẩn hóa được").[183]

Một lý thuyết nhằm vượt qua những trở ngại này là lý thuyết dây, lý thuyết lượng tử không coi các hạt điểm là những viên gạch cơ bản, mà thay vào đó là những dây dao động rất nhỏ và có một chiều.[184] Lý thuyết này hứa hẹn một cách miêu tả thống nhất cho mọi hạt và các tương tác, bao gồm cả hấp dẫn;[185] nhưng cái giá phải trả là những đặc điểm kì lạ trong lý thuyết dây như không gian có thêm 6 chiều phụ thêm ngoài 3 chiều đã có.[186] Trong giai đoạn mà các nhà lý thuyết dây gọi là "cuộc cách mạng siêu dây lần hai", người ta đã nêu ra phỏng đoán sự kết hợp lý thuyết dây và sự thống nhất với thuyết tương đối tổng quát và siêu đối xứng thành một lý thuyết gọi là siêu hấp dẫn[187] tạo nên một phần của mô hình giả thuyết với 10 chiều không gian và 1 chiều thời gian gọi là thuyết M, một lý thuyết xác định duy nhất và nhất quán về hấp dẫn lượng tử. Tất cả các lý thuyết này đều chưa được thực nghiệm kiểm chứng.[188]
Một cách tiếp cận khác đó là thủ tục lượng tử hóa chính tắc trong cơ học lượng tử. Sử dụng hình thức luận về giá trị ban đầu của thuyết tương đối rộng (xem Phương trình tiến hóa ở trên), các nhà vật lý thu được phương trình Wheeler–deWitt (phương trình tương tụ như phương trình Schrödinger) nhưng đáng tiếc là nó đã không đúng.[189] Tuy thế, với biến Ashtekar được đưa ra,[190] dẫn đến một mô hình hứa hẹn khác đó là hấp dẫn lượng tử vòng. Trong thuyết này, không gian được miêu tả bằng cấu trúc lưới như mạng lưới spin, và nó tiến hóa trong thời gian theo những bước rời rạc.[191]
Phụ thuộc vào đặc điểm nào của thuyết tương đối tổng quát và thuyết lượng tử được giữ nguyên, và mức độ thay đổi các đặc điểm khác,[192] đã có rất nhiều lý thuyết được đưa ra nhằm cạnh tranh với thuyết hấp dẫn lượng tử, như động lực học tam phân,[193] tập nhân quả,[194] mô hình twistor[195] hoặc mô hình dựa trên tích phân đường về vũ trụ lượng tử.[196]
Mọi lý thuyết miêu tả trong phần này vẫn có những vấn đề trong lý luận, khái niệm và phỏng đoán mà chưa vượt qua được. Và chúng đối mặt với chung một vấn đề đó là, chưa có một cách nào nhằm đưa các kết quả lý thuyết ra kiểm chứng bằng thực nghiệm được (và do vậy cho phép các nhà vật lý quyết định được lý thuyết nào có triển vọng trở lên đúng và loại bỏ những lý thuyết nào), mặc dù có hy vọng trong tương lai điều này sẽ thay đổi khi các dữ liệu thực nghiệm trong vật lý hạt cơ bản năng lượng cao cũng như từ các quan sát thiên văn học cho phép với độ chính xác cao hơn và tinh tế hơn.[197]
Trạng thái phát triển[sửa | sửa mã nguồn]

Thuyết tương đối rộng đã nổi lên như là một mô hình thành công lớn về lực hút hấp dẫn và vũ trụ học, mà nó đã vượt qua được rất nhiều quan sát và thí nghiệm kiểm chứng một cách mạch lạc. Tuy nhiên, có những dấu hiệu cho thấy lý thuyết chưa hoàn chỉnh.[198] Vấn đề về hấp dẫn lượng tử và câu hỏi về tính thực tại của các kỳ dị không thời gian vẫn đang là những câu hỏi mở mang tính thời sự.[199] Dữ liệu quan sát mang lại chứng cứ cho năng lượng tối và vật chất tối cho thấy các nhà vật lý cần phải tìm kiếm một nền vật lý mới.[200] Ngay cả với bản thân lý thuyết, thuyết tương đối tổng quát là mỏ vàng giàu tiềm năng cho những khám phá mới. Nhiều nhà vật lý tương đối tính nghiên cứu thuyết tương đối bằng công cụ toán học nhằm tìm hiểu bản chất của các kỳ dị và những tính chất cơ bản của phương trình trường Einstein,[201] cũng như gia tăng sử dụng siêu máy tính để mô phỏng (như miêu tả quá trình các lỗ đen va chạm và sáp nhập) trong lĩnh vực số hóa thuyết tương đối (numerical relativity).[202] Sau sự kiện quan sát được trực tiếp sóng hấp dẫn bởi Advanced LIGO, lĩnh vực thiên văn sóng hấp dẫn đã mở ra một nhánh ứng dụng mới cho thuyết tương đối tổng quát.[79][203][204] Một thế kỷ sau khi được công bố, thuyết tương đối rộng vẫn đang là lĩnh vực nghiên cứu sôi nổi và đầy hứa hẹn trong nhiều thập kỷ tới.[205]
Xem thêm[sửa | sửa mã nguồn]
Chú thích[sửa | sửa mã nguồn]
- ^ “GW150914: LIGO Detects Gravitational Waves”. Black-holes.org. Truy cập ngày 24 tháng 4 năm 2016.
- ^ “Nobel Prize Biography”. Nobel Prize Biography. Nobel Foundation. Truy cập 25 tháng 2 năm 2011.
- ^ Pais 1982, ch. 9 đến 15, Janssen 2005; tập hợp những bài báo cập nhật và những nghiên cứu hiện nay, bao gồm cả các bài báo gốc có trong Renn 2007; bài đánh giá có trong Renn 2005, tr. 110ff. Những bài viết sớm nhất của Einstein gồm Einstein 1907, và Pais 1982, ch. 9. Bài báo quan trọng ông miêu tả phương trình trường của mình trong Einstein 1915, và Pais 1982, ch. 11–15
- ^ Schwarzschild 1916a, Schwarzschild 1916b và Reissner 1916 (sau được bổ sung trong Nordström 1918)
- ^ “"Scientific Background on the Nobel Prize in Physics 2011. The accelerating universe."” (PDF). Nobelprize.org. tr. 2. Truy cập 12 tháng 10 năm 2011..
- ^ Einstein 1917, và Pais 1982, ch. 15e
- ^ Bài báo gốc của Hubble Hubble 1929; bản điện tử đánh giá của Singh 2004, ch. 2–4
- ^ Như báo cáo trong Gamow 1970. Einstein bác bỏ hằng số vũ trụ học là quá sớm, ông đã không suy nghĩ cẩn thận hơn về hằng số này, xem Vũ trụ học bên dưới
- ^ Trong Pais 1982, tr. 253–254
- ^ Kennefick 2005, Kennefick 2007
- ^ Pais 1982, ch. 16
- ^ Thorne, Kip (2003). “Warping spacetime”. The future of theoretical physics and cosmology: celebrating Stephen Hawking's 60th birthday. Cambridge University Press. tr. 74. ISBN 0-521-82081-2., Extract of page 74
- ^ Israel 1987, ch. 7.8–7.10, Thorne 1994, ch. 3–9
- ^ Phần Hiệu ứng quỹ đạo và tính tương đối của phương hướng, Sự giãn thời gian do hấp dẫn và dịch chuyển tần số và Ánh sáng bị lệch và trễ thời gian do hấp dẫn, và những tham khảo trong từng phần.
- ^ Phần Vũ trụ học và tham khảo trong phần này; lịch sử phát minh ra lý thuyết được thảo luận trong Overbye 1999
- ^ Những mô tả dưới đây theo như các lập luận của Ehlers 1973, ph. 1
- ^ Arnold 1989, ch 1
- ^ Ehlers 1973, tr. 5f
- ^ Will 1993, ph 2.4, Will 2006, ph 2
- ^ Wheeler 1990, ch 2
- ^ Ehlers 1973, ph. 1.2, Havas 1964, Künzle 1972. Thí nghiệm tưởng tưọng đơn giản miêu tả đầu tiên trong Heckmann & Schücking 1959
- ^ Ehlers 1973, tr. 10f
- ^ Những sách giới thiệu tăng dần theo độ khó và sử dụng kiến thức toán học gồm Giulini 2005, Mermin 2005, và Rindler 1991; đối với các thí nghiệm chính xác, xem phần IV của Ehlers & Lämmerzahl 2006
- ^ So sánh chi tiết giữa hai nhóm đối xứng miêu tả trong Giulini 2006a
- ^ Rindler 1991, ph. 22, Synge 1972, ch. 1 và 2
- ^ Ehlers 1973, ph. 2.3
- ^ Ehlers 1973, ph. 1.4, Schutz 1985, ph. 5.1
- ^ Ehlers 1973, tr. 17ff; phương pháp suy luận có thể xem trong Mermin 2005, ch 12. Về kết quả thực nghiệm, xem phần Sự giãn thời gian do hấp dẫn và dịch chuyển tần số bên dưới
- ^ Xem Rindler 2001, ph 1.13; đối với cách miêu tả đại chúng xem Wheeler 1990, ch 2; cũng có sự khác nhau giữa phiên bản hiện đại của nguyên lý và khái niệm ban đầu mà Einstein đã sử dụng khi tìm kiếm lý thuyết rộng, xem Norton 1985
- ^ Xem Ehlers 1973, ph. 1.4 về các kết quả thí nghiệm, cũng như xem thêm phần Sự giãn thời gian do hấp dẫn và dịch chuyển tần số. Nếu chúng ta chọn một liên thông khác mà tenxơ độ xoắn khác không (hay hệ quy chiếu quán tính cục bộ được phép quay) thì chúng ta có một lý thuyết sửa đổi khác là lý thuyết Einstein–Cartan
- ^ Misner, Thorne & Wheeler 1973, § 8 và 13
- ^ Ehlers 1973, tr. 16, Kenyon 1990, ph. 7.2, Weinberg 1972, ph. 2.8
- ^ Ehlers 1973, tr. 19–22; đối với nội dung suy ra phương trình trường, xem phần 1 và 2 của ch. 7 trong Weinberg 1972. Trong đa tạp không thời gian bốn chiều, tenxơ Einstein là tenxơ duy nhất thỏa mãn phân kỳ tự do với nó là hàm tổ hợp của tenxơ mêtric, cũng như đạo hàm riêng bậc nhất và bậc hai của tenxơ mêtric, do vậy cho phép không thời gian của thuyết tương đối hẹp như là một nghiệm của phương trình trường khi không có nguồn hấp dẫn, xem Lovelock 1972. Tenxơ ở cả hai vế là tenxơ hạng hai, do đó chúng có thể được biểu diễn bằng ma trận 4×4, mỗi ma trận chứa mười thành phần độc lập; và do đó phương trình trường Einstein là hệ có 10 phương trình. Cụ thể hơn nữa, theo hệ quả của mối liên hệ hình học là đồng nhất thức Bianchi, tenxơ Einstein tự thỏa mãn bốn đồng nhất thức này và do đó giảm số phương trình độc lập của phương trình trường xuống còn sáu, xem Schutz 1985, ph. 8.3
- ^ Kenyon 1990, ph. 7.4
- ^ Tham khảo tương ứng trong Brans & Dicke 1961, Weinberg 1972, ph. 3 trong ch. 7, Goenner 2004, ph. 7.2, và Trautman 2006.
- ^ Wald 1984, ch. 4, Weinberg 1972, ch. 7 hoặc ở các cuốn sách khác về thuyết tương đối tổng quát
- ^ Tổng quan xem trong Poisson 2004
- ^ Wheeler 1990, tr. xi
- ^ Wald 1984, sec. 4.4
- ^ Wald 1984, ph. 4.1
- ^ Về sự khó khăn (khái niệm và lịch sử) trong xác định nguyên lý tương đối tổng quát và phân biệt nó với nguyên lý hiệp biến tổng quát, xem Giulini 2006b
- ^ phần 5 trong ch. 12 của Weinberg 1972
- ^ Chương giới thiệu trong Stephani và đồng nghiệp 2003
- ^ Bài báo tổng quan về phương trình Einstein theo bối cảnh rộng hơn ở các phương trình đạo hàm riêng với ý nghĩa vật lý là Geroch 1996
- ^ Thông tin khái quát và danh sách các nghiệm xem Stephani và đồng nghiệp 2003; bài viết đánh giá gần đây về nghiệm phương trình Einstein là MacCallum 2006
- ^ Chandrasekhar 1983, ch. 3,5,6
- ^ Narlikar 1993, ch. 4, ph. 3.3
- ^ Giới thiệu ngắn về những nghiệm này và những nghiệm khác được trình bày trong Hawking & Ellis 1973, ch. 5
- ^ Lehner 2002
- ^ Xem Wald 1984, ph. 4.4
- ^ Will 1993, ph. 4.1 và 4.2
- ^ Will 2006, ph. 3.2, Will 1993, ch. 4
- ^ Misner, Thorne & Wheeler 1973, § 23.1
- ^ Misner, Thorne & Wheeler 1973, § 23
- ^ Rindler 2001, tr. 24–26 và pp. 236–237 và Ohanian & Ruffini 1994, tr. 164–172. Einstein suy luận ra hiệu ứng này nhờ sử dụng nguyên lý tương đương vào đầu năm 1907, xem Einstein 1907 và quá trình tìm kiến thuyết tương đối rộng trong Pais 1982, tr. 196–198
- ^ Rindler 2001, tr. 24–26; Misner, Thorne & Wheeler 1973, § 38.5
- ^ Thí nghiệm Pound-Rebka, xem Pound & Rebka 1959, Pound & Rebka 1960; Pound & Snider 1964; danh sách đầy đủ các thí nghiệm có trong Ohanian & Ruffini 1994, bảng 4.1 ở tr. 186
- ^ Greenstein, Oke & Shipman 1971; đo đạc gần đây và chính xác nhất đối với sao Sirius B công bố trong Barstow, Bond et al. 2005.
- ^ Đầu tiên là thí nghiệm Hafele-Keating, Hafele & Keating 1972a và Hafele & Keating 1972b, đến thí nghiệm trên vệ tinh Gravity Probe A; khái quát về các thí nghiệm này có trong Ohanian & Ruffini 1994, bảng 4.1 ở tr. 186
- ^ Thời gian trên hệ GPS liên tục được so sánh giữa đồng hồ nguyên tử đặt trên vệ tinh và dưới mặt đất; thảo luận về những hiệu ứng tương đối tính có trong Ashby 2002 và Ashby 2003
- ^ Stairs 2003 và Kramer 2004
- ^ Xem tổng hợp trong ph 2.1. của Will 2006; Will 2003, tr. 32–36; Ohanian & Ruffini 1994, ph. 4.2
- ^ Ohanian & Ruffini 1994, tr. 164–172
- ^ Xem Kennefick 2005 cho những đo đạc đầu tiên của đoàn thám hiểm Eddington; về kết quả của những đo lường gần đây, xem Ohanian & Ruffini 1994, ch. 4.3. Đối với những quan sát hiện đại chính xác nhất sử dụng quasars xem Shapiro và đồng nghiệp 2004
- ^ Đây không phải là một tiên đề độc lập; tính bất biến này có thể suy ra từ phương trình trường Einstein và Lagrangian cho phương trình Maxwell sử dụng xấp xỉ WKB, xem Ehlers 1973, ph. 5
- ^ Blanchet 2006, ph. 1.3
- ^ Trong Rindler 2001, ph. 1.16; đối với ví dụ lịch sử Israel 1987, tr. 202–204; thực ra Einstein đã phát hiện sự lệch ánh sáng truyền qua thang máy rơi tự do trong Einstein 1907 nhưng giá trị ông thu được ban đầu chỉ bằng một nửa giá trị khi ông đã tìm ra được phương trình trường năm 1915. Một số tính toán giả sử không thời gian là không gian Euclid có trong Ehlers & Rindler 1997
- ^ Xét về bản chất theo lý thuyết tương đối tổng quát Einstein, những tính toán độ lệch ánh sáng dựa vào sự rơi tự do chỉ tính đến ảnh hưởng của hấp dẫn lên thời gian, mà không tính đến ảnh hưởng của hấp dẫn làm cong không gian, xem Rindler 2001, ph. 11.11
- ^ Đối với trường hấp dẫn Mặt Trời sử dụng tính hiệu rada phản xạ từ các hành tinh như Sao Kim và Sao Thủy xem Shapiro 1964, Weinberg 1972, ch. 8, ph. 7; đối với các tín hiệu chủ động phản hồi từ các tàu không gian (đo phát đáp tín hiệu) xem Bertotti, Iess & Tortora 2003; đánh giá tổng quan xem Ohanian & Ruffini 1994, table 4.4 ở tr. 200; đối với những phép đo gần đây sử dụng tín hiệu từ các pulsar trong hệ đôi, trường hấp dẫn từ một pulsar đồng hành làm trễ thời gian truyền tín hiệu từ pulsar kia xem Stairs 2003, ph. 4.4
- ^ Will 1993, ph. 7.1 và 7.2
- ^ Đã có quan sát gián tiếp xác nhận sự tồn tại của sóng hấp dẫn thông qua sự mất mát năng lượng trong hệ pulsar đôi như hệ pulsar Hulse–Taylor, mà nhờ các quan sát này mà hai ông đã nhận giải Nobel Vật lý năm 1993. Hiện nay đang có nhiều dự án nhằm đo được trực tiếp hiệu ứng của sóng hấp dẫn. Về thực nghiệm sóng hấp dẫn xem Misner, Thorne & Wheeler 1973, part VIII. Không giống như sóng điện từ, đóng góp chủ yếu của sóng hấp dẫn không phải là lưỡng cực, mà là tứ cực; xem Schutz 2001
- ^ Hầu hết các sách viết về thuyết tương đối rộng nâng cao đều có chương miêu tả phương pháp suy luận cũng như tính chất của sóng hấp dẫn, ví dụ xem Schutz 1985, ch. 9
- ^ Xem trong Jaranowski & Królak 2005
- ^ Rindler 2001, ch. 13
- ^ Gowdy 1971, Gowdy 1974
- ^ Xem Lehner 2002 với giới thiệu ngắn về phương pháp mô phỏng số thuyết tương đối rộng, và Seidel 1998 cho sự liên hệ với thiên văn quan sát sóng hấp dẫn.
- ^ a b Castelvecchi, Davide; Witze, Witze (ngày 11 tháng 2 năm 2016). “Einstein's gravitational waves found at last”. Nature News. doi:10.1038/nature.2016.19361. Truy cập ngày 11 tháng 2 năm 2016.
- ^ a b B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016). “Observation of Gravitational Waves from a Binary Black Hole Merger”. Physical Review Letters. 116 (6). doi:10.1103/PhysRevLett.116.061102.Quản lý CS1: sử dụng tham số tác giả (liên kết)
- ^ a b “Gravitational waves detected 100 years after Einstein's prediction | NSF - National Science Foundation”. www.nsf.gov. Truy cập ngày 11 tháng 2 năm 2016.
- ^ Schutz 2003, tr. 48–49, Pais 1982, tr. 253–254
- ^ Rindler 2001, ph. 11.9
- ^ Will 1993, tr. 177–181
- ^ Hệ quả là, trong hình thức tham số hóa hậu Newton (PPN), các đo đạc về hiệu ứng này xác định lên giá trị tổ hợp tuyến tính của hai số hạng β và γ xem Will 2006, ph. 3.5 và Will 1993, ph. 7.3
- ^ Những đo lường chính xác nhất sử dụng phương pháp giao thoa kế vô tuyến đường cơ sở dài cho vị trí các hành tinh; xem Will 1993, ch. 5, Will 2006, ph. 3.5, Anderson và đồng nghiệp 1992; tổng quan xem Ohanian & Ruffini 1994, tr. 406–407
- ^ Kramer và đồng nghiệp 2006
- ^ Một biểu đồ thể hiện sai số đo đạc nằm ở hình 7 trong Will 2006, ph. 5.1
- ^ Stairs 2003, Schutz 2003, tr. 317–321, Bartusiak 2000, tr. 70–86
- ^ Trong Weisberg & Taylor 2003, liên quan đến lịch sử khám phá xem Hulse & Taylor 1975, về mô tả ban đầu của hiệu ứng suy giảm chu kỳ quỹ đạo xem Taylor 1994
- ^ Kramer 2004
- ^ Penrose 2004, §14.5, Misner, Thorne & Wheeler 1973, §11.4
- ^ Weinberg 1972, ph. 9.6, Ohanian & Ruffini 1994, ph. 7.8
- ^ Bertotti, Ciufolini & Bender 1987, Nordtvedt 2003
- ^ Kahn 2007
- ^ a b Mô tả về phi vụ có trong Everitt và đồng nghiệp 2001; kết quả thí nghiệm sơ bộ có trong Everitt, Parkinson & Kahn 2007; những dữ liệu cập nhật tại website Kahn 1996–2012.
- ^ Townsend 1997, ph. 4.2.1, Ohanian & Ruffini 1994, tr. 469–471
- ^ Ohanian & Ruffini 1994, ph. 4.7, Weinberg 1972, ph. 9.7; miêu tả thí nghiệm kiểm tra gần đây trong Schäfer 2004
- ^ Ciufolini & Pavlis 2004, Ciufolini, Pavlis & Peron 2006, Iorio 2009
- ^ Iorio L. (tháng 8 năm 2006), “COMMENTS, REPLIES AND NOTES: A note on the evidence of the gravitomagnetic field of Mars”, Classical Quantum Gravity, 23 (17): 5451–5454, arXiv:gr-qc/0606092, Bibcode:2006CQGra..23.5451I, doi:10.1088/0264-9381/23/17/N01
- ^ Iorio L. (tháng 6 năm 2010), “On the Lense–Thirring test with the Mars Global Surveyor in the gravitational field of Mars”, Central European Journal of Physics, 8 (3): 509–513, arXiv:gr-qc/0701146, Bibcode:2010CEJPh...8..509I, doi:10.2478/s11534-009-0117-6
- ^ Miêu tả về thấu kính hấp dẫn và các ứng dụng của nó có trong Ehlers, Falco & Schneider 1992 và Wambsganss 1998
- ^ Chứng minh bằng toán học xem Schutz 2003, ch. 23; và Narayan & Bartelmann 1997, ph. 3
- ^ Walsh, Carswell & Weymann 1979
- ^ Hình ảnh của tất cả các thấu kính hấp dẫn đã được phát hiện có tại trang của dự án CASTLES, Kochanek và đồng nghiệp 2007
- ^ Roulet & Mollerach 1997
- ^ Narayan & Bartelmann 1997, ph. 3.7
- ^ Barish 2005, Bartusiak 2000, Blair & McNamara 1997
- ^ Hough & Rowan 2000
- ^ Hobbs, George. "The international pulsar timing array project: using pulsars as a gravitational wave detector". arΧiv:0911.5206.
- ^ Danzmann & Rüdiger 2003
- ^ “LISA pathfinder overview”. ESA. Truy cập ngày 23 tháng 4 năm 2013.
- ^ M. Armano; và đồng nghiệp (2016). “Sub-Femto-g Free Fall for Space-Based Gravitational Wave Observatories: LISA Pathfinder Results”. Physical Review Letters. 116 (23). doi:10.1103/PhysRevLett.116.231101.
- ^ “LISA Pathfinder exceeds expectations”. ESA. ngày 7 tháng 6 năm 2016. Truy cập ngày 7 tháng 6 năm 2016.
- ^ “LISA Pathfinder exceeds expectations”. Benjamin Knispel. elisascience.org. ngày 7 tháng 6 năm 2016. Bản gốc lưu trữ ngày 3 tháng 8 năm 2016. Truy cập ngày 7 tháng 6 năm 2016.
- ^ Thorne 1995
- ^ Cutler & Thorne 2002
- ^ Miller 2002, bài giảng 19 và 21
- ^ Celotti, Miller & Sciama 1999, ph. 3
- ^ Springel và đồng nghiệp 2005 và Gnedin 2005
- ^ Blandford 1987, ph. 8.2.4
- ^ Về cơ chế cơ bản, xem Carroll & Ostlie 1996, ph. 17.2; về những loại thiên thể khác nhau có liên quan đến quá trình bồi tụ xem Robson 1996
- ^ Xem Begelman, Blandford & Rees 1984. Đối với một quan sát viên ở xa, đôi khi chùm tia này hiện lên như chuyển động nhanh hơn ánh sáng; và điều này đã được giải thích như là một ảo ảnh quang học mà không vi phạm thuyết tương đối, xem Rees 1966
- ^ Đối với trạng thái tiến hóa cuối cùng của ngôi sao xem Oppenheimer & Snyder 1939 và cho mô phỏng số Font 2003, ph. 4.1; đối với các siêu tân tinh vẫn còn những vấn đề mở như miêu tả trong Buras và đồng nghiệp 2003; về mô phỏng quá trình bồi tụ và hình thành tia tương đối tính xem Font 2003, ph. 4.2. Cũng vậy, hiệu ứng thấu kính hấp dẫn có vai trò quan trọng trong tín hiệu thu được từ các pulsar phát ra tia X, xem Kraus 1998
- ^ Chứng cứ bao gồm giới hạn về vùng rất nhỏ từ các quan sát hiện tượng bồi tụ, xem Celotti, Miller & Sciama 1999, hoặc các quan sát về chuyển động các ngôi sao xung quanh một vùng rất nhỏ ở trung tâm của Ngân Hà xem Schödel và đồng nghiệp 2003, và hệ quả gián tiếp về quan sát những thiên thể nén đặc, các bùng nổ tia X mà những vật thể ở trung tâm hoặc là sao neutron hoặc là lỗ đen khối lượng sao; xem Remillard và đồng nghiệp 2006 và Narayan 2006, ph. 5. Quan sát chân trời sự kiện của lỗ đen ở trung tâm Ngân Hà cũng đang được tiến hành, xem Falcke, Melia & Agol 2000
- ^ Dalal và đồng nghiệp 2006
- ^ Barack & Cutler 2004
- ^ Nguồn gốc của phương trình trong Einstein 1917; về lịch sử xem Pais 1982, tr. 285–288
- ^ Carroll 2001, ch. 2
- ^ Xem Bergström & Goobar 2003, ch. 9–11; dựa trên thực tế quan sát là ở thang khoảng cách lớn trên 100 Mpc, vũ trụ của chúng ta hiện ra với vật chất và bức xạ phân bố gần như đồng nhất và không theo một hướng ưu tiên nào, đẳng hướng; xem Peebles và đồng nghiệp 1991. Tuy vậy kết quả quan sát gần đây từ tàu Planck cho thấy vũ trụ gần đồng nhất và hơi phi đẳng hướng.
- ^ a b c "Scientific Background on the Nobel Prize in Physics 2011. The accelerating universe." (tr 5) Nobelprize.org.
- ^ Ví dụ với dữ liệu thu được từ tàu WMAP xem Spergel và đồng nghiệp 2003
- ^ Những kiểm tra này bao gồm những chi tiết quan sát độc lập khác, ví dụ xem hình 2 trong Bridle và đồng nghiệp 2003
- ^ Peebles 1966; với những tiên đoán gần đây xem Coc, Vangioni‐Flam et al. 2004; bài viết online của Weiss 2006; so sánh hệ quả lý thuyết với dữ liệu quan sát có trong Olive & Skillman 2004, Bania, Rood & Balser 2002, O'Meara và đồng nghiệp 2001, và Charbonnel & Primas 2005
- ^ Lahav & Suto 2004, Bertschinger 1998, Springel và đồng nghiệp 2005
- ^ Alpher & Herman 1948, giới thiệu đại cương có trong Bergström & Goobar 2003, ch. 11; đối với phát hiện tình cờ ra bức xạ vi sóng, xem Penzias & Wilson 1965, và kết quả đo lường chính xác từ các đài quan sát vệ tinh, Mather và đồng nghiệp 1994 (COBE), Bennett và đồng nghiệp 2003 (WMAP) và kết quả mới nhất từ tàu Planck (2013) tại trang chủ. Những dự án trong tương lai cũng sẽ tiết lộ manh mối về sóng hấp dẫn trong vũ trụ sơ khởi; cung cấp thêm thông tin về sự phân cực của bức xạ nền, xem Kamionkowski, Kosowsky & Stebbins 1997 và Seljak & Zaldarriaga 1997
- ^ Bằng chứng cho vật chất tối được suy ra từ các tham số vũ trụ học và những quan sát từ động lực của các thiên hà, siêu đám thiên hà xem Peebles 1993, ch. 18, thông qua hiện tượng thấu kính hấp dẫn xem Peacock 1999, ph. 4.6, và thông qua mô phỏng cấu trúc lớn vũ trụ xem Springel và đồng nghiệp 2005
- ^ Peacock 1999, ch. 12, Peskin 2007; hơn nữa, các khảo sát cũng chỉ ra rằng đa số vật chất tối không thuộc dạng của các hạt cơ bản đã biết ("vật chất phi-baryon" hay vật chất tối), xem Peacock 1999, ch. 12
- ^ Có nghĩa là, một số nhà vật lý đặt ra câu hỏi liệu vật chất tối có thực sự tồn tại hay lý thuyết tương đối tổng quát của Einstein (và lý thuyết Newton) có một số sai lệch khi miêu tả hấp dẫn trên khoảng cách vũ trụ, xem Mannheim 2006, ph. 9
- ^ Carroll 2001; bài viết tổng quan ở trang web Caldwell 2004. Ở dạng năng lượng này cũng vậy, các nhà khoa học tranh luận rằng chứng cứ này có thể không cần thiết phải đòi hỏi dạng năng lượng tối mà thay vào đó cần một lý thuyết mới về trường hấp dẫn cho mô hình vũ trụ học, xem Mannheim 2006, ph. 10; cũng có những điều chỉnh mà không cần phải thay thế thuyết tương đối tổng quát, ví dụ, các nhà vật lý có thể sử dụng giả thiết sự không đồng nhất và phi đẳng hướng của vật chất trong vũ trụ, xem Buchert 2007
- ^ Giới thiệu đại cương trong Linde 1990; đối với nghiên cứu gần đây xem Linde 2005
- ^ Nguyên lý vũ trụ học chỉ giả thuyết vũ trụ là đồng nhất và đẳng hướng, chứ không nêu tại sao lại như vậy. Chính xác hơn, có những vấn đề bao gồm vấn đề độ phẳng, vấn đề chân trời,và vấn đề đơn cực; giới thiệu khái quát dễ hiểu có trong Narlikar 1993, ph. 6.4, cũng xem Börner 1993, ph. 9.1
- ^ Spergel và đồng nghiệp 2007, ph. 5,6
- ^ Cụ thể hơn, hàm thế năng có vai trò quan trọng trong động lực của sự lạm phát chỉ đơn giản là giả thuyết, chứ nó không được suy ra từ một lý thuyết vật lý nào
- ^ Brandenberger 2007, ph. 2
- ^ Frauendiener 2004, Wald 1984, ph. 11.1, Hawking & Ellis 1973, ph. 6.8, 6.9
- ^ Wald 1984, ph. 9.2–9.4 và Hawking & Ellis 1973, ch. 6
- ^ Thorne 1972; về những mô phỏng số xem Berger 2002, ph. 2.1
- ^ Israel 1987. Phân tích chính xác bằng toán học cho thấy có một số kiểu chân trời, bao gồm chân trời sự kiện và chân trời biểu kiến xem Hawking & Ellis 1973, tr. 312–320 hoặc Wald 1984, ph. 12.2; không có một hình ảnh trực giác nào minh họa chân trời của một hệ cô lập mà không đòi hỏi kiến thức về tính chất của không thời gian ở vị trí vô tận, xem Ashtekar & Krishnan 2004
- ^ Nghiên cứu đầu tiên xem Israel 1971; và xem Hawking & Ellis 1973, ph. 9.3 hoặc Heusler 1996, ch. 9 và 10 về chứng minh toán học, và Heusler 1998 cũng như Beig & Chruściel 2006 về những kết quả nghiên cứu gần đây.
- ^ Các định luật cơ học lỗ đen được miêu tả lần đầu tiên trong Bardeen, Carter & Hawking 1973; miêu tả dễ hiểu hơn có trong Carter 1979; đánh giá kết quả gần đây xem Wald 2001, ch. 2. Cuốn sách trình bày các công cụ toán học cần thiết là Poisson 2004. Về quá trình Penrose, xem Penrose 1969
- ^ Bekenstein 1973, Bekenstein 1974
- ^ Phát hiện ra lỗ đen, trên khuôn khổ cơ học lượng tử, phát ra bức xạ được chứng minh đầu tiên trong Hawking 1975; suy luận chi tiết có trong Wald 1975. Bài viết tổng quan trong Wald 2001, ch. 3
- ^ Narlikar 1993, ph. 4.4.4, 4.4.5
- ^ Về "chân trời": xem Rindler 2001, ph. 12.4. Hiệu ứng Unruh: Unruh 1976, và Wald 2001, ch. 3
- ^ Hawking & Ellis 1973, ph. 8.1, Wald 1984, ph. 9.1
- ^ Townsend 1997, ch. 2; một miêu tả kỹ lưỡng về nghiệm này trong Chandrasekhar 1983, ch. 3
- ^ Townsend 1997, ch. 4; đối với miêu tả chi tiết xem Chandrasekhar 1983, ch. 6
- ^ Ellis & van Elst 1999; một cái nhìn gần hơn về điểm kỳ dị miêu tả trong Börner 1993, ph. 1.2
- ^ Có một chú ý về thực tế quan trọng của hiện tượng kỳ dị giả quang học xuất hiện trong nhiều phương trình sóng, "sự tụ quang", được giải quyết khi cho các kết quả hữu hạn sau khi thay thế phương pháp xấp xỉ.
- ^ Xem Penrose 1965
- ^ Hawking 1966
- ^ Phỏng đoán được phát biểu trong Belinskii, Khalatnikov & Lifschitz 1971; bài viết đánh giá gần đây Berger 2002. Nội dung của nó cũng được trình bày trên trang online Garfinkle 2007
- ^ Sự ẩn giấu của kỳ dị tương lai đối với quan sát viên ở xa có bản chất khác hẳn so với những kỳ dị quá khứ ở vũ trụ sơ khai như kỳ dị vụ nổ lớn, mà về nguyên lý chúng hiện ra dưới kính thiên văn của quan sát viên ở thời điểm sau khi diễn ra vụ nổ. Phỏng đoán sự kiểm duyệt vũ trụ được nêu ra lần đầu trong Penrose 1969; cuốn sách miêu tả về phỏng đoán này bao gồm Wald 1984, tr. 302–305. Về những kết quả mô phỏng trên siêu máy tính xem Berger 2002, ph. 2.1
- ^ Hawking & Ellis 1973, ph. 7.1
- ^ Arnowitt, Deser & Misner 1962; miêu tả dễ hiểu trong Misner, Thorne & Wheeler 1973, §21.4–§21.7
- ^ Fourès-Bruhat 1952 và Bruhat 1962; về giới thiệu một cách mô phạm xem Wald 1984, ch. 10; bản trực tuyến miêu tả phương trình tiến hóa ở Reula 1998
- ^ Gourgoulhon 2007; bài viết miêu tả cơ sở của mô phỏng số thuyết tương đối, bao gồm vấn đề xuất hiện các đặc điểm kỳ lạ của phương trình trường Einstein, xem Lehner 2001
- ^ Misner, Thorne & Wheeler 1973, §20.4
- ^ Arnowitt, Deser & Misner 1962
- ^ Komar 1959; trong giáo trình cho sinh viên cao học Wald 1984, ph. 11.2; mặc dù định nghĩa theo một cách hoàn toàn khác, có thể chứng minh sự tương đương giữa khối lượng Komar và khối lượng ADM trong không thời gian dừng, xem Ashtekar & Magnon-Ashtekar 1979
- ^ Nội dung giới thiệu xem Wald 1984, ph. 11.2
- ^ Wald 1984, tr. 295 và các trang tiếp theo; đây là kết quả quan trọng cho câu hỏi về sự ổn định của hệ—nếu có trạng thái khối lượng âm, thì không gian chân không Minkowski phẳng với khối lượng không có thể hình thành lên từ những trạng thái khối lượng âm này.
- ^ Townsend 1997, ch. 5
- ^ Định nghĩa khối lượng–năng lượng giả cục bộ bao gồm năng lượng Hawking, năng lượng Geroch, hoặc năng lượng-động lượng giả cục bộ Penrose dựa trên phương pháp twistor; xem bài báo Szabados 2004
- ^ Có rất nhiều giáo trình về cơ học lượng tử như Messiah 1999; giáo trình cơ sở như Hey & Walters 2003
- ^ Ramond 1990, Weinberg 1995, Peskin & Schroeder 1995; và Auyang 1995
- ^ Wald 1994, Birrell & Davies 1984
- ^ Về bức xạ Hawking xem Hawking 1975, Wald 1975; miêu tả về lỗ đen bốc hơi trong Traschen 2000
- ^ Wald 2001, ch. 3
- ^ Nói đơn giản, vật chất là nguồn của độ cong không thời gian, và khi vật chất thể hiện đặc tính lượng tử, chúng ta cũng hy vọng rằng không thời gian cũng có tính chất như thế, Carlip 2001, ph. 2
- ^ Schutz 2003, tr. 407
- ^ Niên biểu các lý thuyết đề xuất cho hấp dẫn lượng tử miêu tả trong Rovelli 2000
- ^ Donoghue 1995
- ^ Đặc biệt, khi các nhà vật lý áp dụng kĩ thuật tái chuẩn hóa, hàm tích phân cho phép suy luận kết quả, và khi tính đến hiệu ứng năng lượng cao, trở lên không xác định và sai, xem Weinberg 1996, ch. 17, 18, và Goroff & Sagnotti 1985
- ^ Giáo trình cho sinh viên là Zwiebach 2004; bài viết với độ khó hơn Polchinski 1998a và Polchinski 1998b
- ^ Ở mức năng lượng hiện tại mà các mày gia tốc đạt đến (14 TeV), những dây này không thể phân biệt được với các hạt điểm, nhưng có điểm quan trọng là, các mode dao động khác nhau của cùng một dây cơ bản sẽ hiện ra tương ứng với các hạt khác nhau (về điện tích cũng như các tính chất lượng tử khác), xem Ibanez 2000. Lý thuyết này thành công ở chỗ có một mode dao động của dây tương ứng với hạt lượng tử graviton, hạt giả thuyết truyền tương tác hấp dẫn, xem Green, Schwarz & Witten 1987, ph. 2.3, 5.3
- ^ Green, Schwarz & Witten 1987, ph. 4.2
- ^ Weinberg 2000, ch. 31
- ^ Townsend 1996, Duff 1996
- ^ Kuchař 1973, ph. 3
- ^ những biến này đại diện cho hình học hấp dẫn sử dụng sự tương tự toán học giống với điện trường và từ trường; xem Ashtekar 1986, Ashtekar 1987
- ^ Miêu tả khái quát trong Thiemann 2006; mở rộng hơn có trong Rovelli 1998, Ashtekar & Lewandowski 2004 cũng như bài giảng Thiemann 2003
- ^ Isham 1994, Sorkin 1997
- ^ Loll 1998
- ^ Sorkin 2005
- ^ Penrose 2004, ch. 33 và các chương sau
- ^ Hawking 1987
- ^ Ashtekar 2007, Schwarz 2007
- ^ Maddox 1998, tr. 52–59, 98–122; Penrose 2004, sec. 34.1, ch. 30
- ^ Mục Hấp dẫn lượng tử ở trên.
- ^ Mục Vũ trụ học ở trên.
- ^ Friedrich 2005
- ^ Bài viết tổng quan về nhiều vấn đề và các kỹ thuật được phát triển để vượt qua chúng, xem Lehner 2002
- ^ Xem Bartusiak 2000 về miêu tả thiên văn sóng hấp dẫn trước đó; các tin tức cập nhật có thể tìm tại những trang web của các viện nghiên cứu cộng tác chính như GEO 600 Lưu trữ 2007-02-18 tại Wayback Machine và LIGO
- ^ Đối với các bài báo gần đây về tính phân cực của sóng hấp dẫn hoặc chuyển động xoáy ốc của cặp vật thể đặc chắc, xem Blanchet và đồng nghiệp 2008, và Arun và đồng nghiệp 2007; bài viết đánh giá tổng quan nghiên cứu về cặp vật thể đặc chắc, xem Blanchet 2006 và Futamase & Itoh 2006; bài viết tổng quan về các thí nghiệm và quan sát kiểm chứng thuyết tương đối rộng, xem Will 2006
- ^ Ví dụ, xem tạp chí Living Reviews in Relativity Lưu trữ 2016-12-27 tại Wayback Machine
Nguồn tham khảo[sửa | sửa mã nguồn]
- Alpher, R. A.; Herman, R. C. (1948), “Evolution of the universe”, Nature, 162 (4124): 774–775, Bibcode:1948Natur.162..774A, doi:10.1038/162774b0
- Anderson, J. D.; Campbell, J. K.; Jurgens, R. F.; Lau, E. L. (1992), “Recent developments in solar-system tests of general relativity”, trong Sato, H.; Nakamura, T. (biên tập), Proceedings of the Sixth Marcel Großmann Meeting on General Relativity, World Scientific, tr. 353–355, ISBN 981-02-0950-9
- Arnold, V. I. (1989), Mathematical Methods of Classical Mechanics, Springer, ISBN 3-540-96890-3
- Arnowitt, Richard; Deser, Stanley; Misner, Charles W. (1962), “The dynamics of general relativity”, trong Witten, Louis (biên tập), Gravitation: An Introduction to Current Research, Wiley, tr. 227–265
- Arun, K.G.; Blanchet, L.; Iyer, B. R.; Qusailah, M. S. S. (2007), Inspiralling compact binaries in quasi-elliptical orbits: The complete 3PN energy flux, arXiv:0711.0302, Bibcode:2008PhRvD..77f4035A, doi:10.1103/PhysRevD.77.064035
- Ashby, Neil (2002), “Relativity and the Global Positioning System” (PDF), Physics Today, 55 (5): 41–47, Bibcode:2002PhT....55e..41A, doi:10.1063/1.1485583
- Ashby, Neil (2003), “Relativity in the Global Positioning System”, Living Reviews in Relativity, 6, Bản gốc lưu trữ ngày 4 tháng 7 năm 2007, truy cập ngày 6 tháng 7 năm 2007 Liên kết ngoài trong
|journal=(trợ giúp) - Ashtekar, Abhay (1986), “New variables for classical and quantum gravity”, Phys. Rev. Lett., 57 (18): 2244–2247, Bibcode:1986PhRvL..57.2244A, doi:10.1103/PhysRevLett.57.2244, PMID 10033673
- Ashtekar, Abhay (1987), “New Hamiltonian formulation of general relativity”, Phys. Rev., D36 (6): 1587–1602, Bibcode:1987PhRvD..36.1587A, doi:10.1103/PhysRevD.36.1587
- Ashtekar, Abhay (2007), Loop Quantum Gravity: Four Recent Advances and a Dozen Frequently Asked Questions, arXiv:0705.2222, Bibcode:2008mgm..conf..126A, doi:10.1142/9789812834300_0008
- Ashtekar, Abhay; Krishnan, Badri (2004), “Isolated and Dynamical Horizons and Their Applications”, Living Rev. Relativity, 7, truy cập ngày 5 tháng 4 năm 2015
- Ashtekar, Abhay; Lewandowski, Jerzy (2004), “Background Independent Quantum Gravity: A Status Report”, Class. Quant. Grav., 21 (15): R53–R152, arXiv:gr-qc/0404018, Bibcode:2004CQGra..21R..53A, doi:10.1088/0264-9381/21/15/R01
- Ashtekar, Abhay; Magnon-Ashtekar, Anne (1979), “On conserved quantities in general relativity”, Journal of Mathematical Physics, 20 (5): 793–800, Bibcode:1979JMP....20..793A, doi:10.1063/1.524151
- Auyang, Sunny Y. (1995), How is Quantum Field Theory Possible?, Oxford University Press, ISBN 0-19-509345-3
- Bania, T. M.; Rood, R. T.; Balser, D. S. (2002), “The cosmological density of baryons from observations of 3He+ in the Milky Way”, Nature, 415 (6867): 54–57, Bibcode:2002Natur.415...54B, doi:10.1038/415054a, PMID 11780112
- Barack, Leor; Cutler, Curt (2004), “LISA Capture Sources: Approximate Waveforms, Signal-to-Noise Ratios, and Parameter Estimation Accuracy”, Phys. Rev., D69 (8): 082005, arXiv:gr-qc/0310125v3, Bibcode:2004PhRvD..69h2005B, doi:10.1103/PhysRevD.69.082005
- Bardeen, J. M.; Carter, B.; Hawking, S. W. (1973), “The Four Laws of Black Hole Mechanics”, Comm. Math. Phys., 31 (2): 161–170, Bibcode:1973CMaPh..31..161B, doi:10.1007/BF01645742
- Barish, Barry (2005), “Towards detection of gravitational waves”, trong Florides, P.; Nolan, B.; Ottewil, A. (biên tập), General Relativity and Gravitation. Proceedings of the 17th International Conference, World Scientific, tr. 24–34, ISBN 981-256-424-1
- Barstow, M; Bond, Howard E.; Holberg, J. B.; Burleigh, M. R.; Hubeny, I.; Koester, D. (2005), “Hubble Space Telescope Spectroscopy of the Balmer lines in Sirius B”, Mon. Not. Roy. Astron. Soc., 362 (4): 1134–1142, arXiv:astro-ph/0506600, Bibcode:2005MNRAS.362.1134B, doi:10.1111/j.1365-2966.2005.09359.x
- Bartusiak, Marcia (2000), Einstein's Unfinished Symphony: Listening to the Sounds of Space-Time, Berkley, ISBN 978-0-425-18620-6
- Begelman, Mitchell C.; Blandford, Roger D.; Rees, Martin J. (1984), “Theory of extragalactic radio sources”, Rev. Mod. Phys., 56 (2): 255–351, Bibcode:1984RvMP...56..255B, doi:10.1103/RevModPhys.56.255
- Beig, Robert; Chruściel, Piotr T. (2006), “Stationary black holes”, trong Francoise, J.-P.; Naber, G.; Tsou, T.S. (biên tập), Encyclopedia of Mathematical Physics, Volume 2, Elsevier, arXiv:gr-qc/0502041, Bibcode:2005gr.qc.....2041B, ISBN 0-12-512660-3
- Bekenstein, Jacob D. (1973), “Black Holes and Entropy”, Phys. Rev., D7 (8): 2333–2346, Bibcode:1973PhRvD...7.2333B, doi:10.1103/PhysRevD.7.2333
- Bekenstein, Jacob D. (1974), “Generalized Second Law of Thermodynamics in Black-Hole Physics”, Phys. Rev., D9 (12): 3292–3300, Bibcode:1974PhRvD...9.3292B, doi:10.1103/PhysRevD.9.3292
- Belinskii, V. A.; Khalatnikov, I. M.; Lifschitz, E. M. (1971), “Oscillatory approach to the singular point in relativistic cosmology”, Advances in Physics, 19 (80): 525–573, Bibcode:1970AdPhy..19..525B, doi:10.1080/00018737000101171; original paper in Russian: Belinsky, V. A.; Khalatnikov, I. M.; Lifshitz, E. M. (1970), “Колебательный Режим Приближения К Особой Точке В Релятивистской Космологии”, Uspekhi Fizicheskikh Nauk (Успехи Физических Наук), 102(3) (11): 463–500, Bibcode:1970UsFiN.102..463B
- Bennett, C. L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S. S.; Page, L.; Spergel, D. N. (2003), “First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results”, Astrophys. J. Suppl., 148 (1): 1–27, arXiv:astro-ph/0302207, Bibcode:2003ApJS..148....1B, doi:10.1086/377253
- Berger, Beverly K. (2002), “Numerical Approaches to Spacetime Singularities”, Living Rev. Relativity', 5, truy cập ngày 5 tháng 4 năm 2015
- Bergström, Lars; Goobar, Ariel (2003), Cosmology and Particle Astrophysics (ấn bản 2), Wiley & Sons, ISBN 3-540-43128-4
- Bertotti, Bruno; Ciufolini, Ignazio; Bender, Peter L. (1987), “New test of general relativity: Measurement of de Sitter geodetic precession rate for lunar perigee”, Physical Review Letters, 58 (11): 1062–1065, Bibcode:1987PhRvL..58.1062B, doi:10.1103/PhysRevLett.58.1062, PMID 10034329
- Bertotti, Bruno; Iess, L.; Tortora, P. (2003), “A test of general relativity using radio links with the Cassini spacecraft”, Nature, 425 (6956): 374–376, Bibcode:2003Natur.425..374B, doi:10.1038/nature01997, PMID 14508481
- Bertschinger, Edmund (1998), “Simulations of structure formation in the universe”, Annu. Rev. Astron. Astrophys., 36 (1): 599–654, Bibcode:1998ARA&A..36..599B, doi:10.1146/annurev.astro.36.1.599
- Birrell, N. D.; Davies, P. C. (1984), Quantum Fields in Curved Space, Cambridge University Press, ISBN 0-521-27858-9
- Blair, David; McNamara, Geoff (1997), Ripples on a Cosmic Sea. The Search for Gravitational Waves, Perseus, ISBN 0-7382-0137-5
- Blanchet, L.; Faye, G.; Iyer, B. R.; Sinha, S. (2008), The third post-Newtonian gravitational wave polarisations and associated spherical harmonic modes for inspiralling compact binaries in quasi-circular orbits, arXiv:0802.1249, Bibcode:2008CQGra..25p5003B, doi:10.1088/0264-9381/25/16/165003
- Blanchet, Luc (2006), “Gravitational Radiation from Post-Newtonian Sources and Inspiralling Compact Binaries”, Living Rev. Relativity, 9, truy cập ngày 5 tháng 4 năm 2015
- Blandford, R. D. (1987), “Astrophysical Black Holes”, trong Hawking, Stephen W.; Israel, Werner (biên tập), 300 Years of Gravitation, Cambridge University Press, tr. 277–329, ISBN 0-521-37976-8
- Börner, Gerhard (1993), The Early Universe. Facts and Fiction, Springer, ISBN 0-387-56729-1
- Brandenberger, Robert H. (2007), Conceptual Problems of Inflationary Cosmology and a New Approach to Cosmological Structure Formation, arXiv:hep-th/0701111, Bibcode:2008LNP...738..393B, doi:10.1007/978-3-540-74353-8_11
- Brans, C. H.; Dicke, R. H. (1961), “Mach's Principle and a Relativistic Theory of Gravitation”, Physical Review, 124 (3): 925–935, Bibcode:1961PhRv..124..925B, doi:10.1103/PhysRev.124.925
- Bridle, Sarah L.; Lahav, Ofer; Ostriker, Jeremiah P.; Steinhardt, Paul J. (2003), “Precision Cosmology? Not Just Yet”, Science, 299 (5612): 1532–1533, arXiv:astro-ph/0303180, Bibcode:2003Sci...299.1532B, doi:10.1126/science.1082158, PMID 12624255
- Bruhat, Yvonne (1962), “The Cauchy Problem”, trong Witten, Louis (biên tập), Gravitation: An Introduction to Current Research, Wiley, tr. 130, ISBN 978-1-114-29166-9
- Buchert, Thomas (2007), “Dark Energy from Structure—A Status Report”, General Relativity and Gravitation, 40 (2–3): 467–527, arXiv:0707.2153, Bibcode:2008GReGr..40..467B, doi:10.1007/s10714-007-0554-8
- Buras, R.; Rampp, M.; Janka, H.-Th.; Kifonidis, K. (2003), “Improved Models of Stellar Core Collapse and Still no Explosions: What is Missing?”, Phys. Rev. Lett., 90 (24): 241101, arXiv:astro-ph/0303171, Bibcode:2003PhRvL..90x1101B, doi:10.1103/PhysRevLett.90.241101, PMID 12857181
- Caldwell, Robert R. (2004), “Dark Energy”, Physics World, 17 (5): 37–42
- Carlip, Steven (2001), “Quantum Gravity: a Progress Report”, Rept. Prog. Phys., 64 (8): 885–942, arXiv:gr-qc/0108040, Bibcode:2001RPPh...64..885C, doi:10.1088/0034-4885/64/8/301
- Carroll, Bradley W.; Ostlie, Dale A. (1996), An Introduction to Modern Astrophysics, Addison-Wesley, ISBN 0-201-54730-9
- Carroll, Sean M. (2001), “The Cosmological Constant”, Living Rev. Relativity, 4, Bản gốc lưu trữ ngày 29 tháng 8 năm 2016, truy cập ngày 5 tháng 4 năm 2015
- Carter, Brandon (1979), “The general theory of the mechanical, electromagnetic and thermodynamic properties of black holes”, trong Hawking, S. W.; Israel, W. (biên tập), General Relativity, an Einstein Centenary Survey, Cambridge University Press, tr. 294–369 and 860–863, ISBN 0-521-29928-4
- Celotti, Annalisa; Miller, John C.; Sciama, Dennis W. (1999), “Astrophysical evidence for the existence of black holes”, Class. Quant. Grav., 16 (12A): A3–A21, arXiv:astro-ph/9912186, doi:10.1088/0264-9381/16/12A/301
- Chandrasekhar, Subrahmanyan (1983), The Mathematical Theory of Black Holes, Oxford University Press, ISBN 0-19-850370-9
- Charbonnel, C.; Primas, F. (2005), “The Lithium Content of the Galactic Halo Stars”, Astronomy & Astrophysics, 442 (3): 961–992, arXiv:astro-ph/0505247, Bibcode:2005A&A...442..961C, doi:10.1051/0004-6361:20042491
- Ciufolini, Ignazio; Pavlis, Erricos C. (2004), “A confirmation of the general relativistic prediction of the Lense-Thirring effect”, Nature, 431 (7011): 958–960, Bibcode:2004Natur.431..958C, doi:10.1038/nature03007, PMID 15496915
- Ciufolini, Ignazio; Pavlis, Erricos C.; Peron, R. (2006), “Determination of frame-dragging using Earth gravity models from CHAMP and GRACE”, New Astron., 11 (8): 527–550, Bibcode:2006NewA...11..527C, doi:10.1016/j.newast.2006.02.001
- Coc, A.; Vangioni‐Flam, Elisabeth; Descouvemont, Pierre; Adahchour, Abderrahim; Angulo, Carmen (2004), “Updated Big Bang Nucleosynthesis confronted to WMAP observations and to the Abundance of Light Elements”, Astrophysical Journal, 600 (2): 544–552, arXiv:astro-ph/0309480, Bibcode:2004ApJ...600..544C, doi:10.1086/380121
- Cutler, Curt; Thorne, Kip S. (2002), “An overview of gravitational wave sources”, trong Bishop, Nigel; Maharaj, Sunil D. (biên tập), Proceedings of 16th International Conference on General Relativity and Gravitation (GR16), World Scientific, arXiv:gr-qc/0204090, Bibcode:2002gr.qc.....4090C, ISBN 981-238-171-6
- Dalal, Neal; Holz, Daniel E.; Hughes, Scott A.; Jain, Bhuvnesh (2006), “Short GRB and binary black hole standard sirens as a probe of dark energy”, Phys.Rev., D74 (6): 063006, arXiv:astro-ph/0601275, Bibcode:2006PhRvD..74f3006D, doi:10.1103/PhysRevD.74.063006
- Danzmann, Karsten; Rüdiger, Albrecht (2003), “LISA Technology—Concepts, Status, Prospects” (PDF), Class. Quant. Grav., 20 (10): S1–S9, Bibcode:2003CQGra..20S...1D, doi:10.1088/0264-9381/20/10/301, Bản gốc (PDF) lưu trữ ngày 4 tháng 3 năm 2016, truy cập ngày 5 tháng 4 năm 2015
- Dirac, Paul (1996), General Theory of Relativity, Princeton University Press, ISBN 0-691-01146-X
- Donoghue, John F. (1995), “Introduction to the Effective Field Theory Description of Gravity”, trong Cornet, Fernando (biên tập), Effective Theories: Proceedings of the Advanced School, Almunecar, Spain, 26 June–ngày 1 tháng 7 năm 1995, Singapore: World Scientific, arXiv:gr-qc/9512024, Bibcode:1995gr.qc....12024D, ISBN 981-02-2908-9
- Duff, Michael (1996), “M-Theory (the Theory Formerly Known as Strings)”, Int. J. Mod. Phys., A11 (32): 5623–5641, arXiv:hep-th/9608117, Bibcode:1996IJMPA..11.5623D, doi:10.1142/S0217751X96002583
- Ehlers, Jürgen (1973), “Survey of general relativity theory”, trong Israel, Werner (biên tập), Relativity, Astrophysics and Cosmology, D. Reidel, tr. 1–125, ISBN 90-277-0369-8
- Ehlers, Jürgen; Falco, Emilio E.; Schneider, Peter (1992), Gravitational lenses, Springer, ISBN 3-540-66506-4
- Ehlers, Jürgen; Lämmerzahl, Claus biên tập (2006), Special Relativity—Will it Survive the Next 101 Years?, Springer, ISBN 3-540-34522-1
- Ehlers, Jürgen; Rindler, Wolfgang (1997), “Local and Global Light Bending in Einstein's and other Gravitational Theories”, General Relativity and Gravitation, 29 (4): 519–529, Bibcode:1997GReGr..29..519E, doi:10.1023/A:1018843001842
- Einstein, Albert (1907), “Über das Relativitätsprinzip und die aus demselben gezogene Folgerungen” (PDF), Jahrbuch der Radioaktivitaet und Elektronik, 4: 411, truy cập ngày 5 tháng 5 năm 2008
- Einstein, Albert (1915), “Die Feldgleichungen der Gravitation”, Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin: 844–847, Bản gốc lưu trữ ngày 27 tháng 10 năm 2016, truy cập ngày 12 tháng 9 năm 2006
- Einstein, Albert (1916), “Die Grundlage der allgemeinen Relativitätstheorie”, Annalen der Physik, 49, Bản gốc (PDF) lưu trữ ngày 29 tháng 8 năm 2006, truy cập ngày 3 tháng 9 năm 2006
- Einstein, Albert (1917), “Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie”, Sitzungsberichte der Preußischen Akademie der Wissenschaften: 142
- Ellis, George F R; van Elst, Henk (1999), “Cosmological models (Cargèse lectures 1998)”, trong Lachièze-Rey, Marc (biên tập), Theoretical and Observational Cosmology, Kluwer, tr. 1–116, arXiv:gr-qc/9812046, Bibcode:1999toc..conf....1E
- Everitt, C. W. F.; Buchman, S.; DeBra, D. B.; Keiser, G. M. (2001), “Gravity Probe B: Countdown to launch”, trong Lämmerzahl, F. W.; Everitt, and; Hehl, C. W. F. (biên tập), Gyros, Clocks, and Interferometers: Testing Relativistic Gravity in Space (Lecture Notes in Physics 562), Springer, tr. 52–82, ISBN 3-540-41236-0
- Everitt, C. W. F.; Parkinson, Bradford; Kahn, Bob (2007), The Gravity Probe B experiment. Post Flight Analysis—Final Report (Preface and Executive Summary) (PDF), Project Report: NASA, Stanford University and Lockheed Martin, truy cập ngày 5 tháng 8 năm 2007
- Falcke, Heino; Melia, Fulvio; Agol, Eric (2000), “Viewing the Shadow of the Black Hole at the Galactic Center”, Astrophysical Journal, 528 (1): L13–L16, arXiv:astro-ph/9912263, Bibcode:2000ApJ...528L..13F, doi:10.1086/312423, PMID 10587484
- Flanagan, Éanna É.; Hughes, Scott A. (2005), “The basics of gravitational wave theory”, New J.Phys., 7: 204, arXiv:gr-qc/0501041, Bibcode:2005NJPh....7..204F, doi:10.1088/1367-2630/7/1/204
- Font, José A. (2003), “Numerical Hydrodynamics in General Relativity”, Living Rev. Relativity, 6, truy cập ngày 5 tháng 4 năm 2015
- Fourès-Bruhat, Yvonne (1952), “Théoréme d'existence pour certains systémes d'équations aux derivées partielles non linéaires”, Acta Mathematica, 88 (1): 141–225, doi:10.1007/BF02392131
- Frauendiener, Jörg (2004), “Conformal Infinity”, Living Rev. Relativity, 7, truy cập ngày 5 tháng 4 năm 2015
- Friedrich, Helmut (2005), “Is general relativity `essentially understood'?”, Annalen Phys., 15 (1–2): 84–108, arXiv:gr-qc/0508016, Bibcode:2006AnP...518...84F, doi:10.1002/andp.200510173
- Futamase, T.; Itoh, Y. (2006), “The Post-Newtonian Approximation for Relativistic Compact Binaries”, Living Rev. Relativity, 10, truy cập ngày 5 tháng 4 năm 2015
- Gamow, George (1970), My World Line, Viking Press, ISBN 0-670-50376-2
- Garfinkle, David (2007), “Of singularities and breadmaking”, Einstein Online, Bản gốc lưu trữ ngày 15 tháng 1 năm 2015, truy cập ngày 3 tháng 8 năm 2007 Liên kết ngoài trong
|journal=(trợ giúp) - Geroch, Robert (1996). "Partial Differential Equations of Physics". arΧiv:gr-qc/9602055 [gr-qc].
- Giulini, Domenico (2005), Special Relativity: A First Encounter, Oxford University Press, ISBN 0-19-856746-4
- Giulini, Domenico (2006a), “Algebraic and Geometric Structures in Special Relativity”, trong Ehlers, Jürgen; Lämmerzahl, Claus (biên tập), Special Relativity—Will it Survive the Next 101 Years?, Springer, tr. 45–111, arXiv:math-ph/0602018, Bibcode:2006math.ph...2018G, ISBN 3-540-34522-1
- Giulini, Domenico (2006b), “Some remarks on the notions of general covariance and background independence”, trong Stamatescu, I. O. (biên tập), An assessment of current paradigms in the physics of fundamental interactions, Springer, arXiv:gr-qc/0603087, Bibcode:2007LNP...721..105G
- Gnedin, Nickolay Y. (2005), “Digitizing the Universe”, Nature, 435 (7042): 572–573, Bibcode:2005Natur.435..572G, doi:10.1038/435572a, PMID 15931201
- Goenner, Hubert F. M. (2004), “On the History of Unified Field Theories”, Living Rev. Relativity, 7, Bản gốc lưu trữ ngày 5 tháng 8 năm 2011, truy cập ngày 5 tháng 4 năm 2015
- Goroff, Marc H.; Sagnotti, Augusto (1985), “Quantum gravity at two loops”, Phys. Lett., 160B (1–3): 81–86, Bibcode:1985PhLB..160...81G, doi:10.1016/0370-2693(85)91470-4
- Gourgoulhon, Eric (2007). "3+1 Formalism and Bases of Numerical Relativity". arΧiv:gr-qc/0703035 [gr-qc].
- Gowdy, Robert H. (1971), “Gravitational Waves in Closed Universes”, Phys. Rev. Lett., 27 (12): 826–829, Bibcode:1971PhRvL..27..826G, doi:10.1103/PhysRevLett.27.826
- Gowdy, Robert H. (1974), “Vacuum spacetimes with two-parameter spacelike isometry groups and compact invariant hypersurfaces: Topologies and boundary conditions”, Ann. Phys. (N.Y.), 83 (1): 203–241, Bibcode:1974AnPhy..83..203G, doi:10.1016/0003-4916(74)90384-4
- Green, M. B.; Schwarz, J. H.; Witten, E. (1987), Superstring theory. Volume 1: Introduction, Cambridge University Press, ISBN 0-521-35752-7
- Greenstein, J. L.; Oke, J. B.; Shipman, H. L. (1971), “Effective Temperature, Radius, and Gravitational Redshift of Sirius B”, Astrophysical Journal, 169: 563, Bibcode:1971ApJ...169..563G, doi:10.1086/151174
- doi:10.1126/science.177.4044.166
Hoàn thành chú thích này - doi:10.1126/science.177.4044.168
Hoàn thành chú thích này - Havas, P. (1964), “Four-Dimensional Formulation of Newtonian Mechanics and Their Relation to the Special and the General Theory of Relativity”, Rev. Mod. Phys., 36 (4): 938–965, Bibcode:1964RvMP...36..938H, doi:10.1103/RevModPhys.36.938
- Hawking, Stephen W. (1966), “The occurrence of singularities in cosmology”, Proceedings of the Royal Society of London, A294 (1439): 511–521
- Hawking, S. W. (1975), “Particle Creation by Black Holes”, Communications in Mathematical Physics, 43 (3): 199–220, Bibcode:1975CMaPh..43..199H, doi:10.1007/BF02345020
- Hawking, Stephen W. (1987), “Quantum cosmology”, trong Hawking, Stephen W.; Israel, Werner (biên tập), 300 Years of Gravitation, Cambridge University Press, tr. 631–651, ISBN 0-521-37976-8
- Hawking, Stephen W.; Ellis, George F. R. (1973), The large scale structure of space-time, Cambridge University Press, ISBN 0-521-09906-4
- Heckmann, O. H. L.; Schücking, E. (1959), “Newtonsche und Einsteinsche Kosmologie”, trong Flügge, S. (biên tập), Encyclopedia of Physics, 53, tr. 489
- Heusler, Markus (1998), “Stationary Black Holes: Uniqueness and Beyond”, Living Rev. Relativity, 1, truy cập ngày 5 tháng 4 năm 2015
- Heusler, Markus (1996), Black Hole Uniqueness Theorems, Cambridge University Press, ISBN 0-521-56735-1
- Hey, Tony; Walters, Patrick (2003), The new quantum universe, Cambridge University Press, ISBN 0-521-56457-3
- Hough, Jim; Rowan, Sheila (2000), “Gravitational Wave Detection by Interferometry (Ground and Space)”, Living Rev. Relativity, 3, truy cập ngày 5 tháng 4 năm 2015
- Hubble, Edwin (1929), “A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae” (PDF), Proc. Nat. Acad. Sci., 15 (3): 168–173, Bibcode:1929PNAS...15..168H, doi:10.1073/pnas.15.3.168, PMC 522427, PMID 16577160
- Hulse, Russell A.; Taylor, Joseph H. (1975), “Discovery of a pulsar in a binary system”, Astrophys. J., 195: L51–L55, Bibcode:1975ApJ...195L..51H, doi:10.1086/181708
- Ibanez, L. E. (2000), “The second string (phenomenology) revolution”, Class. Quant. Grav., 17 (5): 1117–1128, arXiv:hep-ph/9911499, Bibcode:2000CQGra..17.1117I, doi:10.1088/0264-9381/17/5/321
- Iorio, L. (2009), “An Assessment of the Systematic Uncertainty in Present and Future Tests of the Lense-Thirring Effect with Satellite Laser Ranging”, Space Sci. Rev., 148 (1–4): 363, arXiv:0809.1373, Bibcode:2009SSRv..148..363I, doi:10.1007/s11214-008-9478-1
- Isham, Christopher J. (1994), “Prima facie questions in quantum gravity”, trong Ehlers, Jürgen; Friedrich, Helmut (biên tập), Canonical Gravity: From Classical to Quantum, Springer, ISBN 3-540-58339-4
- Israel, Werner (1971), “Event Horizons and Gravitational Collapse”, General Relativity and Gravitation, 2 (1): 53–59, Bibcode:1971GReGr...2...53I, doi:10.1007/BF02450518
- Israel, Werner (1987), “Dark stars: the evolution of an idea”, trong Hawking, Stephen W.; Israel, Werner (biên tập), 300 Years of Gravitation, Cambridge University Press, tr. 199–276, ISBN 0-521-37976-8
- Janssen, Michel (2005), “Of pots and holes: Einstein's bumpy road to general relativity”, Ann. Phys. (Leipzig), 14 (S1): 58–85, Bibcode:2005AnP...517S..58J, doi:10.1002/andp.200410130, Bản gốc (PDF) lưu trữ ngày 25 tháng 8 năm 2020, truy cập ngày 25 tháng 3 năm 2013
- Jaranowski, Piotr; Królak, Andrzej (2005), “Gravitational-Wave Data Analysis. Formalism and Sample Applications: The Gaussian Case”, Living Rev. Relativity, 8, truy cập ngày 5 tháng 4 năm 2015
- Kahn, Bob (1996–2012), Gravity Probe B Website, Stanford University, truy cập ngày 20 tháng 4 năm 2012
- Kahn, Bob (ngày 14 tháng 4 năm 2007), Was Einstein right? Scientists provide first public peek at Gravity Probe B results (Stanford University Press Release) (PDF), Stanford University News Service
- Kamionkowski, Marc; Kosowsky, Arthur; Stebbins, Albert (1997), “Statistics of Cosmic Microwave Background Polarization”, Phys. Rev., D55 (12): 7368–7388, arXiv:astro-ph/9611125, Bibcode:1997PhRvD..55.7368K, doi:10.1103/PhysRevD.55.7368
- Kennefick, Daniel (2005), “Astronomers Test General Relativity: Light-bending and the Solar Redshift”, trong Renn, Jürgen (biên tập), One hundred authors for Einstein, Wiley-VCH, tr. 178–181, ISBN 3-527-40574-7
- Kennefick, Daniel (2007), “Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition”, Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005, arXiv:0709.0685, Bibcode:2007arXiv0709.0685K
- Kenyon, I. R. (1990), General Relativity, Oxford University Press, ISBN 0-19-851996-6
- Kochanek, C.S.; Falco, E.E.; Impey, C.; Lehar, J. (2007), CASTLES Survey Website, Harvard-Smithsonian Center for Astrophysics, truy cập ngày 5 tháng 4 năm 2015
- Komar, Arthur (1959), “Covariant Conservation Laws in General Relativity”, Phys. Rev., 113 (3): 934–936, Bibcode:1959PhRv..113..934K, doi:10.1103/PhysRev.113.934
- Kramer, Michael (2004), Karshenboim, S. G.; Peik, E. (biên tập), “Astrophysics, Clocks and Fundamental Constants: Millisecond Pulsars as Tools of Fundamental Physics”, Lecture Notes in Physics, Springer, 648: 33–54, arXiv:astro-ph/0405178, Bibcode:2004LNP...648...33K, doi:10.1007/978-3-540-40991-5_3, ISBN 978-3-540-21967-5
- Kramer, M.; Stairs, I. H.; Manchester, R. N.; McLaughlin, M. A.; Lyne, A. G.; Ferdman, R. D.; Burgay, M.; Lorimer, D. R.; Possenti, A. (2006), “Tests of general relativity from timing the double pulsar”, Science, 314 (5796): 97–102, arXiv:astro-ph/0609417, Bibcode:2006Sci...314...97K, doi:10.1126/science.1132305, PMID 16973838
- Kraus, Ute (1998), “Light Deflection Near Neutron Stars”, Relativistic Astrophysics, Vieweg, tr. 66–81, ISBN 3-528-06909-0
- Kuchař, Karel (1973), “Canonical Quantization of Gravity”, trong Israel, Werner (biên tập), Relativity, Astrophysics and Cosmology, D. Reidel, tr. 237–288, ISBN 90-277-0369-8
- Künzle, H. P. (1972), “Galilei and Lorentz Structures on spacetime: comparison of the corresponding geometry and physics”, Ann. Inst. Henri Poincaré a, 17: 337–362
- Lahav, Ofer; Suto, Yasushi (2004), “Measuring our Universe from Galaxy Redshift Surveys”, Living Rev. Relativity, 7, truy cập ngày 5 tháng 4 năm 2015
- Landgraf, M.; Hechler, M.; Kemble, S. (2005), “Mission design for LISA Pathfinder”, Class. Quant. Grav., 22 (10): S487–S492, arXiv:gr-qc/0411071, Bibcode:2005CQGra..22S.487L, doi:10.1088/0264-9381/22/10/048
- Lehner, Luis (2001), “Numerical Relativity: A review”, Class. Quant. Grav., 18 (17): R25–R86, arXiv:gr-qc/0106072, Bibcode:2001CQGra..18R..25L, doi:10.1088/0264-9381/18/17/202
- Lehner, Luis (2002), Numerical Relativity: Status and Prospects, arXiv:gr-qc/0202055, Bibcode:2002grg..conf..210L, doi:10.1142/9789812776556_0010
- Linde, Andrei (1990), Particle Physics and Inflationary Cosmology, Harwood, arXiv:hep-th/0503203, Bibcode:2005hep.th....3203L, ISBN 3-7186-0489-2
- Linde, Andrei (2005), “Towards inflation in string theory”, J. Phys. Conf. Ser., 24: 151–160, arXiv:hep-th/0503195, Bibcode:2005JPhCS..24..151L, doi:10.1088/1742-6596/24/1/018
- Loll, Renate (1998), “Discrete Approaches to Quantum Gravity in Four Dimensions”, Living Rev. Relativity, 1, truy cập ngày 5 tháng 4 năm 2015
- Lovelock, David (1972), “The Four-Dimensionality of Space and the Einstein Tensor”, J. Math. Phys., 13 (6): 874–876, Bibcode:1972JMP....13..874L, doi:10.1063/1.1666069
- MacCallum, M. (2006), “Finding and using exact solutions of the Einstein equations”, trong Mornas, L.; Alonso, J. D. (biên tập), A Century of Relativity Physics (ERE05, the XXVIII Spanish Relativity Meeting), American Institute of Physics, arXiv:gr-qc/0601102, Bibcode:2006AIPC..841..129M, doi:10.1063/1.2218172
- Maddox, John (1998), What Remains To Be Discovered, Macmillan, ISBN 0-684-82292-X
- Mannheim, Philip D. (2006), “Alternatives to Dark Matter and Dark Energy”, Prog. Part. Nucl. Phys., 56 (2): 340–445, arXiv:astro-ph/0505266, Bibcode:2006PrPNP..56..340M, doi:10.1016/j.ppnp.2005.08.001
- Mather, J. C.; Cheng, E. S.; Cottingham, D. A.; Eplee, R. E.; Fixsen, D. J.; Hewagama, T.; Isaacman, R. B.; Jensen, K. A.; Meyer, S. S. (1994), “Measurement of the cosmic microwave spectrum by the COBE FIRAS instrument”, Astrophysical Journal, 420: 439–444, Bibcode:1994ApJ...420..439M, doi:10.1086/173574
- Mermin, N. David (2005), It's About Time. Understanding Einstein's Relativity, Princeton University Press, ISBN 0-691-12201-6
- Messiah, Albert (1999), Quantum Mechanics, Dover Publications, ISBN 0-486-40924-4
- Miller, Cole (2002), Stellar Structure and Evolution (Lecture notes for Astronomy 606), University of Maryland, truy cập ngày 25 tháng 7 năm 2007
- Misner, Charles W.; Thorne, Kip. S.; Wheeler, John A. (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0
- Møller, Christian (1952), The Theory of Relativity (ấn bản 3), Oxford University Press
- Narayan, Ramesh (2006), “Black holes in astrophysics”, New Journal of Physics, 7: 199, arXiv:gr-qc/0506078, Bibcode:2005NJPh....7..199N, doi:10.1088/1367-2630/7/1/199
- Narayan, Ramesh; Bartelmann, Matthias (1997). "Lectures on Gravitational Lensing". arΧiv:astro-ph/9606001 [astro-ph].
- Narlikar, Jayant V. (1993), Introduction to Cosmology, Cambridge University Press, ISBN 0-521-41250-1
- Nieto, Michael Martin (2006), “The quest to understand the Pioneer anomaly” (PDF), EurophysicsNews, 37 (6): 30–34
- Nordström, Gunnar (1918), “On the Energy of the Gravitational Field in Einstein's Theory”, Verhandl. Koninkl. Ned. Akad. Wetenschap., 26: 1238–1245
- Nordtvedt, Kenneth (2003). "Lunar Laser Ranging—a comprehensive probe of post-Newtonian gravity". arΧiv:gr-qc/0301024 [gr-qc].
- Norton, John D. (1985), “What was Einstein's principle of equivalence?” (PDF), Studies in History and Philosophy of Science, 16 (3): 203–246, doi:10.1016/0039-3681(85)90002-0, truy cập ngày 11 tháng 6 năm 2007
- Ohanian, Hans C.; Ruffini, Remo (1994), Gravitation and Spacetime, Ruffini, W. W. Norton & Company, ISBN 0-393-96501-5
- Olive, K. A.; Skillman, E. A. (2004), “A Realistic Determination of the Error on the Primordial Helium Abundance”, Astrophysical Journal, 617 (1): 29–49, arXiv:astro-ph/0405588, Bibcode:2004ApJ...617...29O, doi:10.1086/425170
- O'Meara, John M.; Tytler, David; Kirkman, David; Suzuki, Nao; Prochaska, Jason X.; Lubin, Dan; Wolfe, Arthur M. (2001), “The Deuterium to Hydrogen Abundance Ratio Towards a Fourth QSO: HS0105+1619”, Astrophysical Journal, 552 (2): 718–730, arXiv:astro-ph/0011179, Bibcode:2001ApJ...552..718O, doi:10.1086/320579
- Oppenheimer, J. Robert; Snyder, H. (1939), “On continued gravitational contraction”, Physical Review, 56 (5): 455–459, Bibcode:1939PhRv...56..455O, doi:10.1103/PhysRev.56.455
- Overbye, Dennis (1999), Lonely Hearts of the Cosmos: the story of the scientific quest for the secret of the Universe, Back Bay, ISBN 0-316-64896-5
- Pais, Abraham (1982), 'Subtle is the Lord...' The Science and life of Albert Einstein, Oxford University Press, ISBN 0-19-853907-X
- Peacock, John A. (1999), Cosmological Physics, Cambridge University Press, ISBN 0-521-41072-X
- Peebles, P. J. E. (1966), “Primordial Helium abundance and primordial fireball II”, Astrophysical Journal, 146: 542–552, Bibcode:1966ApJ...146..542P, doi:10.1086/148918
- Peebles, P. J. E. (1993), Principles of physical cosmology, Princeton University Press, ISBN 0-691-01933-9
- Peebles, P.J.E.; Schramm, D.N.; Turner, E.L.; Kron, R.G. (1991), “The case for the relativistic hot Big Bang cosmology”, Nature, 352 (6338): 769–776, Bibcode:1991Natur.352..769P, doi:10.1038/352769a0
- Penrose, Roger (1965), “Gravitational collapse and spacetime singularities”, Physical Review Letters, 14 (3): 57–59, Bibcode:1965PhRvL..14...57P, doi:10.1103/PhysRevLett.14.57
- Penrose, Roger (1969), “Gravitational collapse: the role of general relativity”, Rivista del Nuovo Cimento, 1: 252–276, Bibcode:1969NCimR...1..252P
- Penrose, Roger (2004), The Road to Reality, A. A. Knopf, ISBN 0-679-45443-8
- Penzias, A. A.; Wilson, R. W. (1965), “A measurement of excess antenna temperature at 4080 Mc/s”, Astrophysical Journal, 142: 419–421, Bibcode:1965ApJ...142..419P, doi:10.1086/148307
- Peskin, Michael E.; Schroeder, Daniel V. (1995), An Introduction to Quantum Field Theory, Addison-Wesley, ISBN 0-201-50397-2
- Peskin, Michael E. (2007), Dark Matter and Particle Physics, arXiv:0707.1536, Bibcode:2007JPSJ...76k1017P, doi:10.1143/JPSJ.76.111017
- Poisson, Eric (2004), “The Motion of Point Particles in Curved Spacetime”, Living Rev. Relativity, 7, Bản gốc lưu trữ ngày 13 tháng 9 năm 2015, truy cập ngày 5 tháng 4 năm 2015
- Poisson, Eric (2004), A Relativist's Toolkit. The Mathematics of Black-Hole Mechanics, Cambridge University Press, ISBN 0-521-83091-5
- Polchinski, Joseph (1998a), String Theory Vol. I: An Introduction to the Bosonic String, Cambridge University Press, ISBN 0-521-63303-6
- Polchinski, Joseph (1998b), String Theory Vol. II: Superstring Theory and Beyond, Cambridge University Press, ISBN 0-521-63304-4
- Pound, R. V.; Rebka, G. A. (1959), “Gravitational Red-Shift in Nuclear Resonance”, Physical Review Letters, 3 (9): 439–441, Bibcode:1959PhRvL...3..439P, doi:10.1103/PhysRevLett.3.439
- Pound, R. V.; Rebka, G. A. (1960), “Apparent weight of photons”, Phys. Rev. Lett., 4 (7): 337–341, Bibcode:1960PhRvL...4..337P, doi:10.1103/PhysRevLett.4.337
- Pound, R. V.; Snider, J. L. (1964), “Effect of Gravity on Nuclear Resonance”, Phys. Rev. Lett., 13 (18): 539–540, Bibcode:1964PhRvL..13..539P, doi:10.1103/PhysRevLett.13.539
- Ramond, Pierre (1990), Field Theory: A Modern Primer, Addison-Wesley, ISBN 0-201-54611-6
- Rees, Martin (1966), “Appearance of Relativistically Expanding Radio Sources”, Nature, 211 (5048): 468–470, Bibcode:1966Natur.211..468R, doi:10.1038/211468a0
- Reissner, H. (1916), “Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie”, Annalen der Physik, 355 (9): 106–120, Bibcode:1916AnP...355..106R, doi:10.1002/andp.19163550905
- Remillard, Ronald A.; Lin, Dacheng; Cooper, Randall L.; Narayan, Ramesh (2006), “The Rates of Type I X-Ray Bursts from Transients Observed with RXTE: Evidence for Black Hole Event Horizons”, Astrophysical Journal, 646 (1): 407–419, arXiv:astro-ph/0509758, Bibcode:2006ApJ...646..407R, doi:10.1086/504862
- Renn, Jürgen biên tập (2007), The Genesis of General Relativity (4 Volumes), Dordrecht: Springer, ISBN 1-4020-3999-9
- Renn, Jürgen biên tập (2005), Albert Einstein—Chief Engineer of the Universe: Einstein's Life and Work in Context, Berlin: Wiley-VCH, ISBN 3-527-40571-2
- Reula, Oscar A. (1998), “Hyperbolic Methods for Einstein's Equations”, Living Rev. Relativity, 1, truy cập ngày 5 tháng 4 năm 2015
- Rindler, Wolfgang (2001), Relativity. Special, General and Cosmological, Oxford University Press, ISBN 0-19-850836-0
- Rindler, Wolfgang (1991), Introduction to Special Relativity, Clarendon Press, Oxford, ISBN 0-19-853952-5
- Robson, Ian (1996), Active galactic nuclei, John Wiley, ISBN 0-471-95853-0
- Roulet, E.; Mollerach, S. (1997), “Microlensing”, Physics Reports, 279 (2): 67–118, arXiv:astro-ph/9603119, Bibcode:1997PhR...279...67R, doi:10.1016/S0370-1573(96)00020-8
- Rovelli, Carlo (2000). "Notes for a brief history of quantum gravity". arΧiv:gr-qc/0006061 [gr-qc].
- Rovelli, Carlo (1998), “Loop Quantum Gravity”, Living Rev. Relativity, 1, Bản gốc lưu trữ ngày 27 tháng 10 năm 2009, truy cập ngày 5 tháng 4 năm 2015
- Schäfer, Gerhard (2004), “Gravitomagnetic Effects”, General Relativity and Gravitation, 36 (10): 2223–2235, arXiv:gr-qc/0407116, Bibcode:2004GReGr..36.2223S, doi:10.1023/B:GERG.0000046180.97877.32
- Schödel, R.; Ott, T.; Genzel, R.; Eckart, A.; Mouawad, N.; Alexander, T. (2003), “Stellar Dynamics in the Central Arcsecond of Our Galaxy”, Astrophysical Journal, 596 (2): 1015–1034, arXiv:astro-ph/0306214, Bibcode:2003ApJ...596.1015S, doi:10.1086/378122
- Schutz, Bernard F. (1985), A first course in general relativity, Cambridge University Press, ISBN 0-521-27703-5
- Schutz, Bernard F. (2001), “Gravitational radiation”, trong Murdin, Paul (biên tập), Encyclopedia of Astronomy and Astrophysics, Grove's Dictionaries, ISBN 1-56159-268-4
- Schutz, Bernard F. (2003), Gravity from the ground up, Cambridge University Press, ISBN 0-521-45506-5
- Schwarz, John H. (2007), String Theory: Progress and Problems, arXiv:hep-th/0702219, Bibcode:2007PThPS.170..214S, doi:10.1143/PTPS.170.214
- Schwarzschild, Karl (1916a), “Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie”, Sitzungsber. Preuss. Akad. D. Wiss.: 189–196
- Schwarzschild, Karl (1916b), “Über das Gravitationsfeld eines Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie”, Sitzungsber. Preuss. Akad. D. Wiss.: 424–434
- Seidel, Edward (1998), “Numerical Relativity: Towards Simulations of 3D Black Hole Coalescence”, trong Narlikar, J. V.; Dadhich, N. (biên tập), Gravitation and Relativity: At the turn of the millennium (Proceedings of the GR-15 Conference, held at IUCAA, Pune, India, December 16–21, 1997), IUCAA, arXiv:gr-qc/9806088, Bibcode:1998gr.qc.....6088S, ISBN 81-900378-3-8
- Seljak, Uros̆; Zaldarriaga, Matias (1997), “Signature of Gravity Waves in the Polarization of the Microwave Background”, Phys. Rev. Lett., 78 (11): 2054–2057, arXiv:astro-ph/9609169, Bibcode:1997PhRvL..78.2054S, doi:10.1103/PhysRevLett.78.2054
- Shapiro, S. S.; Davis, J. L.; Lebach, D. E.; Gregory, J. S. (2004), “Measurement of the solar gravitational deflection of radio waves using geodetic very-long-baseline interferometry data, 1979–1999”, Phys. Rev. Lett., 92 (12): 121101, Bibcode:2004PhRvL..92l1101S, doi:10.1103/PhysRevLett.92.121101, PMID 15089661
- Shapiro, Irwin I. (1964), “Fourth test of general relativity”, Phys. Rev. Lett., 13 (26): 789–791, Bibcode:1964PhRvL..13..789S, doi:10.1103/PhysRevLett.13.789
- Shapiro, I. I.; Pettengill, Gordon; Ash, Michael; Stone, Melvin; Smith, William; Ingalls, Richard; Brockelman, Richard (1968), “Fourth test of general relativity: preliminary results”, Phys. Rev. Lett., 20 (22): 1265–1269, Bibcode:1968PhRvL..20.1265S, doi:10.1103/PhysRevLett.20.1265
- Singh, Simon (2004), Big Bang: The Origin of the Universe, Fourth Estate, ISBN 0-00-715251-5
- Sorkin, Rafael D. (2005), “Causal Sets: Discrete Gravity”, trong Gomberoff, Andres; Marolf, Donald (biên tập), Lectures on Quantum Gravity, Springer, arXiv:gr-qc/0309009, Bibcode:2003gr.qc.....9009S, ISBN 0-387-23995-2
- Sorkin, Rafael D. (1997), “Forks in the Road, on the Way to Quantum Gravity”, Int. J. Theor. Phys., 36 (12): 2759–2781, arXiv:gr-qc/9706002, Bibcode:1997IJTP...36.2759S, doi:10.1007/BF02435709
- Spergel, D. N.; Verde, L.; Peiris, H. V.; Komatsu, E.; Nolta, M. R.; Bennett, C. L.; Halpern, M.; Hinshaw, G.; Jarosik, N. (2003), “First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters”, Astrophys. J. Suppl., 148 (1): 175–194, arXiv:astro-ph/0302209, Bibcode:2003ApJS..148..175S, doi:10.1086/377226
- Spergel, D. N.; Bean, R.; Doré, O.; Nolta, M. R.; Bennett, C. L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; Komatsu, E. (2007), “Wilkinson Microwave Anisotropy Probe (WMAP) Three Year Results: Implications for Cosmology”, Astrophysical Journal Supplement, 170 (2): 377–408, arXiv:astro-ph/0603449, Bibcode:2007ApJS..170..377S, doi:10.1086/513700
- Springel, Volker; White, Simon D. M.; Jenkins, Adrian; Frenk, Carlos S.; Yoshida, Naoki; Gao, Liang; Navarro, Julio; Thacker, Robert; Croton, Darren (2005), “Simulations of the formation, evolution and clustering of galaxies and quasars”, Nature, 435 (7042): 629–636, arXiv:astro-ph/0504097, Bibcode:2005Natur.435..629S, doi:10.1038/nature03597, PMID 15931216
- Stairs, Ingrid H. (2003), “Testing General Relativity with Pulsar Timing”, Living Rev. Relativity, 6, Bản gốc lưu trữ ngày 12 tháng 4 năm 2013, truy cập ngày 5 tháng 4 năm 2015
- Stephani, H.; Kramer, D.; MacCallum, M.; Hoenselaers, C.; Herlt, E. (2003), Exact Solutions of Einstein's Field Equations (ấn bản 2), Cambridge University Press, ISBN 0-521-46136-7
- Synge, J. L. (1972), Relativity: The Special Theory, North-Holland Publishing Company, ISBN 0-7204-0064-3
- Szabados, László B. (2004), “Quasi-Local Energy-Momentum and Angular Momentum in GR”, Living Rev. Relativity, 7, truy cập ngày 5 tháng 4 năm 2015
- Taylor, Joseph H. (1994), “Binary pulsars and relativistic gravity”, Rev. Mod. Phys., 66 (3): 711–719, Bibcode:1994RvMP...66..711T, doi:10.1103/RevModPhys.66.711
- Thiemann, Thomas (2006). "Loop Quantum Gravity: An Inside View". arΧiv:hep-th/0608210.
- Thiemann, Thomas (2003), “Lectures on Loop Quantum Gravity”, Lect. Notes Phys., 631: 41–135
- Thorne, Kip S. (1972), “Nonspherical Gravitational Collapse—A Short Review”, trong Klauder, J. (biên tập), Magic without Magic, W. H. Freeman, tr. 231–258
- Thorne, Kip S. (1994), Black Holes and Time Warps: Einstein's Outrageous Legacy, W W Norton & Company, ISBN 0-393-31276-3
- Thorne, Kip S. (1995), Gravitational radiation, arXiv:gr-qc/9506086, Bibcode:1995pnac.conf..160T, ISBN 0-521-36853-7
- Townsend, Paul K. (1997). "Black Holes (Lecture notes)". arΧiv:gr-qc/9707012 [gr-qc].
- Townsend, Paul K. (1996). "Four Lectures on M-Theory". arΧiv:hep-th/9612121.
- Traschen, Jenny (2000), “An Introduction to Black Hole Evaporation”, trong Bytsenko, A.; Williams, F. (biên tập), Mathematical Methods of Physics (Proceedings of the 1999 Londrina Winter School), World Scientific, arXiv:gr-qc/0010055, Bibcode:2000mmp..conf..180T
- Trautman, Andrzej (2006), “Einstein-Cartan theory”, trong Francoise, J.-P.; Naber, G. L.; Tsou, S. T. (biên tập), Encyclopedia of Mathematical Physics, Vol. 2, Elsevier, tr. 189–195, arXiv:gr-qc/0606062, Bibcode:2006gr.qc.....6062T
- Unruh, W. G. (1976), “Notes on Black Hole Evaporation”, Phys. Rev. D, 14 (4): 870–892, Bibcode:1976PhRvD..14..870U, doi:10.1103/PhysRevD.14.870
- Valtonen, M. J.; Lehto, H. J.; Nilsson, K.; Heidt, J.; Takalo, L. O.; Sillanpää, A.; Villforth, C.; Kidger, M.; Poyner, G. (2008), “A massive binary black-hole system in OJ 287 and a test of general relativity”, Nature, 452 (7189): 851–853, arXiv:0809.1280, Bibcode:2008Natur.452..851V, doi:10.1038/nature06896, PMID 18421348
- Wald, Robert M. (1975), “On Particle Creation by Black Holes”, Commun. Math. Phys., 45 (3): 9–34, Bibcode:1975CMaPh..45....9W, doi:10.1007/BF01609863
- Wald, Robert M. (1984), General Relativity, University of Chicago Press, ISBN 0-226-87033-2
- Wald, Robert M. (1994), Quantum field theory in curved spacetime and black hole thermodynamics, University of Chicago Press, ISBN 0-226-87027-8
- Wald, Robert M. (2001), “The Thermodynamics of Black Holes”, Living Rev. Relativity, 4, Bản gốc lưu trữ ngày 28 tháng 2 năm 2011, truy cập ngày 5 tháng 4 năm 2015
- Walsh, D.; Carswell, R. F.; Weymann, R. J. (1979), “0957 + 561 A, B: twin quasistellar objects or gravitational lens?”, Nature, 279 (5712): 381, Bibcode:1979Natur.279..381W, doi:10.1038/279381a0, PMID 16068158
- Wambsganss, Joachim (1998), “Gravitational Lensing in Astronomy”, Living Rev. Relativity, 1, truy cập ngày 5 tháng 4 năm 2015
- Weinberg, Steven (1972), Gravitation and Cosmology, John Wiley, ISBN 0-471-92567-5
- Weinberg, Steven (1995), The Quantum Theory of Fields I: Foundations, Cambridge University Press, ISBN 0-521-55001-7
- Weinberg, Steven (1996), The Quantum Theory of Fields II: Modern Applications, Cambridge University Press, ISBN 0-521-55002-5
- Weinberg, Steven (2000), The Quantum Theory of Fields III: Supersymmetry, Cambridge University Press, ISBN 0-521-66000-9
- Weisberg, Joel M.; Taylor, Joseph H. (2003), “The Relativistic Binary Pulsar B1913+16"”, trong Bailes, M.; Nice, D. J.; Thorsett, S. E. (biên tập), Proceedings of "Radio Pulsars," Chania, Crete, August, 2002, ASP Conference Series
- Weiss, Achim (2006), “Elements of the past: Big Bang Nucleosynthesis and observation”, Einstein Online, Max Planck Institute for Gravitational Physics, Bản gốc lưu trữ ngày 29 tháng 7 năm 2010, truy cập ngày 5 tháng 4 năm 2015 Liên kết ngoài trong
|journal=(trợ giúp) - Wheeler, John A. (1990), A Journey Into Gravity and Spacetime, Scientific American Library, San Francisco: W. H. Freeman, ISBN 0-7167-6034-7
- Will, Clifford M. (1993), Theory and experiment in gravitational physics, Cambridge University Press, ISBN 0-521-43973-6
- Will, Clifford M. (2006), “The Confrontation between General Relativity and Experiment”, Living Rev. Relativity, Bản gốc lưu trữ ngày 19 tháng 3 năm 2015, truy cập ngày 5 tháng 4 năm 2015
- Zwiebach, Barton (2004), A First Course in String Theory, Cambridge University Press, ISBN 0-521-83143-1
Đọc thêm[sửa | sửa mã nguồn]
Sách phổ thông[sửa | sửa mã nguồn]
- Geroch, Robert (1981). General Relativity from A to B. Chicago: Nhà xuất bản Đại học Chicago. ISBN 0-226-28864-1.
- Wald, Robert M. (1992). Space, Time, and Gravity: the Theory of the Big Bang and Black Holes. Chicago: Nhà xuất bản Đại học Chicago. ISBN 0-226-87029-4.
- Thorne, Kip S. (1995). Black Holes and Time Warps: Einstein's Outrageous Legacy. Thành phố New York: W. W. Norton. ISBN 0-393-31276-3.
Sách giáo khoa[sửa | sửa mã nguồn]
Sách căn bản[sửa | sửa mã nguồn]
- Hughston, L.; Tod, K. P. (1991). Introduction to General Relativity. Cambridge: Nhà xuất bản Đại học Cambridge. ISBN 0-521-33943-X.
- d'Inverno, Ray (1992). Introducing Einstein's Relativity. Oxford: Nhà xuất bản Đại học Oxford. ISBN 0-19-859686-3.
- Schutz, Bernard F. (1985). A First Course in General Relativity. Cambridge: Nhà xuất bản Đại học Cambridge. ISBN 0-521-27703-5.
- Stephani, Hans (1990). General Relativity: An Introduction to the Theory of the Gravitational Field. Cambridge: Nhà xuất bản Đại học Cambridge. ISBN 0-521-37941-5.
- Ohanian, Hans C.; Ruffini, Remo (1994). Gravitation and Spacetime. Thành phố New York: W. W. Norton. ISBN 0-393-96501-5.
- Taylor, Edwin F.; Wheeler, John Archibald (2000). Exploring Black Holes: Introduction to General Relativity. Addison Wesley. ISBN 0-201-38423-X.
Sách nâng cao[sửa | sửa mã nguồn]
- Carroll, Sean M. (2004). Spacetime and Geometry: An Introduction to General Relativity. San Francisco: Addison-Wesley. ISBN 0-8053-8732-3.
- Landau, L. D.; Lifschitz, E. F. (1980). The Classical Theory of Fields. Luân Đôn: Butterworth-Heinemann. ISBN 0-7506-2768-9.
- Misner, Charles; Thorne, Kip S.; Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 0-7167-0344-0.
- Weinberg, Steven (1972). Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. New York: John Wiley & Sons. ISBN 0-471-92567-5.
- Wald, Robert M. (1984). General Relativity. Chicago: Nhà xuất bản Đại học Chicago. ISBN 0-226-87033-2.
Sách chuyên đề[sửa | sửa mã nguồn]
- Lightman, Alan P.; Press, William H.; Teukolsky, Saul A. (1975). Problem Book in Relativity and Gravitation. Princeton, New Jersey: Nhà xuất bản Đại học Princeton. ISBN 0-691-08162-X.
- Poisson, Eric (2004). A Relativist's Toolkit: The Mathematics of Black Hole Mechanics. Cambridge: Nhà xuất bản Đại học Cambridge. ISBN 0-521-83091-5.
- Stewart, John (1993). Advanced General Relativity. Cambridge: Nhà xuất bản Đại học Cambridge. ISBN 0-521-44946-4.
- De Felice, F.; Clarke, C. J. (1992). Relativity on Curved Manifolds. Cambridge: Nhà xuất bản Đại học Cambridge. ISBN 0-521-42908-0.
- Hawking, Stephen W.; Ellis, George F.R. (1973). The Large Scale Structure of Space-Time. Nhà xuất bản Đại học Cambridge. ISBN 978-0-521-09906-6.
Liên kết ngoài[sửa | sửa mã nguồn]
| Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Thuyết tương đối rộng. |
| Wikisource có văn bản gốc Anh ngữ liên quan với bài: |
| Wikisource có văn bản gốc Anh ngữ liên quan với bài: |
- Hawking, Steven (2001). Vũ trụ trong một vỏ hạt: Lược sử về thuyết tương đối. Bantam. ISBN 0-553-71449-X. Bản dịch tiếng Việt của Dạ Trạch.
- Einstein Online Lưu trữ 2014-06-01 tại Wayback Machine – Articles on a variety of aspects of relativistic physics for a general audience; hosted by the Max Planck Institute for Gravitational Physics
- NCSA Spacetime Wrinkles Lưu trữ 2015-03-27 tại Wayback Machine – produced by the numerical relativity group at the NCSA, with an elementary introduction to general relativity
- Bài giảng trực tuyến, sách điện tử
- Einstein's General Theory of Relativity by Leonard Susskind's Modern Physics lectures. Recorded ngày 22 tháng 9 năm 2008 at Stanford University
- Series of lectures on General Relativity given in 2006 at the Institut Henri Poincaré (introductory courses and advanced ones).
- General Relativity Tutorials Lưu trữ 2007-07-07 tại Wayback Machine by John Baez
- Brown, Kevin. “Reflections on relativity”. Mathpages.com. Truy cập 25 tháng 3 năm 2013.
- Carroll, Sean M. “Lecture Notes on General Relativity”. Truy cập 25 tháng 3 năm 2013.
- Moor, Rafi. “Understanding General Relativity”. Truy cập 25 tháng 3 năm 2013.
- Waner, Stefan. “Introduction to Differential Geometry and General Relativity” (PDF). Truy cập ngày 13 tháng 9 năm 2015.




































































